種類
有形數可依照該數能排成的形狀分成:
多邊形數、多面體數、中心多邊形數、中心多面體數、星數、角錐數、角柱數、多胞體數.......等。
例子
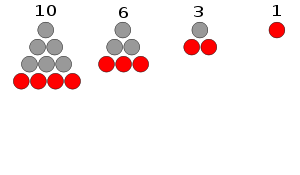
有形數能排成三角形的有形數
前17個三角形數是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153……（OEIS中的數列A000217）
梯形數
能排成梯形的有形數
前15個梯形數為2,7,15,26,40,57,77,100,126,155,187,222,260,301,345......（OEIS中的數列A005449）
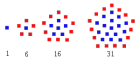中心五邊形數中心五邊形數
排成從中心延伸出去的五邊形
前15項的中心五邊形數為1,6,16,31,51,76,106,141,181,226,276,331,391,456,526......（OEIS中的數列A005891）.
四角錐的有形數能堆成四角錐的有形數
前13個四角錐數是1,5,14,30,55,91,140,204,285,385,506,650,819......（OEIS中的數列A000330）.
六角星數
能排成六角星的有形數
前13個六角星數是1,13,37,73,121,181,253,337,433,541,661,793,937......（OEIS中的數列A003154）
趣味數學
| 趣味數學以帶有強烈的遊戲色彩知名於世。歐拉就是通過對bridge-crossing之謎的分析打下了拓撲學的基礎。萊布尼茨也寫到過他在獨自玩插棍遊戲時分析問題的樂趣。希爾伯特證明了切割幾何圖形中的許多重要定理。馮·紐曼奠基了博弈論。最受大眾歡迎的計算機遊戲—生命是英國著名數學家康威發明的。愛因斯坦也收藏了整整一書架關於數學遊戲和數學謎的書。 |
