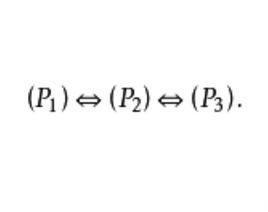基本介紹
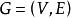 完美圖
完美圖我們已經知道,對任一個圖,有如下一些基本參數:
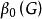 完美圖
完美圖點無關數,即最大點無關集的點數;
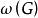 完美圖
完美圖團數,即最大團的點數;
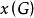 完美圖
完美圖點色數;
還有另一個參數:
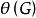 完美圖
完美圖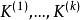 完美圖
完美圖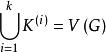 完美圖
完美圖團覆蓋數,即這樣的最小的k,使G中存在k個團,有。
 完美圖
完美圖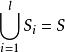 完美圖
完美圖 完美圖
完美圖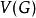 完美圖
完美圖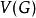 完美圖
完美圖如果我們給了一個集合S的一個子集族,使,則稱覆蓋了S,利用“覆蓋”的語言,那么點色數就是覆蓋所需要的點無關集的最小個數;而團覆蓋數就是覆蓋所需要的團的最小個數。
以上這些參數之間有著緊密的聯繫。若G 是G的補圖,則有
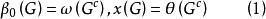 完美圖
完美圖這是因為在G與G 中,點無關集和團是一一對應的.。此外,顯然有
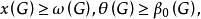 完美圖
完美圖這是因為任一個團和任一個點無關集最多有一個公共點。
1960年Berge引進了完美圖的概念。
稱圖G是x完美圖,如果
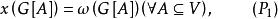 完美圖
完美圖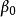 完美圖
完美圖稱圖G是完美圖,如果
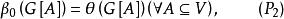 完美圖
完美圖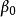 完美圖
完美圖若圖G既是x完美圖,又是完美圖,則稱G是 完美圖 。
相關性質定理
1961年,Berge提出了如下猜想 :
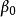 完美圖
完美圖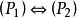 完美圖
完美圖一個圖是完美的充分必要條件是它為x完美圖(或完美圖),即。
1972年,Lovász,Fulkerson相繼獨立地證明了這個猜想。
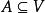 完美圖
完美圖因為對任意的,有
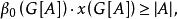 完美圖
完美圖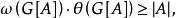 完美圖
完美圖所以當G滿足(P)或(P)時,顯然也滿足
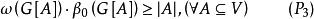 完美圖
完美圖由(1)推知:
 完美圖
完美圖G滿足(P)G 滿足(P);
 完美圖
完美圖G滿足(P)G 滿足(Ps),
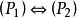 完美圖
完美圖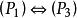 完美圖
完美圖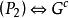 完美圖
完美圖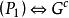 完美圖
完美圖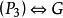 完美圖
完美圖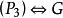 完美圖
完美圖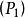 完美圖
完美圖所以假如我們能夠證明,則G滿足滿足滿足滿足滿足,從而就證明了。
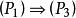 完美圖
完美圖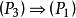 完美圖
完美圖因已知,所以證明上述Berge猜想的關鍵是去證明。
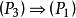 完美圖
完美圖現在我們給出的證明。
首先引入圖上的一種運算——倍點運算。
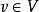 完美圖
完美圖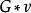 完美圖
完美圖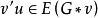 完美圖
完美圖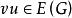 完美圖
完美圖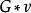 完美圖
完美圖對任意的,用表示這樣的一個圖:在G中增加一個新點v',並且若且唯若,我們說是由G通過倍點運算得到的。
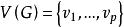 完美圖
完美圖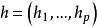 完美圖
完美圖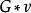 完美圖
完美圖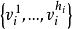 完美圖
完美圖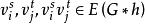 完美圖
完美圖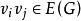 完美圖
完美圖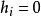 完美圖
完美圖 完美圖
完美圖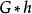 完美圖
完美圖設,設是任一非負整數向量,以表示這樣的一個圖: 用點無關集代替v,對任意的若且唯若,當某個時,則意味著從G中丟去,因此,對任意的(0,1)向量h,與G的生成子圖對應。
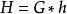 完美圖
完美圖引理1 設,則
(1)若G滿足(P),則H滿足(P);
(2)若G滿足(P),則H滿足(P)。
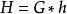 完美圖
完美圖引理2(Fulkerson,1971;Lovász,1972)設G滿足(P),令,那么由G滿足(P)可推出日滿足(P)。
引理3(Lovász,1972)若G滿足(P),則G滿足(P)。
由引理3,就可推得
定理 對任意圖G,
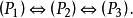 完美圖
完美圖推論1 圖G是完美圖若且唯若G 是完美圖。
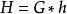 完美圖
完美圖推論2 圖G是完美圖若且唯若是完美圖。
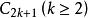 完美圖
完美圖由前面我們已經知道,若G或G 包含一個生成子圖,則G不是完美圖。
Berge關於完美圖的第二個猜想(強完美圖猜想)是
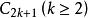 完美圖
完美圖猜想 若G或G 不含生成子圖,則G是完美圖。
迄今已知這個猜想對許多圖類是成立的,如三角圖 。