證明方法
方法1
從被證共圓的四點中先選出三點作一圓,然後證另一點也在這個圓周上,若能證明這一點,即可肯定這四點共圓.方法2
 圖A:四點共圓的圖片
圖A:四點共圓的圖片方法3
把被證共圓的四點連成四邊形,若能證明其對角互補或能證明其一個外角等於其鄰補角的內對角時,即可肯定這四點共圓.方法4
把被證共圓的四點兩兩連成相交的兩條線段,若能證明它們各自被交點分成的兩線段之積相等,即可肯定這四點共圓(相交弦定理的逆定理);或把被證共圓的四點兩兩連結並延長相交的兩線段,若能證明自交點至一線段兩個端點所成的兩線段之積等於自交點至另一線段兩端點所成的兩線段之積,即可肯定這四點也共圓.(割線定理的逆定理)方法5
證被證共圓的點到某一定點的距離都相等,從而確定它們共圓.即連成的四邊形三邊中垂線有交點,可肯定這四點共圓.上述五種基本方法中的每一種的根據,就是產生四點共圓的一種原因,因此當要求證四點共圓的問題時,首先就要根據命題的條件,並結合圖形的特點,在這五種基本方法中選擇一種證法,給予證明.
判定與性質:
圓內接四邊形的對角和為180°,並且任何一個外角都等於它的內對角。
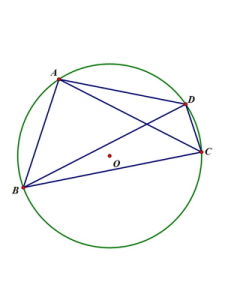
【如圖A:四點共圓的圖片】
圖A:四點共圓的圖片
四邊形ABCD內接於圓O,延長AB和DC交至E,過點E作圓O的切線EF,AC、BD交於P,則有:
(1)∠A+∠C=π,∠B+∠D=π(即圖中∠DAB+∠DCB=π,∠ABC+∠ADC=π)
(2)∠DBC=∠DAC(同弧所對的圓周角相等)。
(3)∠ADE=∠CBE(外角等於內對角,可通過(1)、(2)得到)
(4)△ABP∽△DCP(兩三角形三個內角對應相等,可有(2)得到)
(5)AP*CP=BP*DP(相交弦定理)
(6)EB*EA=EC*ED(割線定理)
(7)EF^2=EB*EA=EC*ED(切割線定理)
(8)AB*CD+AD*CB=AC*BD(托勒密定理)
說明:切割線定理,割線定理,相交弦定理統稱圓冪定理
其他定理:弦切角定理
定理
判定定理
方法1把被證共圓的四個點連成共底邊的兩個三角形,且兩三角形都在這底邊的同側,若能證明其頂角相等,從而即可肯定這四點共圓.(可以說成:若線段同側二點到線段兩端點連線夾角相等,那么這二點和線段二端點四點共圓)
方法2把被證共圓的四點連成四邊形,若能證明其對角互補或能證明其一個外角等於其鄰補角的內對角時,即可肯定這四點共圓.
(可以說成:若平面上四點連成四邊形的對角互補或一個外角等於其內對角。那么這四點共圓)
托勒密定理
若ABCD四點共圓(ABCD按順序都在同一個圓上),那么AB*DC+BC*AD=AC*BD。例題:證明對於任意正整數n都存在n個點使得所有點間兩兩距離為整數。
解答:歸納法。我們用歸納法證明一個更強的定理:對於任意n都存在n個點使得所有點間兩兩距離為整數,且這n個點共圓,並且有兩點是一條直徑的兩端。n=1,n=2很輕鬆。當n=3時,一個邊長為整數的勾股三角形即可:比如說邊長為3,4,5的三角形。我們發現這樣的三個點共圓,邊長最長的邊是一條直徑。假設對於n大於等於3成立,我們來證明n+1。假設直徑為r(整數)。找一個不跟已存在的以這個直徑為斜邊的三角形相似的一個整數勾股三角形ABC(邊長a<b<c)。把原來的圓擴大到原來的c倍,並把一個邊長為ra<rb<rc的三角形放進去,使得rc邊和放大後的直徑重合。這個三角形在圓上面對應了第n+1個點,記為P。於是根據Ptolomy定理,P和已存在的所有點的距離都是一個有理數。(考慮P,這個點Q和直徑兩端的四個點,這四點共圓,於是PQ是一個有理數因為Ptolomy定理里的其它數都是整數。)引入一個新的點P增加了n個新的有理數距離,記這n個有理數的最大公分母為M。最後只需要把這個新的圖擴大到原來的M倍即可。歸納法成立,故有這個命題。
反證法證明
現就“若平面上四點連成四邊形的對角互補。那么這個四點共圓”證明如下(其它畫個證明圖如後)已知:四邊形ABCD中,∠A+∠C=180°
求證:四邊形ABCD內接於一個圓(A,B,C,D四點共圓)
證明:用反證法
過A,B,D作圓O,假設C不在圓O上,點C在圓外或圓內,
若點C在圓外,設BC交圓O於C’,連結DC’,根據圓內接四邊形的性質得∠A+∠DC’B=180°,
∵∠A+∠C=180°∴∠DC’B=∠C
這與三角形外角定理矛盾,故C不可能在圓外。類似地可證C不可能在圓內。
∴C在圓O上,也即A,B,C,D四點共圓。