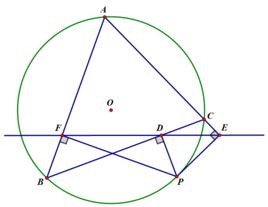
定理定義
相關的結果有:
(1)稱三角形的 垂心 為H。西姆松線和PH的交點為線段PH的中點,且這點在 九點圓 上。
(2)兩點的西姆松線的 交角 等於該兩點的 圓周角 。
(3)若兩個三角形的外接圓相同,這外接 圓 上的一點P對應兩者的西姆松線的交角,跟P的位置無關。
(4)從一點向 三角形 的三邊所引垂線的垂足共線的 充要條件 是該點落在三角形的 外接圓 上。
驗證推導
證明一:△ABC外接圓上有點P,且PE⊥AC於E,PF⊥BC於F,PD⊥AB於D,分別連FE、FD、BP、CP.
易證P、B、D、F和P、F、C、E分別共圓,(四點共圓)
在PBDF圓內,∠DBP+∠DFP=180度,在ABPC圓內∠ABP+∠ACP =180度,
∴∠DFP=∠ACP ①,在PFCE圓內 ∠PFE=∠PCE
② 而∠ACP+∠PCE=180°
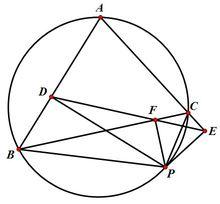 證明一
證明一③ ∴∠DFP+∠PFE=180° ④ 即D、F、E共線. 反之,當D、F、E共線時,由④→②→③→①可見A、B、P、C共圓.
證明二:
如圖,若L、M、N三點共線,連結BP,CP,則因PL垂直於
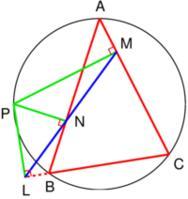 西姆松定理
西姆松定理BC,PM垂直於AC,PN垂直於AB,有B、L、P、N和P、M、C、
L分別四點共圓,有
∠NBP = ∠NLP
= ∠MLP= ∠MCP.
故A、B、P、C四點共圓。
若A、P、B、C四點共圓,則
∠NBP= ∠MCP。因PL垂直於BC,PM垂直於AC,PN垂直於AB,
有B、L、P、N和P、M、C、L四點共圓,有
∠NBP = ∠NLP
= ∠MCP
= ∠MLP.
故L、M、N三點共線。
相關性質的證明
M為線段PH的中點連AH延長線交圓於G。
1.M為線段PH的中點連AH延長線交圓於G。
證明:連PG交西姆松線與R,BC於Q
如圖連其他相關線段
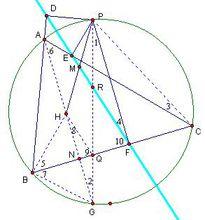 西姆松定理
西姆松定理AH⊥BC,PF⊥BC==>AG//PF==>∠1=∠2A.G.C.P共圓==>∠2=∠3
PE⊥AC,PF⊥BC==>P.E.F.C共圓==>∠3=∠4
==>∠1=∠4
PF⊥BC
==>PR=RQ
BH⊥AC,AH⊥BC==>∠5=∠6
A.B.G.C共圓==>∠6=∠7
==>∠5=∠7
AG⊥BC==>BC垂直平分GH
==>∠8=∠2=∠4
∠8+∠9=90,∠10+∠4=90==>∠9=∠10
==>HQ//DF
==>PM=MH
2.平分點在九點圓上。
證明:如圖:設O,G,H 分別為三角形ABC的外心,重心和垂心。
則O是,確定九點圓的中點三角形XYZ的垂心,而G還是它的重心。
那么三角形XYZ的外心 O1, 也在同一直線上,並且
HG/GO=GO/GO1=2,所以O1是OH的中點。
三角形ABC和三角形XYZ位似,那么它們的外接圓也位似。兩個圓的圓心都在OH上,並且兩圓半徑比為1:2
所以G是三角形ABC外接圓和三角形XYZ外接圓(九點圓)的"反"位似中心(相似點在位似中心的兩邊),H 是"正"位似中心(相似點在位似中心的同一邊)。
所以H到三角形ABC的外接圓上的連線中點必在三角形DEF的外接圓上。