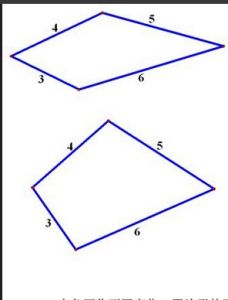
四邊形的定義
凸四邊形
作出一邊所在直線，其餘各邊均在其同側。平行四邊形(包括：普通平行四邊形,矩形,菱形,正方形)。
梯形(包括:普通梯形,直角梯形,等腰梯形)。
凸四邊形的內角和和外角和均為360度。
凹四邊形
作出一邊所在直線，其餘各邊有些在其異側。不做重點研究。
依次連線四邊形各邊中點所得的四邊形稱為中點四邊形。不管原四邊形的形狀怎樣改變，中點四邊形的形狀始終是平行四邊形。中點四邊形的形狀取決於原四邊形的對角線。若原四邊形的對角線垂直，則中點四邊形為矩形；若原四邊形的對角線相等，則中點四邊形為菱形；若原四邊形的對角線既垂直又相等，則中點四邊形為正方形。平行四邊形定義
兩組對邊分別平行的四邊形叫做平行四邊形(parallelogram)。
平行四邊形性質（簡述為“平行四邊形的兩組對邊分別相等”）
（2）如果一個四邊形是平行四邊形，那么這個四邊形的兩組對角分別相等。
（簡述為“平行四邊形的兩組對角分別相等”）（3）如果一個四邊形是平行四邊形，那么這個四邊形的鄰角互補
（簡述為“平行四邊形的鄰角互補”）
（4）夾在兩條平行線間的平行線段相等。
（5）如果一個四邊形是平行四邊形，那么這個四邊形的兩條對角線互相平分。
（簡述為“平行四邊形的對角線互相平分”）
判定
（1）如果一個四邊形的兩組對邊分別相等，那么這個四邊形是平行四邊形。（簡述為“兩組對邊分別相等的四邊形是平行四邊形”）
（2）如果一個四邊形的一組對邊平行且相等，那么這個四邊形是平行四邊形。
（簡述為“一組對邊平行且相等的四邊形是平行四邊形”）
（3）如果一個四邊形的兩條對角線互相平分，那么這個四邊形是平行四邊形。
（簡述為“對角線互相平分的四邊形是平行四邊形”）
（4）如果一個四邊形的兩組對角分別相等，那么這個四邊形是平行四邊形。
（簡述為“兩組對角分別相等的四邊形是平行四邊形”
（5）如果一個四邊形的兩組對邊分別平行，那么這個四邊形是平行四邊形。
（簡述為“兩組對邊分別平行的四邊形是平行四邊形”）
面積
平行四邊形的面積公式：底×高 用“h”表示高，“a”表示底，“S”表示平行四邊形面積，則S=ah
周長
平行四邊形的周長=2×兩鄰邊的和，用“a”、“b”表示兩鄰邊，“C”表示平行四邊形的周長，則C=2（a+b）
矩形
定義
有一個角是直角的平行四邊形叫做矩形(rectangle).
矩形性質
①矩形的四個角都是直角；②矩形的對角線相等.
注意：矩形也具有平行四邊形的一切性質.
判定
①有一個角是直角的平行四邊形叫做矩形；②四個角都相等的四邊形是矩形；
③對角線相等的平行四邊形是矩形；
④對角線相等且互相平分的四邊形是矩形；
⑤有三個角是直角的四邊形是矩形.
面積
設矩形的兩條鄰邊長分別為a,b，則面積為ab.周長
設矩形的兩條鄰邊長分別為a,b，則周長為(2a+2b).菱形
定義
有一組鄰邊相等的平行四邊形叫做菱形(rhombus).
菱形性質
①菱形的四條邊都相等；②菱形的對角線互相垂直，並且每一條對角線平分一組對角.
注意：菱形也具有平行四邊形的一切性質.
判定
①有一組鄰邊相等的平行四邊形是菱形；②四條邊都相等的四邊形是菱形；
③對角線互相垂直的平行四邊形是菱形
④有一條對角線平分一組對角的平行四邊形是菱形
⑤對角線互相垂直且平分的四邊形是菱形
面積
①對角線乘積的一半（只要是對角線互相垂直的四邊形都可用）；②設菱形的邊長為a,一個夾角為x°，則面積公式是:S=a^2·sinx
周長
菱形周長=邊長×4 用“a”表示菱形的邊長，“C”表示菱形的周長，則C=4a
正方形
定義
有一組鄰邊相等並且有一角是直角的平行四邊形叫做正方形(square)。
正方形性質
①正方形的四個角都是直角，四條邊都相等；②正方形的兩條對角線相等，並且互相垂直平分，每條對角線平分一組對角。
判定
因為正方形具有平行四邊形、矩形、菱形的一切性質，所以判定正方形有四個途徑：①有一組鄰邊相等的矩形是正方形。
②有一個角是直角的菱形是正方形。
③兩條對角線相等，且互相垂直平分的四邊形是正方形。
④兩條對角線相等，且互相垂直的平行四邊形是正方形。
面積
①正方形面積=邊長的平方 S=a×a（S表示正方形的面積，a表示正方形的邊長）。
②對角線乘積的一半。周長
正方形周長=邊長×4 用“a”表示正方形的邊長，“C”表示正方形的周長，則C=4a梯形及特殊梯形
定義
梯形：一組對邊平行而另一組對邊不平行的四邊形叫做梯形(trapezium)（一組對邊平行且不相等的四邊形叫做梯形）。等腰梯形：兩腰相等的梯形叫做等腰梯形(isosceles trapezium)。
梯形直角梯形：一腰垂直於底的梯形叫做直角梯形。
等腰梯形的性質
1、等腰梯形兩腰相等、兩底平行；2、等腰梯形在同一底上的兩個內角相等；
3、等腰梯形的對角線相等(可能垂直）；
4、等腰梯形是軸對稱圖形，它只有一條對稱軸，一底的垂直平分線是它的對稱軸。
等腰梯形的判定
1、兩腰相等的梯形是等腰梯形。2、在同一底上的兩個角相等的梯形是等腰梯形。
3、對角線相等的梯形是等腰梯形。
面積
1、梯形的面積公式：（上底+下底）×高÷22、梯形面積=梯形中位線×高
周長
梯形的周長=上底+下底+腰+腰 用“a”、“b”、“c”、“d”分別表示梯形的上底、下底、兩腰，“C”表示梯形的周長則c=a+b+c+d
圓內接四邊形
定義
四邊形的四個頂點均在同一個圓上的四邊形叫做圓內接四邊形。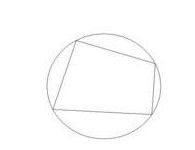
圓內接四邊形性質
1、圓內接四邊形的對角互補。2、圓內接四邊形的任意一個外角等於它的內對角。
3、圓的內接凸四邊形兩對對邊乘積的和等於兩條對角線的乘積。（托勒密定理）
判定
如果一個四邊形的對角互補，那么這個四邊形的四個頂點在同一個圓上。面積
圓內接四邊形面積S=√[(p-a)(p-b)(p-c)(p-d)]。（a,b,c,d為四邊形的四邊長,其中P=(a+b+c+d)/2對角線垂直四邊形
定義
對角線互相垂直的四邊形。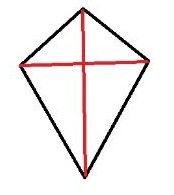
對角線垂直的四邊形性質
四邊形面積等於兩條對角線的積的一半。例：四邊形ABCD中，AC⊥BD ，則S□ABCD=1/2·AC·BD
