簡述
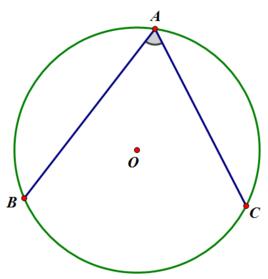
圓周角(angle of circumference)是指頂點在圓上，且兩邊和圓相交的角。在同圓或等圓中，兩圓周角相等，則其所對的弦(或弧)也相等；反之，等弧所對的圓周角相等。而等弦所對圓周角相等或相補，圓周角的度數等於它所對弧的度數的一半。
對於一個圓周角，角的內部必然夾了一段圓弧，通常把圓周角說成是這一弧上的圓周角，或說這一弧所對的圓周角。另外，角的外部也有一段圓弧，我們還把圓周角說成是這一弧所含的圓周角。
定理推論
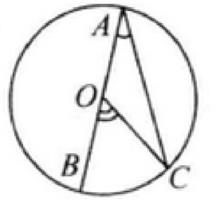
圖一圓周角定理:在同圓或等圓中，同弧或等弧所對的圓周角都等於這條弧所對的圓心角的一半。證明：
情況一：先考慮一種特殊情況——圓心O在圓周角∠BAC的邊上（如圖一）.由三角形外角性質有
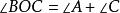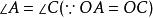圓周角
圓周角但
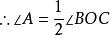圓周角情況二：如果圓心O在圓周角∠BAC的內部（如圖二），可以劃歸為前一種類型——引直徑AD。∠BAD，∠CAD都是圓心在邊上的圓周角。則有：
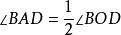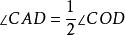圓周角
圓周角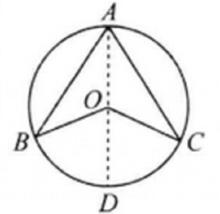
圖二兩式相加即得
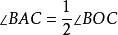圓周角. 情況三：如果圓心O在圓周角∠BAC的外部（如圖三），仍可以 劃歸為前一種類型——引直徑AD。這時∠BAD，∠CAD都是圓心在邊上的圓周角。則有：
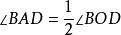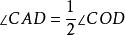圓周角 圓周角兩式相減即得
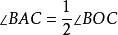圓周角這樣，即完成了定理的證明。圓周角定理有如下推論：
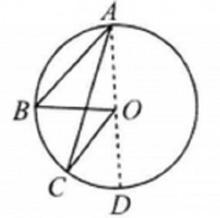圖三推論1：同弧或等弧所對的圓周角相等；同圓或等圓中，相等的圓周角所對的弧也相等．聯繫圓心角、弧、弦、弦心距之間的關係．對於在推理論證及相關計算中有著廣泛的用途．
推論2：半圓(或直徑)所對的圓周角是直角，90°的圓周角所對的弦是直徑。
推論3：如果三角形一邊上的中線等於這邊的一半，那么這個三角形是直角三角形。這兩個推論是判定直角或直角三角形的又一依據，為在圓中確定直角，構造垂直關係，創造了條件，因此它是圓中一個很重要的性質。
命題證明
命題1: 在圓中作弦MN，於直線MN同側取點A、B、C，使點A、B、C分別在圓內、上、外，將點A、B、C分別與點M、N連結，則有∠A>∠B>∠C。
命題2: 頂點在圓外的角（兩邊與圓相交）的度數等於其所截兩弧度數差的一半；頂點在圓內的角（兩邊與圓相交）的度數等於其及其對頂角所截弧度數和的一半。
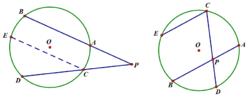圓周角證明：如圖，過C作CE//AB，交圓於E，
則有∠P=∠DCE，弧AC=弧BE（圓中兩平行弦所夾弧相等）
而∠DCE的度數等於弧DE的一半，弧DE=弧BD－弧BE=弧BD－弧AC
所以∠DCE的度數等於“弧BD－弧AC”的一半
即“頂點在圓外的角（兩邊與圓相交）的度數等於其所截兩弧度數差的一半”
另外也可以連線BC，則∠P=∠BCD－∠B
∠BCD的度數等於弧BD的度數的一半
∠B的度數等於弧AC的度數的一半
同樣得“頂點在圓外的角（兩邊與圓相交）的度數等於其所截兩弧度數差的一半”
圓內角的證明完全類似：
過C作CE//AB，交圓於E，
則有∠APC=∠C，弧AC=弧BE（圓中兩平行弦所夾弧相等）
而∠C的度數等於弧DE的一半，
弧DE=弧BD+弧BE=弧BD+弧AC
所以∠APC的度數等於“弧BD+弧AC”的一半
即“頂點在圓內的角（兩邊與圓相交）的度數等於其所截兩弧度數和的一半”
另外也可以連線BC進行證明
