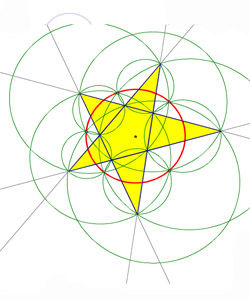
內容及證明
在任意五角星AJEIDHCGBF中,△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圓順次相交的交點分別是K、O、N、M、L。
求證:K、O、N、M、L五點共圓。
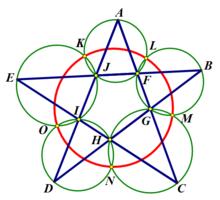 五點共圓
五點共圓證明:連線CN、HN、KN、IN、MN、MG、ML、LF、LK、KA
∵∠ACN+∠AIN=∠NHD+∠AIN=∠NID+∠AIN=180° ∴A、I、N、C四點共圓
同理A、K、I、C四點共圓從而A、C、N、K四點共圓
∴∠GMN=∠GCN=∠ACN=180°-∠AKN又∠LMG=180°-∠LFG=∠LFA=∠LKA
∴∠LMN=∠LMG+∠GMN=∠LKA+(180°-∠AKN)
∴∠LMN+∠LKN=∠LKA+(180°-∠AKN)+∠LKN=180° 故K、L、M、N四點共圓
同理可證O、L、M、N四點共圓
∴K、O、N、M、L五點共圓
證畢。
背景
據報導,2000年12月20日,江澤民主席出席澳門回歸祖國一周年慶典活動期間,在參觀濠江中學時向該校師生出了一道求證“五點共圓”的平面幾何題:“假設:任意一個星形,五個三角形,外接圓交於五點。求證:這五點共圓。”
江主席說:“我也當過中學教師,所以我對教師感到特別親切。中學教學,要教好語文、歷史、地理,數學也應該重視。”“我把這道題出給濠江中學,是要說明:一個人總要有鑽研精神。”
香港科技大學數學系副教授李健賢說,三角幾何能提供邏輯及觀察力的訓練,可鍛鍊分析能力。不過,香港的數學教育注重運算,較少要求學生去處理這類幾何難題。香港只有少數大學生能解答江主席出的這道幾何題。香港喇沙中學的一名會考十優生陳貴祥表示,老師曾講授過這道考題的基本理論,但他並未做過與這道考題相關的習作。
據說,數學大師丘成桐也用了半小時才悟出此難題答案。
2000年12月28日,澳門濠江中學師生給江主席寄出了答案。兩天后,江主席請澳門特區行政長官何厚鏵轉交了給濠江中學師生的回信。
江主席出的這道平面幾何題用規範的數學語言表述是這樣的:在任意五角星AJEIDHCGBF中,△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圓順次相交的交點分別為K、O、N、M、L。求證:K、O、N、M、L五點共圓