詞語概念
基本信息
 命題
命題 拼音:mìngtí
英譯 :assign a topic
基本解釋
[assign a topic] 出 題目命題作文
◎ 命題 mìngtí
(1) [proposition]∶邏輯學指表達判斷的語言形式,由系詞把主詞和賓詞聯繫而成
(2) [problem]∶數學或物理中要進行某種說明的 問題
命題:二等分一直線
引證解釋
1.指所確定的詩文等的主旨。宋王禹偁《贈別鮑秀才序》:“公出文數十章,即進士 鮑生 之作也。命題立意,殆非常人。”
2.擬題;出題目。
明王鏊《震澤長語·經傳》:“古人作詩,必自命題。”
《二十年目睹之怪現狀》第七三回:“有一回,書院裡官課, 歷城縣 親自到院 命題考試。”
曹靖華《飛花集·談散文》:“而我的座上客既不象威風凜凜的大主考,命題作文,也不帶任何框框。”
這次高考的作文是命題作文。
3.所出的題目; 題目。
清孫枝蔚《賦得東渚雨今足呈潞安司理李吉六》詩序:“司理公下車後分題試各邑士之能詩者,余適在家兄署中,欣聞體恤屬吏及惠愛農民之意,正圖形諸歌詠,因見命題,輒不揣荒陋,勉作二律,附邑士之末。”
《新華文摘》1981年第7期:“但在思想以至氣質上,他依然是一位 檢察官,因此我才用了現在的命題。”
4.邏輯學名詞。表達判斷的句子。
毛澤東《新民主主義論》四:“‘ 中國革命是世界革命的一部分’,這一正確的命題,還是在一九二四年至一九二七年的 中國 第一次大革命時期,就提出了的。”一說凡陳述句所表達的意義為命題,被斷定了的命題為判斷。
5.數學概念
(1)國中數學中命題的概念為:“判斷一件事情的語句”;高中教材中定義為:“可以判斷真假的語句”。
(2).一般地,在數學中,我們把用語言、符號或式子表達的,可以判斷真假的陳述句叫做命題。其中判斷為真的語句叫做真命題,判斷為假的語句叫做假命題。
(3).“若p,則q”形式的命題中p叫做命題的題設或條件,q叫做命題的結論。
基本含義
命題的分類
 命題
命題 亞里士多德以後的邏輯學家,如泰奧弗拉斯多、麥加拉學派和斯多阿學派的邏輯學家,以及中世紀的邏輯學家等,又對包含有命題聯結詞"或者"、"並且"、"如果,則"等的複合命題進行了不斷的探討,從而豐富了邏輯學關於命題的 學說。
康德的分類
I.康德根據他的範疇理論對判斷作了分類。這個分類對後世的 影響很大。康德對判斷的分類主要有4個方面:①量,包括全稱、特稱、單稱三種判斷;②質,包括肯定、否定、無限(所有S是非P)這幾種判斷;③關係,有直言(兩概念間的關係)、假言(兩判斷間的關係)、選言(若干判斷間的關係)判斷。④模態,有或(概)然、實然、確然幾種判斷。康德所謂的模態,是指認識的程度。他認為組成假言判斷、選言判斷的判斷,都是或然的。傳統邏輯的分類
19世紀下半葉歐洲邏輯讀本對命題的分類不盡一致。大體說來,按關係即按命題主謂項之間的關係分,有直言命題、假言命題(後件主謂項的聯繫以前件為條件)和選言命題(謂項之間對主項有選擇關係)。從質的角度分,有肯定命題和否定命題。從量的角度分,有全稱命題,包括單稱命題、普遍命題(凡S是P)和特稱命題。這些讀本還討論了其他一些關於數量多少的命題,如涉及"多數"、"少數"之類的命題;並認為,"多數 S是P"等值於"少數S不是P","少數 S是P"等值於"多數S不是P"。因此,從"所有S是P"推不出"多數S是P",也推不出"少數S是P"。這些傳統邏輯讀本在 討論選言命題時,也往往論及聯言命題、分離命題(非A並且非B)等。另外,還有一類可解析命題也是常常提到的。在這類命題中,有一種叫區別命題,其形式為"只有S才是P";還有一種叫除外命題,其形式為"除是M的S外每個S是P"。
形式分析
現代邏輯對命題形式的分析
由於推理的有效性只與推理的前提和結論的形式有關,而與作為前提和結論的命題的具體內容無關。因此,在經典的二值邏輯里,命題可以只看成真(記為T)和假(記為F)兩種,並統稱為真值。它以p,q,...為命題變項,其變域為{T,F}。最基本的推理,僅僅與命題 聯結詞有關。自然語言中最常見的命題聯結詞有:"或者"、"並且"、"如果,則"、"並非"等,把這些聯結詞抽象為真值聯結詞,分別記為:"∨",表示析取詞;"∧",表示合取詞;"→" ,表示蘊涵詞;"風",表示等值詞,相當於"若且唯若";"填",表示否定詞。真值聯結詞與命題變項的一定的組合,就是複合命題形式的抽象,它們實質上是一種真值函項。真值函項的域和值域都是 {T,F},這些函項把一個或一組真值映射到一個並且只有一個真值上。這樣,分別由∨,∧,→,風,填這 5個真值聯結詞都可以用真值函項定義。聯結詞也可以在命題形式中多次出現,以構成較為複雜的形式。對命題形式的進一步分析,要深入到最簡單命題內部的非命題成分。在現代邏輯中,類似"蘇格拉底是人"這樣的命題,被認為是最簡單的命題。若以s代表"蘇格拉底",以M代表"人",該類命題就可記為M(s),這表示某一個體s具有性質R。推廣來說,最簡單的命題的形式為F(x),可讀作論域中的個體x具有性質F;較為複雜的形式可以有填G(x,y)),可讀作論域中的個體x,y)之間具有關係G。在這裡,x,y),...稱為個體變項;F,G,...稱為謂詞變項,而F是一元的,G是二元的。n個個體變項之間有n元關係H就記為H(x,...,xn-1)。若以L代表"處在流動的狀態",而"每個事物都處在流動的 狀態"就可記為風xL(x),這可讀為:對論域裡所有個體x 而言,x 處在流動的狀態。其中,風x 叫做全稱量詞,風是全稱量詞符號。若以B代表"尚未被人認識的",則"至少有一個東西是尚未被人認識的",可記為 ヨxB(x),讀作論域中至少有一個體 x,x 尚未被人認識。在這裡ヨx 是存在量詞,而ヨ是存在量詞符號。"不存在一個最大的實數", 可表示為 填ヨy)風x(y)>x),其論域為實數。"任意兩實數之間至少有一個實數",可表示為風x風y)ヨz(x
四種命題
 命題
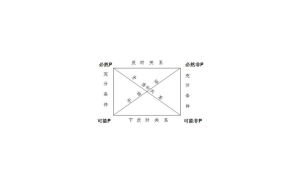
命題 2.對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的條件的否定和結論的否定,那么這兩個命題叫做互否命題,其中一個命題叫做原命題,另外一個命題叫做原命題的否命題。
3.對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的結論的否定和條件的否定,那么這兩個命題叫做互為逆否命題,其中一個命題叫做原命題,另外一個命題叫做原命題的逆否命題。
相互關係
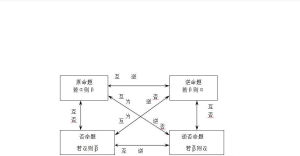
1.四種命題的相互關係:原命題與逆命題互逆,否命題與原命題互否,原命題與逆否命題 相互逆否,逆命題與否命題相互逆否,逆命題與逆否命題互否,逆否命題與否命題互逆。2.四種命題的真假關係:(1)兩個命題互為逆否命題,它們有相同的真假性。(2)兩個命題為互逆命題或互否命題,它們的真假性沒有關係(原命題與逆否命題同真同假,逆命題與否命題同真同假)
命題關係
1、能夠判斷真假的陳述句叫做命題,正確的命題叫做 真命題,錯誤的命題叫做 假命題。2、“若p,則q”形式的命題中p叫做命題的條件,q叫做命題的結論。
3、命題的分類:
① 原命題:一個命題的本身稱之為原命題,如:若x>1,則f(x)=(x-1)^2單調遞增。
② 逆命題:將原命題的條件和結論顛倒的新命題,如:若f(x)=(x-1)^2單調遞增,則x>1。
③ 否命題:將原命題的條件和結論全否定的新命題,但不改變條件和結論的順序,如:若x《1,則f(x)=(x-1)^2不單調遞增。
④ 逆否命題:將原命題的條件和結論顛倒,然後再將條件和結論全否定的新命題,如:若f(x)=(x-1)^2不單調遞增,則x《1。
4、命題的否定
命題的否定是只將命題的結論否定的新命題,這與否命題不同。
5、4種命題及命題的否定的真假性關係
原命題和逆否命題等價,否命題和逆命題等價,命題的否定與原命題的真假性相反。
命題條件
充分和必要條件
1.“若p,則q”為真命題,叫做由p推出q,記作p=>q,並且說p是q的充分條件,q是p的必要 條件。2.“若p,則q”為假命題,叫做由p推不出q,記作p≠>q,並且說p不是q的充分條件(或p是q的非充分條件),q不是p的必要條件(或q是p的非必要條件)。
充要條件
如果既有p=>q,又有q=>p,就記作pq,並且說p是q的充分必要條件(或q是p的充分必要條件),簡稱充要條件。幾何命題
 命題
命題 1. 在一個已知有限直線上作一個等邊三角形。
2. 由一個已知點(作為端點)作一線段等於已知線段。
3. 已知兩條不相等的線段,試由大的上邊截取一條 線段使它等於另外一條。
4. 如果兩個三角形有兩邊分別等於兩邊,而且這些相等的線段所夾的角相等,那么,它們的底邊等於底邊,三角形全等於三角形,而且其餘的角等於其餘的角,即那等邊所對的角。
5. 在等腰三角形中,兩底角彼此相等;並且,若向下延長兩腰,則在底以下的兩角也彼此相等。
6. 如果在一個三角形中,有兩角彼此相等,則等角所對的邊也彼此相等。
7. 在已知線段上(從它的兩個端點)作出相交於一點的二線段,則不可能在該線段(從它的兩個 端點)的同側作出相交於另一點的另二條線段,使得作出的二線段分別等於前面二線段。即每個交點到相同端點的線段相等。
8. 如果兩個三角形的一個有兩邊分別等於另一個的兩邊,並且一個的底等於另一個的底,則夾在等邊中間的角也相等。
9. 二等分一個己知直線角。
10. 二等分已知有限直線。
11. 由已知直線上一已知點作一直線和已知直線成 直角。
12. 由已知無限直線外一已知點作該直線的垂線。
13. 一條直線和另一條直線所交成的鄰角,或者是兩個直角或者它們等於兩個直角的和。
14. 如果過任意直線上點有兩條直線不在這一 直線的同側,且和直線所成鄰角和等於二直角,則這兩條直線在同一直線上。
15. 如果兩直線相交,則它們交成的對頂角相等。
16. 在任意的三角形中,若延長一邊,則外角大於任何一個內對角。
17. 在任何三角形中,任何兩角之和小於兩直角。
18. 在任何三角形中,大邊對大角。
19. 在任何三角形中,大角對大邊。
20. 在任何三角形中,任意兩邊之和大於第三邊。
21. 如果由三角形的一條邊的兩個端點作相交於三角形內的兩條線段,由交點到兩端點的線段的和小於三角形其餘兩邊的 和。但是,其夾角大於三角形的頂角。
22. 試由分別等於已知三條線段的三條線段作一個三角形:在這樣的三條已知線段中,任二條線段之和必須大於另外一條線段。
23. 在已知直線和它上面一點,作一個直線角等於己知直線角。
24. 如果兩個三角形中,一個的兩條邊分別與另一個的兩條邊相等,且一個的夾角大於另一個的夾角,則夾角大的所對的邊也較大。
25. 如果在兩個三角形中,一個的兩條邊分別等於另一個的兩條邊,則第三邊較大的所對的角也較大。
26. 如果在兩個三角形中,一個的兩個角分別等於另一個的兩個角,而且一邊等於另一個的一邊。即或者這邊是等角的夾邊,或者是等角的對邊。則它們的其他的邊也等於其他的邊,且其他的角也等於其他的角。
27. 如果一直線和兩直線相交所成的錯 角彼此相等,則這二直線互相平行。
28. 如果一直線和二直線相交所成的同位角相等,或者同旁內角的和等於二直角,則二直線互相平行。
29. 一條直線與兩條平行直線相交,則所成的內錯角相等,同位角相等,且同旁內角的和等於二直角。
30. 一些直線平行於同一條直線,則它們也互相 平行。
31. 過一已知點作一直線平行於已知直線。
32. 在任意三角形中,如果延長一邊,則外角等於二內對角的和,而且三角形的三個內角的和等於二直角。
33. 在同一方向(分別)連線相等且平行的線段(的端點),它們自身也相等且平行。
34. 在平行四邊形面片中,對邊 相等,對角相等且對角線二等分其面片。
35. 在同底上且在相同兩平行線之間的平行四邊形彼此相等。
36. 在等底上且在相同二平行線之間的平行四邊形彼此相等。
37. 在同底上且在相同二平行線之間的三角形彼此相等。
38. 在等底上且在相同二平行線之間的三角形彼此相等。
39. 在同底上且在底的同一側的相等三角形必在相同二平行線之間。
40. 等底且在底的同側的相等三角形也在相同二平行線之間。
41. 如果一個平行四邊形和一個三角形既同底又在二平行線之間,則平行四邊形是這個三角形的二倍。
42. 用已知直線角作平行 四邊形,使它等於已知三角形。
43. 在任何平行四邊形中,對角線兩邊的平行四邊形的補形彼此相等。
44. 用已知線段及已知直線角作一個平行四邊形,使它等於已知三角形。
45. 用一個已知直線角作一平行四邊形使它等於已知直線形。
46. 在已知線段上作一個正方形。
47. 在直角三角形中,直角所對的邊上的 正方形等於夾直角兩邊上正方形的和。
48. 如果在一個三角形中,一邊上的正方形等於這個三角形另外兩邊上正方形的和,則夾在後兩邊之間的角是直角。
邏輯聯結詞
 命題
命題 (1)或
1、用聯結詞“或”把p與q聯結起來稱為一個新命題,記作p∨q,讀作“p或q”。
2、命題p∨q的真假的判定:一真必真
p q p∨q
真 真 真
真 假 真
假 真 真
假 假 假
(2)且
1、用聯結詞“且”把p與q聯結起來稱為一個新命題,記作p∧q,讀作“p且q”。
2、命題p∧q的真假的判定:一假必假
p q p∧q
真 真 真
真 假 假
假 真 假
假 假 假
(3)非
1、對於一個命題p如果僅將它的結論否定,就得到一個新命題,記作┐p,讀作“非p”。
2、命題┐p的真假的判定:真假相對
p ┐p
真 假
假 真
《幾何原本》命題(特指)
特指歐幾里德的《幾何原本》中的被證明的命題,如下列48個命題:
1. 在一個已知有限直線上作一個等邊三角形。
2. 由一個已知點(作為端點)作一線段等於已知線段。
3. 已知兩條不相等的線段,試由大的上邊截取一條線段使它等於另外一條。
4. 如果兩個三角形有兩邊分別等於兩邊,而且這些相等的線段所夾的角相等,那么,它們的底邊等於底邊,三角形全等於三角形,而且其餘的角等於其餘的角,即那等邊所對的角。
5. 在等腰三角形中,兩底角彼此相等;並且,若向下延長兩腰,則在底以下的兩角也彼此相等。
6. 如果在一個三角形中,有兩角彼此相等,則等角所對的邊也彼此相等。
7. 在已知線段上(從它的兩個端點)作出相交於一點的二線段,則不可能在該線段(從它的兩個端點)的同側作出相交於另一點的另二條線段,使得作出的二線段分別等於前面二線段。即每個交點到相同端點的線段相等。
8. 如果兩個三角形的一個有兩邊分別等於另一個的兩邊,並且一個的底等於另一個的底,則夾在等邊中間的角也相等。
9. 二等分一個己知直線角。
10. 二等分已知有限直線。
11. 由已知直線上一已知點作一直線和已知直線成直角。
12. 由已知無限直線外一已知點作該直線的垂線。
13. 一條直線和另一條直線所交成的鄰角,或者是兩個直角或者它們等於兩個直角的和。
14. 如果過任意直線上點有兩條直線不在這一直線的同側,且和直線所成鄰角和等於二直角,則這兩條直線在同一直線上。
15. 如果兩直線相交,則它們交成的對頂角相等。
16. 在任意的三角形中,若延長一邊,則外角大於任何一個內對角。
17. 在任何三角形中,任何兩角之和小於兩直角。
18. 在任何三角形中,大邊對大角。
19. 在任何三角形中,大角對大邊。
20. 在任何三角形中,任意兩邊之和大於第三邊。
21. 如果由三角形的一條邊的兩個端點作相交於三角形內的兩條線段,由交點到兩端點的線段的和小於三角形其餘兩邊的和。但是,其夾角大於三角形的頂角。
22. 試由分別等於已知三條線段的三條線段作一個三角形:在這樣的三條已知線段中,任二條線段之和必須大於另外一條線段。
23. 在已知直線和它上面一點,作一個直線角等於己知直線角。
24. 如果兩個三角形中,一個的兩條邊分別與另一個的兩條邊相等,且一個的夾角大於另一個的夾角,則夾角大的所對的邊也較大。
25. 如果在兩個三角形中,一個的兩條邊分別等於另一個的兩條邊,則第三邊較大的所對的角也較大。
26. 如果在兩個三角形中,一個的兩個角分別等於另一個的兩個角,而且一邊等於另一個的一邊。即或者這邊是等角的夾邊,或者是等角的對邊。則它們的其他的邊也等於其他的邊,且其他的角也等於其他的角。
27. 如果一直線和兩直線相交所成的錯角彼此相等,則這二直線互相平行。
28. 如果一直線和二直線相交所成的同位角相等,或者同旁內角的和等於二直角,則二直線互相平行。
29. 一條直線與兩條平行直線相交,則所成的內錯角相等,同位角相等,且同旁內角的和等於二直角。
30. 一些直線平行於同一條直線,則它們也互相平行。
31. 過一已知點作一直線平行於已知直線。
32. 在任意三角形中,如果延長一邊,則外角等於二內對角的和,而且三角形的三個內角的和等於二直角。
33. 在同一方向(分別)連線相等且平行的線段(的端點),它們自身也相等且平行。
34. 在平行四邊形面片中,對邊相等,對角相等且對角線二等分其面片。
35. 在同底上且在相同兩平行線之間的平行四邊形彼此相等。
36. 在等底上且在相同二平行線之間的平行四邊形彼此相等。
37. 在同底上且在相同二平行線之間的三角形彼此相等。
38. 在等底上且在相同二平行線之間的三角形彼此相等。
39. 在同底上且在底的同一側的相等三角形必在相同二平行線之間。
40. 等底且在底的同側的相等三角形也在相同二平行線之間。
41. 如果一個平行四邊形和一個三角形既同底又在二平行線之間,則平行四邊形是這個三角形的二倍。
42. 用已知直線角作平行四邊形,使它等於已知三角形。
43. 在任何平行四邊形中,對角線兩邊的平行四邊形的補形彼此相等。
44. 用已知線段及已知直線角作一個平行四邊形,使它等於已知三角形。
45. 用一個已知直線角作一平行四邊形使它等於已知直線形。
46. 在已知線段上作一個正方形。
47. 在直角三角形中,直角所對的邊上的正方形等於夾直角兩邊上正方形的和。
48. 如果在一個三角形中,一邊上的正方形等於這個三角形另外兩邊上正方形的和,則夾在後兩邊之間的角是直角。
高考英語語法命題的若干規律
規律1 考查英語語法基礎知識
儘管高考英語的單項填空題的考點分布很廣,但可以肯定的是,它主要涉及的還是英語語法的基礎知識,只有具備一定的語法基礎,同時兼顧一定的解題方法和技巧,大部分考題都是可以做出來的。如:
1. Judy is going to marry the sailor she ______ in Rome last year. (2008重慶卷)
A. meets B. met C. has met D. would meet
【分析】B。根據句末的last year可知,空格處套用一般過去時。註:she met in Rome last year為修飾the sailor的定語從句。
2. Isn’t it amazing how the human body heals ______ after an injury? (2008江西卷)
A. himself B. him C. itself D. it
【分析】C。同學們在國中英語中就學過,當主語和賓語指同一個人或事物時,賓語必須要用反身代詞,不能用賓格代詞。註:heal oneself在此指“自愈”。
規律2 在語境中考查語法運用
近年來高考英語單項填空的一個最大特點就是突出語境考查,即將具體的語法知識置於特定的語境中進行考查,既考查運用語法知識的正確性,同時也考查運用語法知識的得體性。如:
1. I thought you’d be late for the concert, ______ we ended up getting there ahead of time. (2008湖南卷)
A. but B. or C. so D. for
【分析】A。比較空格前後兩句的意思:前面說“我原以為你聽音樂會會遲到的”,後面說“結果我們提前趕到了”。很顯然空格處應填一個錶轉折的連詞,這樣才符合句子的語境。
2. You ______ be hungry already—you had lunch only two hours ago! (2008浙江卷)
A. wouldn’t B. can’t C. mustn’t D. needn’t
【分析】B。做好此題要注意句子後半部的語境。既然you had lunch only two hours ago(你兩個小時前才吃過中飯),所以你現在“不可能”就餓了,所以答案選B。
規律3 綜合考查語法基礎知識
這裡說的綜合考查語法知識,指的是一道考題同時考查兩個或多個語法點,如將時態考點與語態考點綜合,將時態考點與主謂一致考點綜合,將非謂語動詞考點與並列句考點綜合,將複合句考點與簡單句考點綜合,等等。如:
1. —Did you go to the show last night?
—Yeah. Every boy and girl in the area ______ invited. (2008陝西卷)
A. were B. have been C. has been D. was
【分析】D。此題既考查時態的用法,同時又考查主語一致。根據問句中的時態和last night這一短語可知,此處談的是昨晚的事,故套用一般過去時,而不用現在完成時。另外,根據英語語法,當兩個或多個名詞並列作主語,且受到every的修飾時,其後謂語動詞要用單數。故答案選D。
2. —Do you have any problems if you ______ this job?
—Well, I’m thinking about the salary... (2008湖南卷)
A. offer B. will offer C. are offered D. will be offered
【分析】C。此題既考查時態,同時又考查被動語態。由於if引導的是條件狀語從句,所以要用一般現在時表示將來意義,而不能直接使用將來時態,故可排除B和D;再根據offer sb sth(為某人提供某物)這一句式可知,sb與offer之間為被動關係,故要用被動語態。
規律4 在特定語境中考查邊緣知識
這裡所說的邊緣知識,指的是一般語法上涉及得較少,許多同學在複習中接觸較少的知識點。這類考點有的雖然一般語法書講得較少,但並不意味著它在英語中並不重要。如:
1. When she first arrived in China, she wondered what the future might have ______ for her, but now all her worries are gone. (2008湖北卷)
A. in need B. in time C. in preparation D. in store
【分析】D。in store for是習語,其意為“為……儲備著”“等待著……”,如:The runner kept some energy in store for spurting at the end. 那名賽跑的人為最後的衝刺貯存精力。There’s a surprise in store for you. 你一定會大吃一驚的。
2. Elizabeth has already achieved success ______ her wildest dreams. (2008陝西卷)
A. at B. beyond C. within D. upon
【分析】B。beyond one’s wildest dreams為習語,其意為“遠遠超出想像或希望”,這可能是許多同學不太熟悉的一個用法,並且它在教材中也沒有出現過。又如:The scheme succeeded beyond my wildest dreams. 這個計畫超乎異常地成功了。
3. Engines are to machines _______ hearts are to animals. (2006山東卷)
A. as B. that C. what D. which
【分析】C。這是一個比較難的考題,就算是放到大學四、六級考試中也絕對算是難題,一般的英語語法書也絕對沒有涉及此問題,就是連最新出版的《牛津高階英漢雙解詞典》和《朗文當代高級英語辭典》的what詞條下也找不到此用法。現分析如:what 在此用作連詞,其意為“好比”“猶如”“就像”,用以引導相似狀語從句。如:Air is to us what water is to fish. 我們離不開空氣,就像魚兒離不開水一樣。Reading is to the mind what food is to the body. 讀書與思想的關係就好比食物與健康的關係。
規律5 在複雜語境中考查簡單知識
有的知識點本來很簡單,如果是單獨進行考查,一般學生都不會出錯,但是如果將其置於一個較複雜的語境中,許多考生就可能受複雜句子結構的影響而選錯。如:
1. —Could you tell me how to get to Victoria Street? (2008遼寧卷)
—Victoria Street? ______ is where the Grand Theatre is.(www.yygrammar.com)
A. Such B. There C. That D. This
【分析】C。此題考查指示代詞that的遠指用法,這是同學們在國中就學過的知識了。但是,由於命題者將這個本來很簡單的知識點放到了一個比較複雜的對話背景中,分散了同學們對被考查知識點的注意力,所以許多同學在做此題時選錯了答案。請再看一個類似的例子:That day we visited an old house. That’s where he spent his last years. 那天我們去參觀了一座老房子,那就是他去世前幾年他住的地方。這類句式如果改用this,則表近指,如:This is where the river is deepest. 這是河流的最深處。This is where we change from car to bus. 這就是我們從小汽車換乘公共汽車的地方。
2. If the weather had been better, we could have had a picnic. But it ______ all day. (2008全國Ⅱ)
A. rained B. rains C. has rained D. is raining
【分析】A。此題考查一般過去時的用法,但試題使用了虛擬語氣作為命題背景,且該虛擬語氣談的是過去情況(根據句中的had been和could have had可知),句意為“要是(當時)天氣好一點,我們就可以去野餐了”。該虛擬語氣的言外之意是“(由於天氣不好)我們沒有去野餐”。為什麼沒去呢?but後說的就是其原因:整天都在下雨。這裡說的“下雨”,顯然指的是過去的情況,故用一般過去時。
規律6 利用思維定勢設定干擾項
同學們在對某個知識點或重要句式進行反覆操練後,往往會形成一定的思維定勢。由於思維定勢在很大程度上帶有慣性,有時甚至是惰性,所以同學們在做題時若不仔細讀題,認真分析,很可能會受此影響,步入誤區。如:
1. Nancy enjoyed herself so much ______ she visited her friends in Sydney last year. (2008福建卷)
A. that B. which C. when D. where
【分析】C。本題很容易讓考生受思維定勢的負面影響,見到so馬上選擇that,殊不知此題考查的是when引導的時間狀語從句,句意為:南希去年拜訪悉尼的朋友時過得非常開心。如果選A,則句意為:南希玩得如此開心以至於拜訪了悉尼的幾個朋友。顯然,意思不合邏輯。
2. —Have you known Dr. Jackson for a long time?
—Yes, since she ______ the Chinese Society. (2008寧夏卷)
A. has joined B. joins C. had joined D. joined
【分析】D。許多同學認為since總是要與現在完成時連用的,所以誤選了A。其實,本句中since she join the Chinese Society為I have known Dr. Jackson since she joined the Chinese Society之省略。連詞since所搭配的時態通常是:主句用現在完成時,從句用一般過去時。
3. —They are quiet, aren’t they?
—Yes. They are accustomed ______ at meals. (2008江蘇卷)
A. to talk B. to not talk C. to talking D. to not talking
【分析】D。此題設計得很巧妙。有的同學在排除選項B時,同時也會排除選項D,因為它們的結構太相似了。但事實上,正確答案正是D。be accustomed to的意思是“習慣於做……”,其中的to通常被認為是介詞,後接名詞或動名詞,但在現代英語中,其後也可接動詞原形,即其中的to被視為不定式符號。照此分析,好像四個答案都可以,但其實只有D最佳。因為根據語境分析(注意其中的are quiet, yes等關鍵詞),此題應選一個否定式,故可排除A和C。另外,從語法上分析,非謂語動詞的否定式總是將not置於非謂語動詞之前,所以C應改為not to talk才對;至於D,由於其中的to是介詞,其後接動名詞talking作賓語,動名詞talking的否定式為not talking,所以說to not talking是正確的。
規律7 直接引用詞典原句進行命題
近年來,高考英語命題一直有個習慣,就是喜歡從一些原版英語詞典上直接引用例句進行命題。這點希望引起同學們的注意。下面請看幾個例子:
1. My neighbor asked me to go for ______ walk, but I don’t think I’ve got ______ energy. (2008遼寧卷)
A. a; 不填 B. the; the C. 不填; the D. a; the
【分析】D。go for a walk為固定表達,意為“去散步”;have got the energy意為“有精力”。此題出自Cambridge Advanced Learner’s Dictionary的the詞條,詞典上的原句為:I’d like to go out this evening, but I don’t think I’ve got the energy.
2. —I’d like some more cheese.
—Sorry, there’s ______ left. (2008浙江卷)
A. some B. none C. a little D. few
【分析】B。由於cheese不可數,故可排除D;再根據句中的sorry可知,此處應填表否定意義的none。註:此題出自Cambridge Advanced Learner’s Dictionary的none詞條,詞典上的原句為:“I’d like some more cheese.” “I’m sorry there’s none left.”
3. He found it increasingly difficult to read, ______ his eyesight was beginning to fail. (2008山東卷)
A. though B. for C. but D. so
【分析】B。for在此表原因。又如:He shook his head, for he thought differently. 他搖了搖頭,因為他有不同想法。 註:此題出自Longman Dictionary of Contemporary English的for詞條,詞典上的原句為:He found it increasingly difficult to read, for his eyesight was beginning to fail.
形式分析
 命題
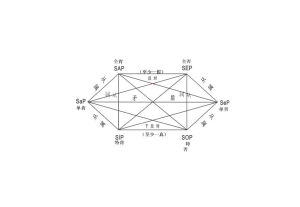
命題 對命題形式的進一步分析,要深入到最簡單命題內部的非命題 成分。在現代邏輯中,類似"蘇格拉底是人"這樣的命題,被認為是最簡單的命題。若以s代表"蘇格拉底",以M代表"人",該類命題就可記為M(s),這表示某一個體s具有性質R。推廣來說,最簡單的命題的形式為F(x),可讀作論域中的個體x具有性質F;較為複雜的形式可以有填G(x,y)),可讀作論域中的 個體x,y)之間具有關係G。在這裡,x,y),...稱為個體變項;F,G,...稱為謂詞變項,而F是一元的,G是二元的。n個個體變項之間有n元關係H就記為H(x,...,xn-1)。若以L代表"處在流動的狀態",而"每個事物都處在流動的狀態"就可記為風xL(x),這可讀為:對論域裡所有個體x 而言,x 處在流動的狀態。其中,風x 叫做全稱量詞,風是全稱量詞符號。若以B代表"尚未被人認識的",則"至少有一個東西是尚未被人認識的",可記為 ヨxB(x),讀作論域中至少有一個體 x,x 尚未被人認識。在這裡ヨx 是存在量詞,而ヨ是存在量詞符號。"不存在一個最大的實數", 可表示為 填ヨy)風x(y)>x),其論域為實數。"任意兩實數之間至少有一個實數",可表示為風x風y)ヨz(x 邏輯理論。

