簡介
命題永真公式亦稱重言式，是一種命題公式。對於任何指派，其真值總是真的命題公式稱為命題的永真公式。
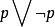命題永真公式
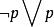命題永真公式
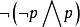命題永真公式例如是一個永真公式，因為無論給力以什麼樣的真值其總有真值T，永真公式反映了命題的邏輯規律.例如永真公式反映了排中律， 反映了矛盾律等。永真公式是命題邏輯的研究重點，在一個融貫的命題演算公理系統中推演出的公式都是永真公式。
意義
永真公式所表示的直覺意義與人們通常的直覺思維不盡相符，因此被視為“怪論”，稱這類命題演算中的永真公式為蘊涵怪論。
如公式 p→(q→p) 是一蘊涵怪論，它是永真公式，而它反映的邏輯規律“如果 p，則 q 蘊涵 p "，不符合人們日常的思維方式。對於蘊涵怪論的態度有多種，有人認為它既然是永真公式，就應將它與其他永真公式一樣對待，甚至有人將一些蘊涵怪論，如 p→(q→p) 作為公理。有人則不承認蘊涵怪論，設法在命題演算系統中避免它們的出現。有的認為蘊涵怪論也是永真公式，只要將它們與其他永真公式區別開就可以了，中國數理邏輯學家莫紹撰在20世紀 50年代初建立的一個命題演算系統就能很好地區別蘊涵怪論和其他永真公式。
命題演算的運算律
反映命題演算規律永真的等價式稱為命題演算的運算律。
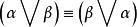命題永真公式例如，設 α,β 為命題， 反映了真值聯結詞“V”運算的交換律。主要的命題演算的運算律有交換律，結合律，分配律，德·摩根律等。
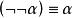命題永真公式命題演算的運算律與命題演算的系統有關，不同的系統可有不同的運算律。例如，雙否律在古典系統中成立，但在直覺主義系統中就不成立。正確地使用運算律能使公式得以簡化並更深刻地揭示這些公式反映的邏輯規律。
