基本概念
在命題邏輯中,命題又有命題常元和命題變元之分,一個確定的具體的命題,稱為 命題常元;一個不確定的泛指的任意命題,稱為命題變元,顯然,命題變元不是命題,只有用一個特定的命題,即對該命題變元賦值0或1才能確定它的真值。
命題常元和命題變元都用字母p,q,r,…表示,在命題邏輯中我們只關心命題的真值,故給出如下形式的定義。
定義1 以真或1、假或0為其變域的變元,稱為命題變元;真或1、假或0稱為命題常元。
命題常元、變元及聯結詞是形式描述命題及其推理的基本語言成分,用它們可以形式地描述更為複雜的命題 。
相關概念及結論
定義2 單個命題變元和命題常元稱為原子命題公式,簡稱原子公式 。
定義3 合式公式是由下列規則生成的公式:
①單個原子公式是合式公式。
②若A是一個合式公式,則¬A也是一個合式公式。
③若A、B是合式公式,則A∧B、A∨B、A→B和A↔B都是合式公式。
④只有有限次使用①、②和③生成的公式才是合式公式。
合式公式也稱為命題公式或命題形式,簡稱為公式。
按照上述定義,下面的符號串是公式:
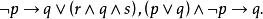 命題常元
命題常元下面的符號串不是公式:
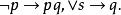 命題常元
命題常元定義3 如果B是公式A中的一部分,且B為公式,則稱B是公式A的子公式。
當合式公式比較複雜時,常常使用很多例括弧,為了減少圓括弧的使用量,可作以下約定:
①規定聯結詞的優先權由高到低的次序為:¬、∧、∨、→、↔。
②相同的聯結詞按從左至右次序計算時,圓括弧可省略。
③最外層的圓括弧可以省略。
對公式中的命題變元各指定一個真值,稱為對公式的賦值或解釋,若指定的一組值是公式真值為1,稱這組值為公式的成真賦值;若指定的一組值是公式真值為0,稱這組值為公式的成假賦值。
定義4 對於公式中命題變元的每一種可能的賦值,以及由它們確定出的公式真值所列成的表,稱為該公式的真值表。
用歸納法不難證明,對於含有n個命題變元的公式,有2 個賦值,即在該公式的真值表中有2 行。
為方便構造真值表,特約定如下:
①將n個命題變元按字母序或下標序排列,列出2 個賦值,賦值從00…0開始,然後按二進制加法依次寫出每個賦值,直到11…1為止。
②若公式較複雜,可先列出各子公式的真值(若有括弧,則應從裡層向外層展開)。
③最後列出所求公式的真值 。

