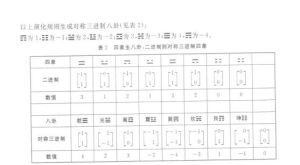
定義
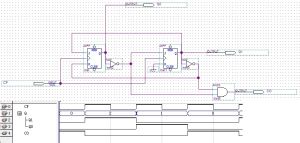二進碼三進制的同步減法計數器對稱三進制能比二進制更方便的表示所有整數。
三進制是“逢三進一，退一還三”的進制。
三進制數碼包括“0，1和2。”電信號（—1）、0、1。
三進制數位小數點前從右往左依次是1位，3位，9位，27位，81位，243位……
三進制數位小數點後從左往右依次是3分位，9分位，27分位，81分位……
寫時注意應打括弧，加下標的3，如（1201）3。讀作一二零一，不能讀成一千二百零一，這是因為它們對應於27位，9位，3位和1位，不是千百十個位！
一些常見的十進制數換三進制表：
| 十進制 | 三進制 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 10 |
| 4 | 11 |
| 5 | 12 |
| 6 | 20 |
| 7 | 21 |
| 8 | 22 |
| 9 | 100 |
| 10 | 101 |
| ... | ... |
舉例
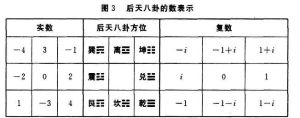對稱三進制允許在天平兩端放置砝碼，問N個砝碼如何才能稱出最多的整克物體？
答案：1.一個砝碼取1克，只能稱1克。
2.二個砝碼取1克，3克
右盤3，左盤1。稱2克
右盤3。稱3克
右盤1，3。稱4克
3.三個砝碼取1克，3克，9克
右盤9，左盤1，3。稱5克
右盤9，左盤3。稱6克
右盤9，1，左盤3。稱7克
右盤9，左盤1。稱8克
右盤9。稱9克
右盤9，1。稱10克
右盤9，3，左盤1。稱11克
右盤9，3。稱12克
右盤9，3，1。稱13克
4.四個砝碼取1克，3克，9克，27克。
............
其中的1，3，9，27，81等都是三進制數的數位。
表示形式
三進制一般有兩種表示形式：
一種是以0，1，2為基本字元的表示形式。例如，365在這種表示形式中的寫法是111112。
一種是以-1，0，1為基本字元的表現形式。例如，365在這種表示形式中的寫法是1FFFFFF(我們用F表示-1)。這種表示法也被稱作對稱三進制或平衡三進制。
特點
三進制是“逢三進一,退一還三”的進制。
三進制數碼包括“0，1和2。”電信號（—1）、0、1。
三進制數位小數點前從右往左依次是1位，3位，9位，27位，81位，243位……
三進制數位小數點後從左往右依次是3分位，9分位，27分位，81分位……
寫時注意應打括弧，加下標的3，如（1201）3。讀作一二零一，不能讀成一千二百零一，這是因為它們對應於27位，9位，3位和1位，不是千百十個位
運算規則
普通三進制的四則運算
加法：0+0=0，0+1=1，0+2=2，1+0=1，1+1=2，1+2=10，2+0=2，2+1=10，2+2=11
減法：0－0=0，1－0=1，2-1=1，1－1=0，2－1=1，10-1=2，2-2=0，10-2=1，11-2=2
乘法：0×0=0，0×1=0，0×2=0，1×0=0，1×1=1，1×2=2，2×0=0，2×1=2，2×2=11
除法：0÷1=0，1÷1=1，2÷1=2，1÷2=0.1111...
對稱三進制的四則運算
加法：F+F=F1，F+0=F，F+1=0，0+F=F，0+0=0，0+1=1，1+F=0，1+0=1，1+1=1F
減法：F－F=0，F－0=F，F-1=F1，0－F=1，0－0=0，0-1=F，1-F=1F，1-0=1，1-1=0
乘法：F×F=1，F×0=0，F×1=F，0×F=0，0×0=0，0×1=0，1×F=F，1×0=0，1×1=1
除法：F÷F=1，F÷1=F，0÷F=0，0÷1=1,1÷F=F，1÷1=1
對稱三進制的邏輯運算
或：F∨F=F，F∨0=0，F∨1=1，0∨F=0，0∨0=0，0∨1=1，1∨F=1，1∨0=1，1∨1=1
與：F∧F=F，F∧0=F，F∧1=F，0∧F=F，0∧0=0，0∧1=0，1∧F=F，1∧0=0，1∧1=1
非：¬F=1，¬0=0，¬1=F
與十進制和二進制的比較
整數的三進制表示法不如二進制那樣冗長，但仍然比十進制要長。例如，365在二進制中的寫法是101101101（9個數字），在三進制中的寫法是111112（6個數字）。
| 1到27 | |||||||||
| 三進制 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| 對稱三進制 | 1 | 1F | 10 | 11 | 1FF | 1F0 | 1F1 | 10F | 100 |
| 二進制 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 |
| 十進制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 三進制 | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 | 200 |
| 對稱三進制 | 101 | 11F | 110 | 111 | 1FFF | 1FF0 | 1FF1 | 1F0F | 1F00 |
| 二進制 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 |
| 十進制 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 三進制 | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 | 1000 |
| 對稱三進制 | 1F01 | 1F1F | 1F10 | 1F11 | 10FF | 10F0 | 10F1 | 100F | 1000 |
| 二進制 | 10011 | 10100 | 10101 | 10110 | 10111 | 11000 | 11001 | 11010 | 11011 |
| 十進制 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 3的冪 | |||||
| 三進制 | 1 | 10 | 100 | 1000 | 10000 |
| 對稱三進制 | 1 | 10 | 100 | 1000 | 10000 |
| 二進制 | 1 | 11 | 1001 | 11011 | 1010001 |
| 十進制 | 1 | 3 | 9 | 27 | 81 |
| 冪 | 3（0） | 3（1） | 3（2） | 3（3） | 3（4） |
| 三進制 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 |
| 對稱三進制 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 |
| 二進制 | 1111 0011 | 10 1101 1001 | 1000 1000 1011 | 1 1001 1010 0001 | 100 1100 1110 0011 |
| 十進制 | 243 | 729 | 2 187 | 6 561 | 19 683 |
| 冪 | 3（5） | 3（6） | 3（7） | 3（8） | 3（9） |
| 小數 | ||||||
| 三進制 | 0.111111111111... | 0.1 | 0.020202020202... | 0.012101210121... | 0.011111111111... | 0.010212010212... |
| 對稱三進制 | 0.111111111111... | 0.1 | 0.1F1F1F1F1F... | 0.1FF11FF11FF1... | 0.011111111111... | 0.0110FF0110FF... |
| 二進制 | 0.1 | 0.010101010101... | 0.01 | 0.001100110011... | 0.00101010101... | 0.001001001001... |
| 十進制 | 0.5 | 0.333333333333... | 0.25 | 0.2 | 0.166666666666... | 0.142857142857... |
| 分數 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 |
| 三進制 | 0.010101010101... | 0.01 | 0.002200220022... | 0.002110021100... | 0.002020202020... | 0.002002002002... |
| 對稱三進制 | 0.010101010101... | 0.01 | 0.010F010F010F... | 0.01F1101F1100... | 0.01F1F1F1F0... | 0.01F01F01F01F... |
| 二進制 | 0.001 | 0.000111000111... | 0.000110011001... | 0.000101110100... | 0.000101010101... | 0.000100111011... |
| 十進制 | 0.125 | 0.111111111111... | 0.1 | 0.090909090909... | 0.083333333333... | 0.076923076923... |
| 分數 | 1/8 | 1/9 | 1/10 | 1/11 | 1/12 | 1/13 |
比較
1.對稱三進制採用-1，0，1作為基本字元，而普通三進制採用0，1，2作為基本字元。
2.對稱三進制不需要符號位就能表示負數，而普通三進制需要符號位才能表示負數。
3.對稱三進制乘法比較簡單，移位、取非、相加就可以完成，便於處理；普通三進制，處理起來比較麻煩。
4.對稱三進制在表示自然數的時候，比普通二進制要長。
5.對稱三進制在表示0.5〈10〉~1〈10〉之間的數的時候，整數部分為1，不直觀；普通三進制沒有這種現象。
轉換
整數部分，一般使用長除法，用基數除待轉換數或上一步的商，求得餘數或補數，直至最後的商為零。將各次餘數從後往前排列，即為目標進制下的整數部分。小數部分，一般使用長乘法，用基數乘待轉換數或上一步的積，求得整數部分，將證書部分從前往後排列，即為目標進制下的小數部分正負數需要分別處理。
十進制到普通三進制
例如，2356
2356/3=785餘1，785/3=261餘2，261/3=87，87/3=29，29/3=9餘2，9/3=3，3/3=1，1/3=0餘1
以上得知，2356的三進制為10020021
十進制到對稱三進制
例如，2356，2356/3=785餘1；785/3=262少1，262/3=87餘1，87/3=29，29/3=10少1，10/3=3餘1，3/3=1，1/3=0餘1
以上得知，2356的對稱三進制為101F01F1
二進制到對稱三進制
正數
比如0111 1010(十進制122)
01111010/11=101001少1;101001/11=1110少1;1110/11=101少1;101/11=10少1;10/11=1少1;1/11=0餘1
01111010的對稱3進制為1FFFFF
負數
比如1011 1010(-70)
取原碼-1000110
1000110/11=10111餘1;10111/11=1000少1;1000/11=11少1;11/11=1;1/11=0餘1
得10FF1，逐位取非，得對稱三進制為F011F
三進制計算機
現今的計算機都使用“二進制”數字系統，儘管它的計算規則非常簡單，但其實“二進制”邏輯並不能完美地表達人類的真實想法。相比之下，“三進制”邏輯更接近人類大腦的思維方式。因為在一般情況下，我們對問題的看法不是只有“真”和“假”兩種答案，還有一種“不知道”。在三進制邏輯學中，符號“1”代表“真”；符號“-1”代表“假”；符號“0”代表“不知道”。顯然，這種邏輯表達方式更符合計算機在人工智慧方面的發展趨勢。它為計算機的模糊運算和自主學習提供了可能。只可惜，目前電子工程師對這種非二進制的研究大都停留在表面或形式上，沒有真正深入到實際套用中去。
不過，凡事都有一個例外，三進制計算機並非沒有在人類計算機發展史上出現過。其實，早在上世紀50、60年代。一批莫斯科國立大學的研究員就設計了人類歷史上第一批三進制計算機“Сетунь”和“Сетунь 70”（“Сетунь”是莫大附近一條流入莫斯科河的小河的名字）。
“Сетунь”小型數字計算機的設計計畫由科學院院士С·Л·Соболев在1956年發起。這個計畫的目的是為大專院校、科研院所、設計單位和生產車間提供一種價廉物美的計算機。為此，他在莫大計算機中心成立了一個研究小組。該小組最初由9位年輕人（4名副博士、5名學士）組成，都是工程師和程式設計師。С·Л·Соболев、К·А·Семендяев、М·Р·Шура-Бура和И·С·Березин是這個小組的永久成員。他們經常在一起討論計算機架構的最最佳化問題以及如何依靠現有的技術去實現它。他們甚至還構想了一些未來計算機的發展思路。
隨著技術的進步，真空管和電晶體等傳統的計算機元器件逐漸被淘汰，取而代之的是速度更快、可靠性更好的鐵氧體磁芯和半導體二極體。這些電子元器件組成了一個很好的可控電流變壓器，這為三進制邏輯電路的實現提供了可能，因為電壓存在著三種狀態：正電壓（“1”）、零電壓（“0”）和負電壓（“-1”）。三進制邏輯電路非但比二進制邏輯電路速度更快、可靠性更高，而且需要的設備和電能也更少。這些原因促成了三進制計算機“Сетунь”的誕生。
“Сетунь”是一台帶有快速乘法器的時序計算機。小型的鐵氧體隨機存儲器（容量為3頁，即54字）充當快取，在主磁鼓存儲器中交換頁面。這台計算機支持24條指令，其中3條為預留指令，目前不用。
三進制代碼的一個特點是對稱，即相反數的一致性，因此它就和二進制代碼不同，不存在“無符號數”的概念。這樣，三進制計算機的架構也要簡單、穩定、經濟得多。其指令系統也更便於閱讀，而且非常高效。
在這群天才青年日以繼夜的開發和研製下，“Сетунь”的樣機於1958年12月準備完畢。在頭兩年測試期，“Сетунь”幾乎不需要任何調試就運行得非常順利，它甚至能執行一些現有的程式。1960年，“Сетунь”開始公共測試。
1960年4月，“Сетунь”就順利地通過了公測。它在不同的室溫下都表現出驚人的可靠性和穩定性。它的生產和維護也比同期其它計算機要容易得多，而且套用面廣，因此“Сетунь”被建議立即投入批量生產。
不幸的是，蘇聯官僚對這個不屬於經濟計畫一部分的“科幻產物”持否定的態度。他們甚至勒令其停產。而此時，對“Сетунь”的訂單卻如雪片般從各方飛來，包括來自國外的訂單，但10到15台的年產量遠不足以應付市場需求，更不用說出口了。很快，計畫合作生產“Сетунь”的捷克斯洛伐克工廠倒閉了。1965年，“Сетунь”停產了。取而代之的是一種二進制計算機，但價格卻貴出2.5倍。
“Сетунь”總共生產了50台（包括樣機）。30台被安裝在高等院校，其餘的則在科研院所和生產車間落戶。從加里寧格勒到雅庫茨克，從阿什哈巴德到新西伯利亞，全蘇都能看到“Сетунь”的身影。各地都對“Сетунь”的反應不錯，認為它編程簡單（不需要使用彙編語言），支持反向波蘭表示法，適用於工程計算、工業控制、計算機教學等各個領域。
有了“Сетунь”的成功經驗，研究員們決定不放棄三進制計算機的計畫。他們在1970年推出了“Сетунь 70”型計算機。“Сетунь 70”對三進制的特性和概念有了進一步的完善和理解：建立了三進制位元組——“tryte”（對應於二進制的“byte”），每個三進制位元組由6個三進制位（“trit”，約等於9.5個二進制位“bit”）構成；指令集符合三進制邏輯；算術指令允許更多的運算元長——1、2和3位元組（三進制），結果長度也擴展到6位元組（三進制）。
對“Сетунь 70”而言，傳統計算機的“字”的概念已經不存在了。編程的過程就是對三進制運算和三進制地址的操作。這些基於三進制位元組的命令將會通過對虛擬指令的編譯而得到。當然，程式設計師們不必考慮這些——他們只需直接和運算元及參數打交道即可。
“Сетунь 70”是一台雙堆疊計算機。其回叫堆疊用來調用子程式。這一簡單的改進啟發了荷蘭計算機科學家艾茲格·W·迪科斯徹，為他日後提出“結構化程式設計”思想打下了基礎。
“Сетунь 70”成了莫斯科國立大學三進制計算機的絕唱。由於得不到上級的支持，這個科研項目不得不無限期停頓下來。
套用歷史
現今的計算機都使用“二進制”數字系統，儘管它的計算規則非常簡單，但其實“二進制”邏輯並不能完美地表達人類的真實想法。相比之下，“三進制”邏輯更接近人類大腦的思維方式。因為在一般情況下，我們對問題的看法不是只有“真”和“假”兩種答案，還有一種“不知道”。在三進制邏輯學中，符號“1”代表“真”；符號“-1”代表“假”；符號“0”代表“不知道”。顯然，這種邏輯表達方式更符合計算機在人工智慧方面的發展趨勢。它為計算機的模糊運算和自主學習提供了可能。只可惜，電子工程師對這種非二進制的研究大都停留在表面或形式上，沒有真正深入到實際套用中去。
不過，凡事都有一個例外，三進制計算機並非沒有在人類計算機發展史上出現過。其實，早在上世紀50、60年代。一批莫斯科國立大學的研究員就設計了人類歷史上第一批三進制計算機“Сетунь”和“Сетунь70”（“Сетунь”是莫大附近一條流入莫斯科河的小河的名字）。
“Сетунь”小型數字計算機的設計計畫由科學院院士С·Л·Соболев在1956年發起。這個計畫的目的是為大專院校、科研院所、設計單位和生產車間提供一種價廉物美的計算機。為此，他在莫大計算機中心成立了一個研究小組。該小組最初由9位年輕人（4名副博士、5名學士）組成，都是工程師和程式設計師。С·Л·Соболев、К·А·Семендяев、М·Р·Шура-Бура和И·С·Березин是這個小組的永久成員。他們經常在一起討論計算機架構的最最佳化問題以及如何依靠現有的技術去實現它。他們甚至還構想了一些未來計算機的發展思路。
隨著技術的進步，真空管和電晶體等傳統的計算機元器件逐漸被淘汰，取而代之的是速度更快、可靠性更好的鐵氧體磁芯和半導體二極體。這些電子元器件組成了一個很好的可控電流變壓器，這為三進制邏輯電路的實現提供了可能，因為電壓存在著三種狀態：正電壓（“1”）、零電壓（“0”）和負電壓（“-1”）。三進制邏輯電路非但比二進制邏輯電路速度更快、可靠性更高，而且需要的設備和電能也更少。這些原因促成了三進制計算機“Сетунь”的誕生。
“Сетунь”是一台帶有快速乘法器的時序計算機。小型的鐵氧體隨機存儲器（容量為3頁，即54字）充當快取，在主磁鼓存儲器中交換頁面。這台計算機支持24條指令，其中3條為預留指令，不用。
三進制代碼的一個特點是對稱，即相反數的一致性，因此它就和二進制代碼不同，不存在“無符號數”的概念。這樣，三進制計算機的架構也要簡單、穩定、經濟得多。其指令系統也更便於閱讀，而且非常高效。
在這群天才青年日以繼夜的開發和研製下，“Сетунь”的樣機於1958年12月準備完畢。在頭兩年測試期，“Сетунь”幾乎不需要任何調試就運行得非常順利，它甚至能執行一些現有的程式。1960年，“Сетунь”開始公共測試。
1960年4月，“Сетунь”就順利地通過了公測。它在不同的室溫下都表現出驚人的可靠性和穩定性。它的生產和維護也比同期其它計算機要容易得多，而且套用面廣，因此“Сетунь”被建議立即投入批量生產。
不幸的是，蘇聯官僚對這個不屬於經濟計畫一部分的“科幻產物”持否定的態度。他們甚至勒令其停產。而此時，對“Сетунь”的訂單卻如雪片般從各方飛來，包括來自國外的訂單，但10到15台的年產量遠不足以應付市場需求，更不用說出口了。很快，計畫合作生產“Сетунь”的捷克斯洛伐克工廠倒閉了。1965年，“Сетунь”停產了。取而代之的是一種二進制計算機，但價格卻貴出2.5倍。
“Сетунь”總共生產了50台（包括樣機）。30台被安裝在高等院校，其餘的則在科研院所和生產車間落戶。從加里寧格勒到雅庫茨克，從阿什哈巴德到新西伯利亞，全蘇都能看到“Сетунь”的身影。各地都對“Сетунь”的反應不錯，認為它編程簡單（不需要使用彙編語言），支持反向波蘭表示法，適用於工程計算、工業控制、計算機教學等各個領域。
有了“Сетунь”的成功經驗，研究員們決定不放棄三進制計算機的計畫。他們在1970年推出了“Сетунь70”型計算機。“Сетунь70”對三進制的特性和概念有了進一步的完善和理解：建立了三進制位元組——“tryte”（對應於二進制的“byte”），每個三進制位元組由6個三進制位（“trit”，約等於9.5個二進制位“bit”）構成；指令集符合三進制邏輯；算術指令允許更多的運算元長——1、2和3位元組（三進制），結果長度也擴展到6位元組（三進制）。
對“Сетунь70”而言，傳統計算機的“字”的概念已經不存在了。編程的過程就是對三進制運算和三進制地址的操作。這些基於三進制位元組的命令將會通過對虛擬指令的編譯而得到。當然，程式設計師們不必考慮這些——他們只需直接和運算元及參數打交道即可。
“Сетунь70”是一台雙堆疊計算機。其回叫堆疊用來調用子程式。這一簡單的改進啟發了荷蘭計算機科學家艾茲格·W·迪科斯徹，為他日後提出“結構化程式設計”思想打下了基礎。
“Сетунь70”成了莫斯科國立大學三進制計算機的絕唱。由於得不到上級的支持，這個科研項目不得不無限期停頓下來。
