十六進制的表示方法
十六進制照樣採用位置計數法,位權是16為底的冪。對於n位整數,m位小數的十六進制數用加權係數的形式表示如下:
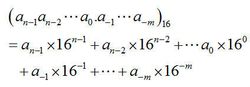 十六進制
十六進制舉例說明
16進制的20表示成10進制就是:2×16¹+0×16º=32
10進制的32表示成16進制就是:20
十進制數可以轉換成十六進制數的方法是:十進制數的整數部分“除以16取余”,十進制數的小數部分“乘16取整”,進行轉換。
比如說十進制的0.1轉換成八進制為0.0631463146314631。就是0.1乘以8=0.8,不足1不取整,0.8乘以8=6.4,取整數6, 0.4乘以8=3.2,取整數3,依次下算。
編程中,我們常用的還是10進制.畢竟C/C++是高級語言。
比如:
int a = 100,b = 99;
不過,由於數據在計算機中的表示,最終以二進制的形式存在,所以有時候使用二進制,可以更直觀地解決問題。但二進制數太長了。比如int 類型占用4個位元組,32位。比如100,用int類型的二進制數表達將是:
| 0000 | 0000 | 0000 | 0000 | 0110 | 0100 |
面對這么長的數進行思考或操作,沒有人會喜歡。因此,C,C++ 沒有提供在代碼直接寫二進制數的方法。用16進制或8進制可以解決這個問題。因為,進制越大,數的表達長度也就越短。不過,為什麼偏偏是16或8進制,而不其它的,諸如9或20進制呢?2、8、16,分別是2的1次方、3次方、4次方。這一點使得三種進制之間可以非常直接地互相轉換。8進制或16進制縮短了二進制數,但保持了二進制數的表達特點。在下面的關於進制轉換的課程中,你可以發現這一點。
轉換
二進制轉換十進制
二進制數第0位的權值是2的0次方,第1位的權值是2的1次方……
所以,設有一個二進制數:101100100,轉換為10進制為:356
用橫式計算
0×2+0×2+1×2+0×2+0×2+1×2+1×2+0×2+1×2=356
0乘以多少都是0,所以我們也可以直接跳過值為0的位:
1×2+1×2+1×2+1×2=356
4+32+64+256 =356
八進制轉換十進制
八進制就是逢8進1。
八進制數採用 0~7這八數來表達一個數。
八進制數第0位的權值為8的0次方,第1位權值為8的1次方,第2位權值為8的2次方……
所以,設有一個八進制數:1507,轉換為十進制為:839,具體方法如下:
可以用橫式直接計算:
7×8+0×8+5×8+1×8=839
也可以用豎式表示
第0位 7×8=7
第1位 0×8=0
第2位 5×8=320
第3位 1×8=512
十六進制轉換十進制
16進制就是逢16進1,但我們只有0~9這十個數字,所以我們用A,B,C,D,E,F這六個字母來分別表示10,11,12,13,14,15。字母不區分大小寫。
十六進制數的第0位的權值為16的0次方,第1位的權值為16的1次方,第2位的權值為16的2次方……
所以,在第N(N從0開始)位上,如果是數β (β大於等於0,並且β小於等於 15,即:F)表示的大小為 β×16的N次方。
假設有一個十六進數 2AF5
直接計算就是:
5×16+F×16+A×16+2×16=10997
也可以用豎式表示:
第0位: 5×16=5
第1位: F×16^1=240
第2位: A×16=2560
第3位: 2×16=8192
-------------------------------
10997
此處可以看出,所有進制換算成10進制,關鍵在於各自的權值不同。
假設有人問你,十進數1234 為什麼是一千二百三十四?你盡可以給他這么一個算式:
1234 = 1×10+2×10+3×10+4×10
十六進制互相轉換
首先我們來看一個二進制數:1111,它是多少呢?
你可能還要這樣計算:1×2+1×2+1×2+1×2=1×1+1×2+1×4+1×8=15。
然而,由於1111才4位,所以我們必須直接記住它每一位的權值,並且是從高位往低位記,:8、4、2、1。即,最高位的權值為2=8,然後依次是 2=4,2=2,2=1。
記住8421,對於任意一個4位的二進制數,我們都可以很快算出它對應的10進制值。
下面列出四位二進制數 xxxx 所有可能的值(中間略過部分)
僅4位的2進制數 快速計算方法 十進制值 十六進制
1111 = 8 + 4 + 2 + 1 = 15 =F
1110 = 8 + 4 + 2 + 0 = 14= E
1101 = 8 + 4 + 0 + 1 = 13= D
1100 = 8 + 4 + 0 + 0 = 12 =C
1011 = 8 + 0 + 2 + 1 = 11= B
1010 = 8 + 0 + 2 + 0 = 10 =A
1001 = 8 + 0 + 0 + 1 =9 =9
……
0001 = 0 + 0 + 0 + 1 = 1= 1
0000 = 0 + 0 + 0 + 0 = 0= 0
二進制數要轉換為十六進制,就是以4位一段,分別轉換為十六進制。
如(上行為二制數,下面為對應的十六進制):
1111 1101 , 1010 0101 , 1001 1011
F D , A 5 , 9 B
反過來,當我們看到 FD時,如何迅速將它轉換為二進制數呢?
先轉換F:
看到F,我們需知道它是15(可能你還不熟悉A~F這五個數),然後15如何用8421湊呢?應該是8 + 4 + 2 + 1,所以四位全為1 :1111。
接著轉換D
看到D,知道它是13,13如何用8421湊呢?應該是:8 + 4 + 1,即:1101。
所以,FD轉換為二進制數,為:1111 1101
由於十六進制轉換成二進制相當直接,所以,我們需要將一個十進制數轉換成2進制數時,也可以先轉換成16進制,然後再轉換成2進制。
比如,十進制數 1234轉換成二制數,如果要一直除以2,直接得到2進制數,需要計算較多次數。所以我們可以先除以16,得到16進制數:
被除數 計算過程 商 餘數
1234 1234/16 77 2
77 77/16 4 13 (D)
4 4/16 0 4
結果16進制為:4D2
然後我們可直接寫出4D2的二進制形式:
| 0100 | 1101 | 0010 |
其中對映關係為:
0100 -- 4
1101 -- D
0010 -- 2
同樣,如果一個二進制數很長,我們需要將它轉換成10進制數時,除了前面學過的方法是,我們還可以先將這個二進制轉換成16進制,然後再轉換為10進制。
下面舉例一個int類型的二進制數:
| 01101101 | 11100101 | 10101111 | 00011011 |
我們按四位一組轉換為16進制:6D E5 AF 1B
十進制轉十六進制
 十六進制
十六進制采餘數定理分解,例如將487710轉成十六進制:
487710÷16=30481....14(E)
30481÷16=1905....1
1905÷16=119....1
119÷16=7....7
7÷16=0....7
這樣就計到487710(10)=7711E(16)
表達方法
程式的表達方法環境 格式備註URL%hex無 XML,XHTML&#xhex無HTML,CSS#hex6位,表示顏色UnicodeU+hex6位,表示字元編碼MIME=hex無Modula-2#hex無Smalltalk,ALGOL 6816rhex無Common Lisp#xhex或#16rhex無IPv68個hex用:分隔無
C C++的表達方法
如果不使用特殊的書寫形式,16進制數也會和10進制相混。隨便一個數:9876,就看不出它是16進制或10進制。
C,C++規定,16進制數必須以 0x開頭。比如 0x1表示一個16進制數。而1則表示一個十進制。另外如:0xff,0xFF,0X102A,等等。其中的x也不區分大小寫。(注意:0x中的0是數字0,而不是字母O)
以下是一些用法示例:
int a = 0x100F;
int b = 0x70 + a;
至此,我們學完了所有進制:10進制,8進制,16進制數的表達方式。最後一點很重要,C/C++中,10進制數有正負之分,比如12表示正12,而-12表示負12,;但8進制和16進制只能表達無符號的正整數,如果你在代碼中寫:-078,或者寫:-0xF2,C,C++並不把它當成一個負數。
在轉義符中的使用
轉義符也可以接一個16進制數來表示一個字元。如 \'?\' 字元,可以有以下表達方式:
\'?\' //直接輸入字元
\'\77\' //用八進制,此時可以省略開頭的0
\'\0x3F\' //用十六進制
同樣,這一小節只用於了解。除了空字元用八進制數 \'\0\' 表示以外,我們很少用後兩種方法表示一個字元。
各碼轉換
結束了各種進制的轉換,我們來談談另一個話題:原碼、反碼、補碼。
我們已經知道計算機中,所有數據最終都是使用二進制數表達。
我們也已經學會如何將一個10進制數如何轉換為二進制數。
不過,我們仍然沒有學習一個負數如何用二進制表達。
比如,假設有一 int 類型的數,值為5,那么,我們知道它在計算機中表示為:5
| 00000000 | 00000000 | 00000000 | 00000101 |
轉換成二制是101,不過int類型的數占用4位元組(32位),所以前面填了一堆0。
想知道,-5在計算機中如何表示嗎?
在計算機中,負數以其正值的補碼形式表達。
什麼叫補碼呢?這得從原碼,反碼說起。
原碼:一個整數,按照絕對值大小轉換成的二進制數,稱為原碼。
比如
| 00000000 | 00000000 | 00000000 | 00000101 |
是 5的 原碼。
反碼:將二進制數按位取反,所得的新二進制數稱為原二進制數的反碼。
取反操作指:原為1,得0;原為0,得1。(1變0; 0變1)
比如:
| 00000000 | 00000000 | 00000000 | 00000101 |
每一位取反,得11111111 11111111 11111111 11111010。
稱:11111111 11111111 11111111 11111010 是
| 00000000 | 00000000 | 00000000 | 00000101 |
的反碼。
反碼是相互的,所以也可稱:
| 11111111 | 11111111 | 11111111 | 11111010 |
和
| 00000000 | 00000000 | 00000000 | 00000101 |
互為反碼。
補碼:反碼加1稱為補碼。
也就是說,要得到一個數的補碼,先得到反碼,然後將反碼加上1,所得數稱為補碼。
比如:
| 00000000 | 00000000 | 00000000 | 00000101 |
的反碼是:
| 11111111 | 11111111 | 11111111 | 11111010 |
那么,補碼為:
11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011
所以,-5 在計算機中表達為:11111111 11111111 11111111 11111011。轉換為十六進制:0xFFFFFFFB。
再舉一例,我們來看整數-1在計算機中如何表示。
假設這也是一個int類型,那么:
1、先取1的原碼:
| 00000000 | 00000000 | 00000000 | 00000001 |
2、得反碼:
| 11111111 | 11111111 | 11111111 | 11111110 |
3、得補碼:
| 11111111 | 11111111 | 11111111 | 11111111 |
可見,-1在計算機里用二進制表達就是全1。16進制為:0xFFFFFFFF。
一切都是紙上說的……說-1在計算機里表達為0xFFFFFFFF,我能不能親眼看一看呢?當然可以。利用C++ Builder的調試功能,我們可以看到每個變數的16進制值。
變數
下面我們來動手完成一個小小的實驗,通過調試,觀察變數的值。
我們在代碼中聲明兩個int 變數,並分別初始化為5和-5。然後我們通過CB提供的調試手段,可以查看到程式運行時,這兩個變數的十進制值和十六進制值。
首先寫一個如下的C語言控制台程式:
設定斷點:最常用的調試方法之一,使程式在運行時,暫停在某一代碼位置,
在Code::Blocks中,設定斷點的方法是在某一行代碼上按F5或在行首欄內單擊滑鼠。
我們在return 0;這一行上設定斷點。斷點所在行將被Code::Blocks以紅色顯示。
接著,運行程式(F9),程式將在斷點處停下來。
(請注意兩張圖的不同,前面的圖是運行之前,後面這張是運行中,左邊的箭頭表示運行運行到哪一行)
當程式停在斷點的時,我們可以觀察當前代碼片段內,可見的變數。觀察變數的方法很多種,這裡我們學習使用 Debug Inspector (調試期檢視),來全面觀察一個變數。
以下是調出觀察某一變數的Debug Inspector視窗的方法:
先確保代碼視窗是活動視窗。(用滑鼠點一下代碼視窗)
按下Ctrl鍵,然後將滑鼠挪到變數 aaaa 上面,你會發現代碼中的aaaa變藍,並且出現下劃線,效果如網頁中的超連結,而滑鼠也變成了小手狀:
點擊滑鼠,將出現變數aaaa的檢視視窗。
從該視窗,我可以看到:
aaaa :變數名
int :變數的數據類型
0012FF88:變數的記憶體地址,請參看5.2 變數與記憶體地址;地址總是使用十六進制表達
5 :這是變數的值,即aaaa = 5;
0x00000005 :同樣是變數的值,但採用16進制表示。因為是int類型,所以占用4位元組。
首先先關閉前面的用於觀察變數aaaa的Debug Inspector視窗。
然後,我們用同樣的方法來觀察變數bbbb,它的值為-5,負數在計算機中使用補碼錶示。
正如我們所想,-5的補碼為:0xFFFFFFFB。
再按一次F9,程式將從斷點繼續運行,然後結束。
總結
很難學的一章?
來看看我們主要學了什麼:
1、我們學會了如何將二、八、十六進制數轉換為十進制數。
三種轉換方法是一樣的,都是使用乘法。
2、我們學會了如何將十進制數轉換為二、八、十六進制數。
方法也都一樣,採用除法。
3、我們學會了如何快速的地互換二進制數和十六進制數。
要訣就在於對二進制數按四位一組地轉換成十六進制數。
在學習十六進制數後,我們會在很多地方採用十六進制數來替代二進制數。
4、我們學習了原碼、反碼、補碼。
把原碼的0變1,1變0,就得到反碼。要得到補碼,則先得反碼,然後加1。
以前我們只知道正整數在計算機里是如何表達,這時我們還知道負數在計算機里使用其絕對值的補碼錶達。
比如,-5在計算機中如何表達?回答是:5的補碼。
5、最後我們在上機實驗中,這會了如何設定斷點,如何調出Debug Inspector視窗觀察變數。
以後我們會學到更多的調試方法。
標準表示
在數制使用時,常將各種數制用簡碼來表示:如十進制數用D表示或省略;二進制用B來表示;十六進制數用H來表示。
如:十制數123表示為:123D或者123;二進制數1011表示為:1011B;十六進制數3A4表示為:3A4H。
另外在編程中十六進制數也用“0x”作為開頭。
意義
用於計算機領域的一種重要的數制。
對計算機理論的描述,計算機硬體電路的設計都是很有益的。比如邏輯電路設計中,既要考慮功能的完備,還要考慮用儘可能少的硬體,十六進制就能起到一些理論分析的作用。比如四位二進制電路,最多就是十六種狀態,也就是一種十六進制形式,只有這十六種狀態都被用上了或者儘可能多的被用上,硬體資源才發揮了儘可能大的作用。
十六進制更簡短,因為換算的時候一位16進制數可以頂4位2進制數。
你可以在二進制前加幾個0,意義不變。
| 二進制 | 八進制 | 十進制 | 十六進制 |
| 0 1 | 0 1 | 0 1 | 0 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
| 10001 | 21 | 17 | 11 |
| 10010 | 22 | 18 | 12 |
| 10011 | 23 | 19 | 13 |
| 10100 | 24 | 20 | 14 |
| 10101 | 25 | 21 | 15 |
| 10110 | 26 | 22 | 16 |
| 10111 | 27 | 23 | 17 |
| 11000 | 30 | 24 | 18 |
| 11001 | 31 | 25 | 19 |
| 11010 | 32 | 26 | 1A |
| 11011 | 33 | 27 | 1B |
| 11100 | 34 | 28 | 1C |
| 11101 | 35 | 29 | 1D |
| 11110 | 36 | 30 | 1E |
| 11111 | 37 | 31 | 1F |
| 100000 | 40 | 32 | 20 |
| 100001 | 41 | 33 | 21 |
| 100010 | 42 | 34 | 22 |
| 100011 | 43 | 35 | 23 |
| 100100 | 44 | 36 | 24 |
| 100101 | 45 | 37 | 25 |
| 100110 | 46 | 38 | 26 |
| 100111 | 47 | 39 | 27 |
| 101000 | 50 | 40 | 28 |
| 101001 | 51 | 41 | 29 |
| 101010 | 52 | 42 | 2A |
| 101011 | 53 | 43 | 2B |
| 101100 | 54 | 44 | 2C |
| 101101 | 55 | 45 | 2D |
| 101110 | 56 | 46 | 2E |
| 101111 | 57 | 47 | 2F |
| 110000 | 60 | 48 | 30 |
| 110001 | 61 | 49 | 31 |
| 110010 | 62 | 50 | 32 |
| 110011 | 63 | 51 | 33 |
| 110100 | 64 | 52 | 34 |
| 110101 | 65 | 53 | 35 |
| 110110 | 66 | 54 | 36 |
| 110111 | 67 | 55 | 37 |
| 111000 | 70 | 56 | 38 |
| 111001 | 71 | 57 | 39 |
| 111010 | 72 | 58 | 3A |
| 111011 | 73 | 59 | 3B |
| 111100 | 74 | 60 | 3C |
| 111101 | 75 | 61 | 3D |
| 111110 | 76 | 62 | 3E |
| 111111 | 77 | 63 | 3F |
| 1000000 | 100 | 64 | 40 |
| 1000001 | 101 | 65 | 41 |
| 1000010 | 102 | 66 | 42 |
| 1000011 | 103 | 67 | 43 |
| 1000100 | 104 | 68 | 44 |
| 1000101 | 105 | 69 | 45 |
| 1000110 | 106 | 70 | 46 |
| 1000111 | 107 | 71 | 47 |
| 1001000 | 110 | 72 | 48 |
| 1001001 | 111 | 73 | 49 |
| 1001010 | 112 | 74 | 4A |
| 1001011 | 113 | 75 | 4B |
| 1001100 | 114 | 76 | 4C |
| 1001101 | 115 | 77 | 4D |
| 1001110 | 116 | 78 | 4E |
| 1001111 | 117 | 79 | 4F |
| 1010000 | 120 | 80 | 50 |
| 1010001 | 121 | 81 | 51 |
| 1010010 | 122 | 82 | 52 |
| 1010011 | 123 | 83 | 53 |
| 1010100 | 124 | 84 | 54 |
| 1010101 | 125 | 85 | 55 |
| 1010110 | 126 | 86 | 56 |
| 1010111 | 127 | 87 | 57 |
| 1011000 | 130 | 88 | 58 |
| 1011001 | 131 | 89 | 59 |
| 1011010 | 132 | 90 | 5A |
| 1011011 | 133 | 91 | 5B |
| 1011100 | 134 | 92 | 5C |
| 1011101 | 135 | 93 | 5D |
| 1011110 | 136 | 94 | 5E |
| 1011111 | 137 | 95 | 5F |
| 1100000 | 140 | 96 | 60 |
| 1100001 | 141 | 97 | 61 |
| 1100010 | 142 | 98 | 62 |
| 1100011 | 143 | 99 | 63 |
| 1100100 | 144 | 100 | 64 |