平衡三進制

平衡三進制，也稱為對稱三進制，是一種以3為基數，以-1，0，1為基本數碼的三進制計數體系。俄羅斯科技人員曾經將其套用到計算機系統，目前也被套用於光子計算機相關研究中。

表示方法

整數

平衡三進制和其他進制一樣，各位的數字和位權相乘然後疊加起來，就是該數的數值。平衡三進制不需要額外的符號就可以表示負數。第一個非0位是T的為負數，第一個非0位是1的是正數。

在平衡三進制中，各位上的數字之和為偶數的整數是偶數；各位上的數字之和為奇數的整數是奇數。

我們用F表示-1，那么有：

十進制	-13	-12	-11	-10	-9	-8	-7	-6	-5
平衡三進制	FFF	FF0	FF1	F0F	F00	F01	F1F	F10	F11
二進制（8位）	1111 0011	1111 0100	1111 0101	1111 0110	1111 0111	1111 1000	1111 1001	1111 1010	1111 1011
十進制	-4	-3	-2	-1	0	1	2	3	4
平衡三進制	FF	F0	F1	F	0	1	1F	10	11
二進制（8位）	1111 1100	1111 1101	1111 1110	1111 1111	0000 0000	0000 0001	0000 0010	0000 0011	0000 0100
十進制	5	6	7	8	9	10	11	12	13
平衡三進制	1FF	1F0	1F1	10F	100	101	11F	110	111
二進制（8位）	0000 0101	0000 0110	0000 0111	0000 1000	0000 1001	0000 1010	0000 1011	0000 1100	0000 1101

從上面的表示上看，並不是嚴格意義上的逢三進一，實際上是偏置後的逢三進一。

小數

一些小數的平衡三進制表示

平衡三進制和十進制一樣，用小數點分隔整數部分和小數部分。

在平衡三進制中，四捨五入和截位的操作是等效的。

分數的小數化

分數的小數化

平衡三進制可以像十進制一樣，可以用小數來表示分數。例如⅓=0.13。

與十進制、二進制類似，部分分數有兩種表達形式。在十進制、二進制中，最小的數碼是0，因此小數點後最右邊無限循環的0可以省略掉，從而變成一個整數或有限小數；而在平衡三進制中，小數點後最右邊無限循環的T不能省略，因而不能變成整數或有限小數。

無理數

無論對於十進制、平衡三進制還是其他以有理數為底數的記數系統，所有的無理數都只能表示成無限不循環小數。

代數數	十進制	平衡三進制
平衡三進制	1.41421356237309... (≈ 1.414)	1.11T1TT00T00T01T0T00T00T01T...
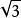平衡三進制	1.73205080756887... (≈ 1.732)	1T.T1TT10T0000TT1100T0TTT011T...
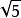平衡三進制	2.2360679774997... (≈ 2.236)	1T.1T0101010TTT1TT11010TTT01T...
φ（黃金分割， 平衡三進制 ）	1.6180339887498... (≈ 1.618)	1T.T0TT01TT0T10TT11T0011T1001...
超越無理數	十進制	平衡三進制
π（圓周率）	3.1415926535897932384626433...(≈ 3.1416)	10.011T111T000T011T1101T11111...
e（自然對數的底）	2.718281828459045... (≈ 2.718)	10.T0111TT0T0T111T0111T000T11...

轉換

十進制轉化為平衡三進制，可參照下述方法，先圓整後，再分別對整數部分和小數部分進行連除法和連乘法即可。

邏輯常量

三進制計算機，以三值邏輯為基礎，有三個邏輯常量——真、假、未知。我們用1表示真、0表示未知、T表示假。

信息的表示

三進制計算機中，以平衡三進制為信息進行編碼。

我們可以以12位為單位，對文字進行編碼作為標準信息交換碼（STUCII，Standard Ternary Unified Code for Information Interchange）。其容量為53'1441個字元，約是16bits容量的8.1倍。

運算

加減乘除四則運算

平衡三進制和二進制一樣，乘法運算等效於移位疊加運算。

加法

+	TT	T0	T1		T	0	1		1T	10	11
11	0	1	1T		10	11	1TT		1T0	1T1	10T
10	T	0	1		1T	10	11		1TT	1T0
1T	T1	T	0		1	1T	10		11
1	T0	T1	T		0	1	1T
0	TT	T0	T1		T	0	1
T	T11	TT	T0		T1	T	0
T1	T10	T11	TT
T0	T1T	T10
TT	T01

乘法

×	TT	T0	T1		T	0	1		1T	10	11
11	T11T	TT0	T01		TT	0	11		10T	110	1TT1
10	TT0	T00	T10		T0	0	10		1T0	100
1T	T01	T10	TT		1	0	IT		11
1	TT	T0	T1		T	0	1
0	0	0	0		0	0	0
T	11	10	1T		1	0	T
T1	10T	1T0	11
T0	110	100
TT	1TT1

減法

-	TT	T0	T1		T	0	1		1T	10	11
TT	0	T	T1		T0	TT	T11		T10	T1T	T01
T0	1	0	T		T1	T0	TT		T11	T10	T1T
T1	1T	1	0		T	T1	T0		TT	T11	T10
T	10	1T	1		0	T	T1		T0	TT	T11
0	11	10	1T		1	0	T		T1	T0	TT
1	1TT	11	10		1T	1	0		T	T1	T0
1T	1T0	1TT	11		10	1T	1		0	T	T1
10	1T1	1T0	1TT		11	10	1T		1	0	T
11	10T	1T1	1T0		1TT	11	10		1T	1	0

除法

÷	TT	T0	T1		T	0	1		1T	10	11
TT	1	1.1	1T		11	-∞	TT		T1	T.T	T
T0	1.T1	1	1.1		10	-∞	T0		T.T	T	T.1T
T1	1.T	1.T	1		1T	-∞	T1		T	T.1	T.1
T	0.1T	0.1	0.1		1	-∞	T		0.T	0.T	0.T1
0	0	0	0		0	NaN	0		0	0	0
1	0.T1	0.T	0.T		T	+∞	1		0.1	0.1	0.1T
1T	T.1	T.1	T		T1	+∞	1T		1	1.T	1.T
10	T.1T	T	T.T		T0	+∞	10		1.1	1	1.T1
11	T	T.T	T1		TT	+∞	11		1T	1.1	1

註：減法是左列減去頂行，除法是左列除以頂行

從上表中可以看出，雙位數相加可能會變成單位數，雙位數相減可能會變成三位數，雙位數相乘可能可能仍是雙位數。這種情況在十進制和二進制中不會發生。

邏輯運算

以下是平衡三進制邏輯運算真值表。

邏輯與

∧	T	0	1
T	T	T	T
0	T	0	0
1	T	0	1

邏輯或

∨	T	0	1
T	T	0	1
0	0	0	1
1	1	1	1

邏輯與非

↑	T	0	1
T	1	1	1
0	1	0	0
1	1	0	T

邏輯或非

↓	T	0	1
T	1	0	T
0	0	0	T
1	T	T	T

邏輯異或

⊕	T	0	1
T	T	0	1
0	0	0	0
1	1	0	T

邏輯合意

⊠	T	0	1
T	T	0	0
0	0	0	0
1	0	0	1

邏輯調和

⊞	T	0	1
T	T	T	0
0	T	0	1
1	0	1	1

邏輯非

¬	T	0	1
	1	0	T