來源
乘法是算術中最簡單的運算之一。 最早來自於整數的乘法運算。
什麼是乘法
乘法是四則運算之一
例如4乘5,就是4增加了5倍率,也可以說成5個4連加。
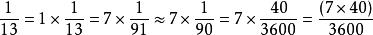 乘法
乘法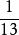 乘法
乘法古巴比倫人很早就發現,1/7是一個無限小數,怎么除也除不完。古巴比倫的倒數表里所有的數都是精確的小數,它們(在60進制中)都是有限小數。碰到無限小數時,他們會用取近似值的方法來解決。例如,古巴比倫人會通過 來計算 的值。那個40就是查倒數表查出來的。
“小九九”的由來
《九九乘法歌訣》,又常稱為“小九九”。現在學生學的“小九九”口訣,是從“一一得一”開始,到“九九八十一”止,而在古代,卻是倒過來,從“九九八十一”起,到“二二得四”止。因為口訣開頭兩個字是“九九”,所以,人們就把它簡稱為“九九”。大約到13、14世紀的時候才倒過來像現在這樣“一一得一……九九八十一”。
中國使用“九九口訣”的時間較早。在《荀子》、《管子》、《淮南子》、《戰國策》等書中就能找到“三九二十七”、“六八四十八”、“四八三十二”、“六六三十六”等句子。由此可見,早在“春秋”、“戰國”的時候,《九九乘法歌訣》就已經開始流行了。
名稱
“×”是乘號,乘號前面和後面的數叫做因數,“=”是等於號,等於號後面的數叫做積。
10(因數) ×(乘號) 200(因數) =(等於號) 2000(積)
因數也叫乘數。
讀法
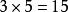 乘法
乘法讀作:三乘五等於十五
注意:現行課本中,只說“乘”不說“乘以”。要注意和除法中“除”和“除以”區分。
發展
在各種文明的算術發展過程中,乘法運算的產生是很重要的一步。一個文明可以比較順利地發展出計數方法和加減法運算,但要想創造一套簡單可行的乘法運算方法卻不那么容易。我們目前使用的乘法豎式計算看似簡便,實際上這需要我們事先掌握九九乘法口訣表;考慮到這一點,這種豎式計算並不是完美的。我們即將看到,在數學的發展過程中,不同的文明創造出了哪些不同的乘法運算方法,其中有的運算法甚至可以完全拋棄乘法表。
古巴比倫數學使用60進制,考古發現的一塊古巴比倫泥板證實了這一點。這塊泥板上有一個正方形,對角線上有四個數字1, 24, 51, 10。最初發現這塊泥板時人們並不知道這是什麼意思,後來某牛人驚訝地發現,如果把這些數字當作60進制的三位小數的話,得到的正好是單位正方形對角線長度的近似值:1 + 24/60 + 51/60^2 + 10/60^3 = 1.41421296296... 這說明古巴比倫已經掌握了勾股定理。60進制的使用為古巴比倫數學的乘法運算發展帶來了很大的障礙,因為如果你要背59-59乘法口訣表的話,至少也得背1000多項,等你把它背完了後我期末論文估計都已經全寫完了。另一項考古發現告訴了我們古巴比倫數學的乘法運算如何避免使用乘法表。考古學家們發現一些泥板上刻有60以內的平方表,利用公式ab = [(a+b)^2 - a^2 - b^2]/2 可以迅速查表得到ab的值。另一個公式則是ab = [(a+b)^2 - (a-b)^2]/4,這說明兩個數相乘只需取它們的和平方與差平方的差,再兩次取半即可。平方數的頻繁使用很可能加速了古巴比倫人發現勾股定理的過程。
古巴比倫數學把除以一個數看作是乘以它的倒數,利用倒數表可以很方便的實現這種算法。倒數表開頭的一部分是這個樣子:
2 0; 30
3 0; 20
4 0; 15
5 0; 12
6 0; 10
8 0; 7, 30
9 0; 6, 40
10 0; 6
12 0; 5
15 0; 4
16 0; 3, 45
18 0; 3, 20
20 0; 3
... ....
古巴比倫人很早就發現,1/7是一個無限小數,怎么除也除不完。古巴比倫的倒數表里所有的數都是精確的小數,它們(在60進制中)都是有限小數。碰到無限小數時,他們會用取近似值的方法來解決。例如,古巴比倫人會通過1/13 = 1*(1/13) = 7*(1/91) ≈ 7*(1/90) = 7*(40/3600) = (7*40)/3600 來計算1/13的值。那個40就是查倒數表查出來的。
古埃及數學使用了完全不同的乘法運算法。它們的乘法運算不需要藉助任何輔助用表。古埃及人注意到,任何一個數都可以表示為若干個不同的2的冪的和。因此,你需要做的僅僅是不斷將1和乘數進行翻倍。看看古埃及人如何計算46乘以22:
46 x 22 = 1012
1 22
2 44 44
4 88 + 88
8 176 + 176
16 352
32 704 + 704
-------
1012
上面的演算中,左列是1不斷翻倍的結果,右邊是22不斷翻倍的結果。選出左列的2, 4, 8, 32,它們的和正好就是被乘數46;那么把右列對應的數加起來就是乘法運算的最終結果。至於如何選出2, 4, 8, 32這四個數,一個簡單的方法就是,不斷選出左列里小於被乘數的數中最大的一個,然後當前被乘數減去它。比如,32是最大的數,用46-32後剩14;8是小於14的最大數,14-8後剩6;然後最大的小於6的數是4,6減去4後剩2,這樣下來2+4+8+32正好就是被乘數46了。這其實就是二進制的經典套用,2, 4, 8, 32正好與46的二進制中的數字1一一對應。你可以在這裡看到一些相關的東西。
計算方法
使用鉛筆和紙張乘數的常用方法需要一個小數字(通常為0到9的任意兩個數字)的存儲或查詢產品的乘法表,但是一種農民乘法算法的方法不是。
將數字乘以多於幾位小數位是繁瑣而且容易出錯的。發明了通用對數以簡化這種計算。幻燈片規則允許數字快速乘以大約三個準確度的地方。從二十世紀初開始,機械計算器,如Marchant,自動倍增多達10位數。現代電子計算機和計算器大大減少了用手倍增的需要。
歷史算法
在埃及,希臘,印度和中華文明中記載了繁殖方法。
公元前約公元前十八萬公元至二千零二十年的三叉骨,暗示了中非舊石器時代上升的知識。
埃及人
在阿姆斯紙莎草紙中記載的埃及整數和分數乘法的方法是連續添加和加倍。例如,要找到13和21的乘積,必須雙倍21次,得到2×21 = 42,4×21 = 2×42 = 84,8×21 = 2×84 = 168.完整的產品可以然後通過添加在雙倍序列中找到的適當術語來找到:
13×21 =(1 + 4 + 8)×21 =(1×21)+(4×21)+(8×21)= 21 + 84 + 168 = 273。
巴比倫人
巴比倫人使用了一個十六進制位置數字系統,類似於現代十進制。因此,巴比倫的乘法非常類似於現代十進制乘法。由於記憶60×60不同產品的相對困難,巴比倫數學家使用乘法表。這些表由某個主體號n:n,2n,...,20n的前20個倍數列表組成。其次是10n:30n 40n和50n的倍數。然後計算任何六進制產品,例如53n,只需要從表中計算出50n和3n。
中國人
在公元前300年前的數學文本《周髀算經》和《算術九章》中,乘法計算用字寫出,雖然早期的中國數學家使用了涉及加法,減法,乘法和除法的羅德微積分。 Al Khwarizmi在9世紀初向阿拉伯國家介紹了這些地名十進制算術算法。
意義
3×5表示5個3相加
5x3表示3個5相加。
注意:1.在如上乘法表示什麼中,常把乘號後面的因數做為乘號前因數的倍數。
2.參見wiki中對乘數和被乘數的定義
另: 乘法的新意義:乘法不是加法的簡單記法
Ⅰ 乘法原理:如果因變數 f與自變數 x1, x2, x3,…. xn之間存在直接正比關係並且每個自變數存在質的不同,缺少任何一個自變數因變數 f就失去其意義,則為乘法。
在機率論中,一個事件,出現結果需要分n個步驟,第1個步驟包括M1個不同的結果,第2個步驟包括M2個不同的結果,……,第n個步驟包括Mn個不同的結果。那么這個事件可能出現N=M1×M2×M3×……×Mn個不同的結果。
Ⅱ 加法原理:如果因變數 f與自變數( z1, z2, z3…, zn)之間存在直接正比關係並且每個自變數存在相同的質,缺少任何一個自變數因變數 f仍然有其意義,則為加法。
在機率論中,一個事件,出現的結果包括n類結果,第1類結果包括M1個不同的結果,第2類結果包括M2個不同的結果,……,第n類結果包括Mn個不同的結果,那么這個事件可能出現N=M1+M2+M3+……+Mn個不同的結果。
以上所說的質是按照自變數的作用來劃分的。
此原理是邏輯乘法和邏輯加法的定量表述。
法則
兩數相乘,同號得正,異號得負,並把絕對值相乘。
運算定律
整數的乘法運算滿足:交換律,結合律, 分配律,消去律。
隨著數學的發展, 運算的對象從整數發展為更一般群。
群中的乘法運算不再要求滿足交換律。 最有名的非交換例子,就是哈密爾頓發現的四元數群。 但是結合律仍然滿足。
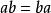 乘法
乘法1.乘法交換律: ,註:字母與字母相乘,乘號不用寫,或者可以寫成 ·。
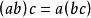 乘法
乘法2.乘法結合律: ,
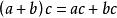 乘法
乘法3.乘法分配律: 。
其他說法
在群上再裝備另一種乘法, 則發展成為“環”, 兩種乘法中的一種可以視為傳統意義上的加法,因此要求滿足分配律和交換律;但是另一種“乘法”卻不要求交換律。
在環裡面,我們不再要求消去律成立。 如果這個環有消去律,就叫做整環。
但是對於環來說, 不一定有“除法”的概念。 如果環有除法的話,就叫做“域”。
域是最接近我們平時所說的有理數集合的東西。 但是它包含了更多信息。
結合律
前面講的這些代數對象的乘法都滿足結合律。 實際上數學發展到後來, 產生了一些不滿足結合律的乘法。
最經典的就是所謂的李(Lie)括弧
巧算
乘法是數學中基本運算之一。假設 a乘 b等於 c,即記為 ab = c或 a· b = c。
中國古代利用算籌進行乘法計算。籌算乘法分三層:上位是被乘數,中位是積,下位是乘數。先由乘數的最大一位去乘被乘數,乘完後去掉這位的算籌,再用第二位數去乘,兩次之積對應位上的數相加,乘完為止。例如81 × 81,先把乘數和被乘數分別放在上位和下位,如圖﹝a﹞。用80去乘81得6480,「8」用完了,便掉去,如圖﹝b﹞。再用1去乘81得81加到6480上,即等於6561,「1」亦用完了,便掉去,得圖﹝c﹞。
﹝a﹞﹝b﹞﹝c﹞
計算的層次就是把多位數變為用單位數去乘多位數,乘一位加一位,基本原理與現在通用的筆算乘法完全一樣,只是使用乘數的次序與現在作法相反。
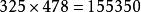 乘法
乘法中世紀,印度流行幾種實用而且有趣的乘法。「十字相乘法」是其中一種,印度人稱之為閃電似的乘法。例如
1494年義大利數學家巴切利﹝1445 - 1514﹞介紹了八種乘法。第一種乘法與現在通用的筆算乘法完全一致,第六種就是方格乘法。此法約於十五世紀傳入中國,因其圖形有如織錦﹝參看下圖﹞,故亦稱為鋪地錦。
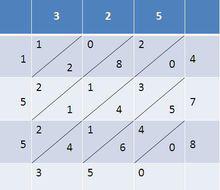 325乘478的方格乘法
325乘478的方格乘法若仔細分析上表,﹝甚至可比較「十字相乘法」之算法﹞,則可體會到這些乘法的巧妙之處。
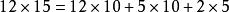 乘法
乘法這當中利用了乘法的巧算,比如:
現在人們一般把那些有心計、會算計、善謀劃的人形容為心裡有“小九九”。
乘法表
乘法表
| 1x1=1 | ||||||||
| 1x2=2 | 2x2=4 | |||||||
| 1x3=3 | 2x3=6 | 3x3=9 | ||||||
| 1x4=4 | 2x4=8 | 3x4=12 | 4x4=16 | |||||
| 1x5=5 | 2x5=10 | 3x5=15 | 4x5=20 | 5x5=25 | ||||
| 1x6=6 | 2x6=12 | 3x6=18 | 4x6=24 | 5x6=30 | 6x6=36 | |||
| 1x7=7 | 2x7=14 | 3x7=21 | 4x7=28 | 5x7=35 | 6x7=42 | 7x7=49 | ||
| 1x8=8 | 2x8=16 | 3x8=24 | 4x8=32 | 5x8=40 | 6x8=48 | 7x8=56 | 8x8=64 | |
| 1x9=9 | 2x9=18 | 3x9=27 | 4x9=36 | 5x9=45 | 6x9=54 | 7x9=63 | 8x9=72 | 9x9=81 |
口訣表
| 一一得一 | ||||||||
| 一二得二 | 二二得四 | |||||||
| 一三得三 | 二三得六 | 三三得九 | ||||||
| 一四得四 | 二四得八 | 三四十二 | 四四十六 | |||||
| 一五得五 | 二五一十 | 三五十五 | 四五二十 | 五五二十五 | ||||
| 一六得六 | 二六十二 | 三六十八 | 四六二十四 | 五六三十 | 六六三十六 | |||
| 一七得七 | 二七十四 | 三七二十一 | 四七二十八 | 五七三十五 | 六七四十二 | 七七四十九 | ||
| 一八得八 | 二八十六 | 三八二十四 | 四八三十二 | 五八四十 | 六八四十八 | 七八五十六 | 八八六十四 | |
| 一九得九 | 二九十八 | 三九二十七 | 四九三十六 | 五九四十五 | 六九五十四 | 七九六十三 | 八九七十二 | 九九八十一 |
 乘法表 圖片
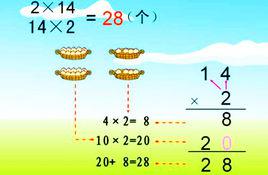
乘法表 圖片雙位乘法
個位乘以另一個因數,然後十位乘以另一個因數,最後倆者相加。
例:12×14=?
解:10*12=120
4*12=48
48+120=168