除法套用
 除法
除法若b≠0,那么
a=c/b;
若a≠0,那么
b=c/a。
如果除式的商數必須是整數,而除數和被除數並非因數關係的話,會出現相差的數值,其相差(以下的d)為餘數。
c/b=a…d
這也意味著
ab+d=c
通常不定義除以零這種形式。
特別的,當c/b作為c除以b的商出現時(此時商不為整數),或表示目前不進行除法時,c/b可以表示一個數,這種數叫做分數。此時,c/b讀作b分之c。如:10/5可理解為10除以5的商,讀作五分之十。(1/6)+(4/6)=(1+4)/6=5/6讀作六分之一加六分之四等於一加四的和除以六等於六分之五。
除法計算
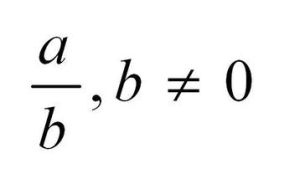 除法
除法算盤也可以做除法運算。
長除法
俗稱「長除」,適用於正式除法、小數除法、多項式除法(即
因式分解)等較重視計算過程和商數的除法,過程中兼用了乘法和減法。
長除法格式示意圖:
商數
┌───────────────────────
除數│被除數
最接近但小過或等於商數最大位或最高項與除數的積
減法────────────────────────
以上兩項之差
最接近但小過或等於商數次一位或次一項與除數的積
減法────────────────────────
以上兩項之差
最接近但小過或等於商數次二位或次二項與除數的積
減法────────────────────────
……
減法────────────────────────
餘數
短除法
俗稱「短除」,適用於快速除法、多個整數同步除法(故此常用於求出最大公因數和最低公倍數)、二進位數字轉換等較重視倍數測試和質因數(連乘式)的除法,過程大多只需用到九九乘法表及 9 以上少許整數的相乘因數。
短除法格式示意圖:
首個因數│被除數甲被除數乙
└────────────
第二因數│甲商數一乙商數一
└────────────
第三因數│甲商數二乙商數二
└────────────
最後因數│…………
└────────────
甲之終因乙之終因(其中一個已達一者或質數)……(餘數,若有的話)
計算最大公因數或最低公倍數時,因數需要是質因數。前者為左方各質因數的積,不包括底部的最終因數;後者則需要連同最終因數一起乘上。
除法的性質:
被除數連續除以兩個除數,等於除以這兩個除數之積。
除法的性質
一個數連續除以幾個數,等於這個數除以那幾個數的乘積,就是除法的性質。有時可以根據除法的性質來進行簡便運算。如:300÷25÷4=300÷(25×4)
四則運算
在初等數學中,當一級運算(加減)和二級運算(乘除)同時出現在一個式子中時,它們的運算順序是先乘除,後加減,如果有括弧就先算括弧內後算括弧外,同一級運算順序是從左到右.這樣的運算叫四則運算,.
四則指加法、減法、乘法、除法的計算法則.
一道四則運算的算式並不需要一定有四種運算符號,一般指由兩個或兩個以上運算符號及括弧,把多數合併成一個數的運算.
加法: 把兩個數合併成一個數的運算 把兩個小數合併成一個小數的運算 把兩個分數合併成一個分數的運算
減法: 已知兩個加數的和與其中一個加數,求另一個加數的運算
乘法 :求幾個相同加數的和的簡便運算 小數乘整數的意義與整數乘法意義相同
一個數乘純小數就是求這個數的十分之幾,百分之幾…… 分數乘整數的意義與整數乘法意義相同
除法: 已知兩個因數的積與其中一個因數,求另一個因數的運算 與整數除法的意義相同舉例說明:
1、乘法:①求幾個幾是多少;②求一個數的幾倍是多少;③求物體面積、體積;④求一個數的幾分之幾或百分之幾是多少。
2、除法:①把一個數平均分成若干份,求其中的一份;②求一個數里有幾個另一個數;③已知一個數的幾分之幾或百分之幾是多少求這個數。
3、加法:①求和;②減法逆運算。
4、減法:①求剩餘;②比較;③加法逆運算。
加減互為逆運算;乘除互為逆運算;乘法是加法的簡便運算。
公式
被除數÷除數=商被除數÷商=除數
商除數=被除數
還有一種情況:
被除數÷除數=商......(六點)餘數(不大於除數)
除數×商+餘數=被除數
關係
被除數擴大(縮小)n倍,商也相應的擴大(縮小)n倍。
除數擴大(縮小)n倍,商相應的縮小(擴大)n倍。

