著名定理
梅內勞斯定理
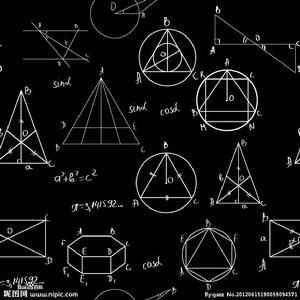
亞歷山大里亞的梅內勞斯(Menelaus,約公元100年,他和斯巴達的Menelaus是兩個人)曾著《球面論》,著重討論球面三角形的幾何性質.以他的名子命名的“梅內勞斯定理”現載在初等幾何和射影幾何的書中,是證明點共線的重要定理.
定理 一直線與△ABC的三邊AB,BC,CA或延長線分別相交於X,Y,Z,則
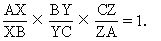 平面幾何
平面幾何義大利數學家塞瓦(G.Ceva)在1678年發表了下面的十分有用的定理,它是證明共點線的重要定理.
定理 在△ABC內任取一點P,直線AP,BP,CP分別與邊BC,CA,AB相交於D,E,F,則
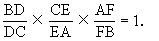 平面幾何
平面幾何定理 △ABC的邊BC上任取一點D,若BD=u,DC=v,AD=t,則
 平面幾何
平面幾何托勒密定理
托勒密(Ptolemy,約公元85~165年)是古代天文學的集大成者.一般幾何教科書中的“托勒密定理”(圓內接四邊形的對邊積之和等於對角線之積),實出自依巴谷(Hipparchus)之手,托勒密只是從他的書中摘出。從這個定理可以推出正弦、餘弦的和差公式及一系列的三角恆等式,托勒密定理實質上是關於共圓性的基本性質。
定理 如果四邊形內接於圓,那么它的兩對對邊的乘積之和等於它的對角線的乘積.
斯泰納-萊默斯定理
莫萊定理
相似命題
1, 平面中,周長相等的正三角形,正方形,圓的面積為 , , ,則 < < ;空間中,全面積相等的正四面體,正方體,球的體積為 , , ,則 < < 。這兩個命題中,周長在空間中對應全面積,正三角形對應正四面體,正方形對應正方體,圓對應球體。換言之,平面中,周長一定時,越接近圓形的圖形面積最大;空間中,全面積一定時,越接近球形的空間圖形,體積越大。
2,平面中,面積相等的正三角形,正方形,圓的周長為 , , ,則 > > 空間中,體積相等的正四面體,正方體,球的表面積為 , , ,則 > > 。換言之,平面中,面積一定時,越接近圓的圖形周長最小;空間中,體積一定時,越接近球的空間圖形,表面積越小。這也反映了宇宙中星體為什麼大多以球體或接近球體的形式存在,因為球體的表面積最小,表面積越小越穩定;動物世界中,弱小動物遇到敵人時,縮成一團,是出於本能,將受攻擊的區域減少到最小,因為球形的表面積最小。
3, 平面中,不共線的三點可確定一個圓;空間中,不共面的四點可確定一個球。
4, 平面中,過平面外一點有且只有一條直線與已知直線平行;空間中,過平面外的一條平行直線有且只有一個平面與已知平面平行。
5, 平面中,過一點有且只有一條直線與已知直線垂直;空間中,過一條直線有且只有一個平面與已知平面垂直。 6,平面中的勾股定理也可推廣到空間:(1)長方體的體對角線長的平方等於共頂點的三條棱長的平方和;(2)設三稜錐A—BCD的三個側面兩兩互相垂直,則有等式 + + = 恆成立。
7,平面中,等邊ΔABC內任一點到各邊的距離之和為定值(等邊ΔABC的高);等腰ΔABC底邊上任一點到兩腰的距離之和為定值(一腰上的高)。空間中,正四面體內任一點到各面的距離之和為定值(正四面體的高);正三稜錐底面上任一點到各側面的距離之和為定值(一側面上的高)。
8,圓的周長公式: ;球的表面積公式: ;圓的面積公式: ;球的體積公式: 。其中R表示半徑,的指數1,2以及係數 與維數之間存在著一種對應。因為平面是二維的,空間是三維的。
9,平面中,三角形被平行於它一邊的直線所截得的三角形與原三角形的面積的比等於對應邊的平方比;空間中,稜錐被平行於它低面的平面所截得的小稜錐與原稜錐的體積的比等於對應邊的立方比。
10,平面中,三角形的面積公式: ;空間中有兩個相似命題:(1)稜錐的體積公式; 。其中, 分別表示三角形的邊,稜錐的低面積, 表示高。(2)三稜錐的體積也可按此公式計算: ,其中, 為三稜錐一個側面的面積, 為該側面與所對的側棱間的距離。
11,平面中,梯形的面積公式: ;空間中,低面是梯形的直棱住的體積公式: ,其中, 表示兩個平行側面的面積, 表示這兩個側面間的距離。