性質
1． 底面是等邊三角形。
2． 側面是三個全等的等腰三角形。
3． 頂點在底面的射影是底面三角形的中心（也是重心、垂心、外心、內心）。
4. 常構造以下四個直角三角形（見圖）：
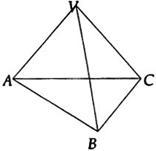正三稜錐V-ABC（2）高、斜高、斜高射影構成的直角三角形；（含側面與底面夾角）
（3）高、側棱、側棱射影構成的直角三角形；（含側棱與底面夾角）
（4）斜高射影、側棱射影、底邊的一半構成的直角三角形。
說明：上述直角三角形集中了正三稜錐幾乎所有元素。在正三稜錐計算題中，常常取上述直角三角形。其實質是，不僅使空間問題平面化，而且使平面問題三角化，還使已知元素與未知元素集中於一個直角三角形中，利於解出。
相關計算
基本公式
h為底高（法線長度）， A為底面面積， V為體積，L為斜高，C為稜錐底面周長有：三稜錐稜錐的側面展開圖是由4個三角形組成的，展開圖的面積，就是稜錐的側面積，則 ：(其中 S i, i= 1,2為第i個側面的面積）S全=S稜錐側+S底S正三稜錐=1/2CL+S底V=1/3 A(底面積)* h
三稜錐體積公式證明
如圖，這是一個一般的三稜柱ABC-A'B'C'，它的體積可以分為三個等體積的三稜錐，即三稜錐C-A'AB，三稜錐C-A'B'B，三稜錐A'-CB'C'.因為三稜柱的側面A'ABB'是平行四邊形，所以△A'AB的面積=△A'BB'的面積，即其中三稜錐C-A'AB與三稜錐C-A'B'B的底面積相等，它們兩個的頂點都是C，即C到它們底面的距離都相等，所以三稜錐C-A'AB與三稜錐C-A'B'B的體積相等。而三稜錐C-A'B'B也可以看作是三稜錐A'-BCB'，且三稜錐A'-CB'C'與三稜錐A'-BCB'的底面積相等（即△BCB'與△B'C'C的面積相等），且它們兩個的頂點都是A'，即A'到它們底面的距離都相等，所以三稜錐A'-CB'C'與三稜錐A'-BCB'的體積也相等，故三稜錐C-A'AB，三稜錐C-A'B'B，三稜錐A'-CB'C'的體積都相等，由此可見，一個三稜柱的體積等於三個等體積的三稜錐體積之和，即V三稜錐=1/3S·h.2三稜錐公式
海倫秦九韶體積公式
已知三稜錐棱長求其體積的體積公式。
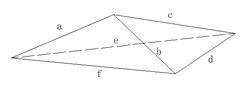正三稜錐任意一個三稜錐或者說四面體，其棱為a，b，c，d，e，f，其中a與d，b與e，c與f互為對邊，那么有三稜錐（四面體）的體積公式為
正三稜錐正四面體內切球心
內切球心在頂點與底面重心的連線的距底面1/4處
相關計算：
因為正四面體底面為正三角形，所以斜高線位於任意頂點與底邊中點連線，又三線合一，所以側面重心位於高線距頂點2/3處，即可算出頂點與重心（球與側面切點）的距離，又知正三稜錐邊長，即可根據勾股定理算出圓心所在直線（即頂點與底面重心的連線）的長度，即可算出底面與球心的距離（即內切球半徑）。
正四面體外接球心
外接球心在頂點與底面重心的連線的距頂點3/4處
相關計算：
和計算內切球心一樣算出圓心所在直線（即頂點與底面重心的連線）的長度，即可算出頂點與球心的距離（即外接球半徑）。
補充高考可能用到的數據（如圖）：
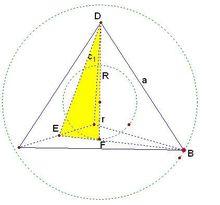正三稜錐對於棱長為a的正四面體，有：1、側面高（斜高）為（a√3）/2
2、高為（a√6）/3
3、內切球半徑（a√6）/12
4、外接球半徑（a√6）/4
