積分幾何學
正文
通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終和幾何機率聯繫著。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。常曲率空間的積分幾何 主要有以下幾種:
歐氏平面的積分幾何 每個積分都和一定的密度和測度相聯繫。例如,在歐氏平面E2上,若(x,y)為一點P的直角坐標,則區域D上的二重積分
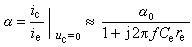 里的二次微分式dxdy 就是點密度,而當ƒ(x,y)=1時,這積分就等於D 的面積,也就是D 作為點的集合的測度。若把點密度用外微分式dP=dx∧dy表示,則上述積分就可以寫成與坐標系無關的形式
里的二次微分式dxdy 就是點密度,而當ƒ(x,y)=1時,這積分就等於D 的面積,也就是D 作為點的集合的測度。若把點密度用外微分式dP=dx∧dy表示,則上述積分就可以寫成與坐標系無關的形式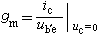 。點密度在極坐標(r,θ)下的表達式dP=rdr∧dθ。容易證明,這個點密度經過剛體運動不變,而且除一個常數因子外,它是E2上惟一的不變點密度。
。點密度在極坐標(r,θ)下的表達式dP=rdr∧dθ。容易證明,這個點密度經過剛體運動不變,而且除一個常數因子外,它是E2上惟一的不變點密度。 在E2上,一個典型的,和點密度相聯繫的克羅夫頓積分公式是
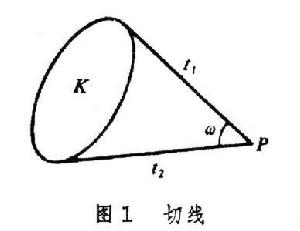 積分幾何學
積分幾何學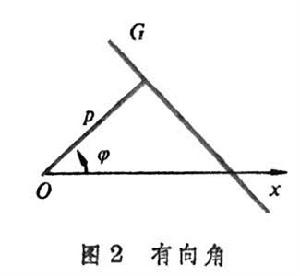 積分幾何學
積分幾何學歐氏平面上也有不變直線密度。設p是從坐標原點O到直線G 的垂直距離(p≥0),φ是由O到G 的垂線同坐標橫軸所作的有向角(0≤φ<2π)(圖2),則直線密度dG=dp∧dφ。與直線密度相聯繫的一個著名的克羅夫頓公式是
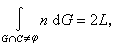
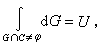
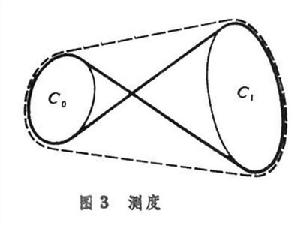 中的粗線長減去虛線長。
中的粗線長減去虛線長。 把E2上的點密度和直線密度作種種不同的結合,就得到點偶(P1,P2),線偶(G1,G2),點線(P,G),以及三點組(P1,P2,P3)等等的幾何對象的密度,並推得許多積分公式。例如,若σ 是閉凸線C 在直線上的弦長,則M.W.克羅夫頓給出了
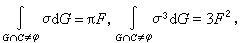
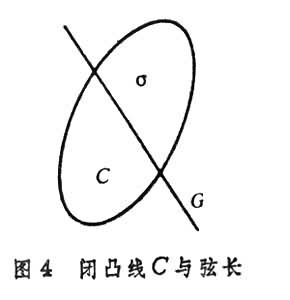 積分幾何學
積分幾何學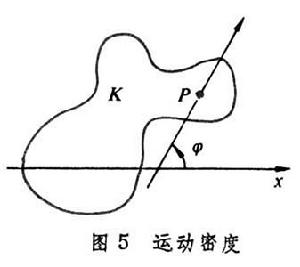 積分幾何學
積分幾何學
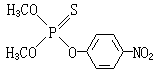

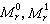 是積分不變數;ⅹ(D0),ⅹ(D1),ⅹ(D0∩D1)是拓撲不變數;Om是通用常數;dK1是K1的運動密度。具體地,Vi表示Di的n維體積,M
是積分不變數;ⅹ(D0),ⅹ(D1),ⅹ(D0∩D1)是拓撲不變數;Om是通用常數;dK1是K1的運動密度。具體地,Vi表示Di的n維體積,M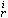 表示Di的邊界(超曲面)的第 r箇中曲率積分(i=0,1),ⅹ(D)表示區域D的歐拉-龐加萊示性數,
表示Di的邊界(超曲面)的第 r箇中曲率積分(i=0,1),ⅹ(D)表示區域D的歐拉-龐加萊示性數, 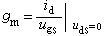 是 m維單位球的m-1維表面積。一個超曲面的所謂第r個曲率積分為
是 m維單位球的m-1維表面積。一個超曲面的所謂第r個曲率積分為 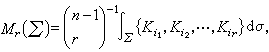
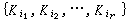 表示∑的主曲率的第 r個初等對稱函式,dσ表示∑的n-1維面積元素。
表示∑的主曲率的第 r個初等對稱函式,dσ表示∑的n-1維面積元素。 非歐空間的積分幾何 把歐氏空間的積分幾何的基本概念推廣到非歐空間,就可以建立非歐積分幾何,L.A桑塔洛推得了n維非歐空間運動主要公式。
齊性空間的積分幾何 歐氏(和非歐)空間積分幾何的基本概念還可以推廣到滿足一定條件的齊性空間。已給微分流形M,若有一個李變換群
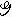 可遷地作用於M上(即對於M上任意兩點P,P′,總有
可遷地作用於M上(即對於M上任意兩點P,P′,總有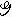 里的一個變換,把P 變成 P′),則M就成為具有變換群
里的一個變換,把P 變成 P′),則M就成為具有變換群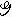 的齊性空間,再設在M里有一個圖形的集合S,在
的齊性空間,再設在M里有一個圖形的集合S,在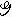 的作用下不變(即在
的作用下不變(即在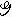 的任意一個變換的作用下,S里的一切圖形只是經歷一個置換)。例如歐氏平面E2對於運動群就是齊性空間,S可以是E2上一切點或一切直線的集合,也可以是一個互相全等的橢圓的集合,等等。這樣,在一種確定條件下,S里的圖形F 就有在
的任意一個變換的作用下,S里的一切圖形只是經歷一個置換)。例如歐氏平面E2對於運動群就是齊性空間,S可以是E2上一切點或一切直線的集合,也可以是一個互相全等的橢圓的集合,等等。這樣,在一種確定條件下,S里的圖形F 就有在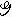 下不變的密度dF, 而且除一個常數因子外,它是惟一的。這時,若S1是S的一個子集而ƒ(F)是S1上的函式,積分
下不變的密度dF, 而且除一個常數因子外,它是惟一的。這時,若S1是S的一個子集而ƒ(F)是S1上的函式,積分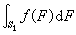 就完全確定。
就完全確定。 若Г是李變換群
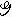 的離散子群,則商群
的離散子群,則商群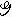 /Г是齊性空間。C.L.齊格爾把這個事實套用於 n維仿射空間里的齊次麼模(或特殊)仿射變換群和格的集合,證明了“數的幾何”中著名的閔科夫斯基-拉夫卡定理。
/Г是齊性空間。C.L.齊格爾把這個事實套用於 n維仿射空間里的齊次麼模(或特殊)仿射變換群和格的集合,證明了“數的幾何”中著名的閔科夫斯基-拉夫卡定理。 研究動向 關於齊性空間積分幾何的一般原理已富有成效地用於埃爾米特幾何學和辛幾何學。但這些方面的工作仍有待於繼續展開。
運用葉層空間的理論,可以對齊性黎曼空間中一些短程線集合和點集合引進具有某種不變性的密度,並得到一些積分公式和結果,其中有些是常曲率空間結果的推廣。
近20年來,求一種拉東變換的逆變換的課題也納入了積分幾何範疇。設 X為微分流形,M(u)是X的一族子流形,它們依賴於參數u1,u2,…,un,dσ(u)是M(u)上適當選定的微分齊式。已給X上的函式ƒ(x)(x∈X),令
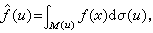
簡史 幾何機率的研究要以有關的圖形集合的測度為基礎,因而自然要導致積分幾何的建立。一般認為,最早的幾何機率問題是 G.-L.L.de布豐提出並解決的投針問題:設在平面上有一組平行線,其行距都等於D;把一根長度l<D的針隨機地投上去,則這根針和一條直線相交的機率是2l/πD。到19世紀下半葉,克羅夫頓已獲得了一系列的積分公式;它們至今仍然是積分幾何中很基本的公式,其特點是概括性高而推導簡潔。但就在此時,J.L.F.貝特朗卻發現,對於同一個幾何機率問題,對有關測度的不同要求會導致互相矛盾的解答。後來H.龐加萊指出,只須要求所採用的測度在一定變換群下不變,那樣的矛盾就不會出現。從此,幾何機率同變換群相結合,形成了積分幾何的理論基礎,成果日漸豐富。1935年起,布拉施克及其合作者在“積分幾何”這個總標題下發表了一系列論文,積分幾何就開始作為幾何的一個分支獲得了系統而深入的發展。其中,陳省身作出了卓越的貢獻,齊性空間積分幾何的理論就是他和A.韋伊建立起來的。在齊性空間裡,他引進了一種較一般的關聯概念,並在此基礎上獲得了克羅夫頓公式的一種推廣,他還推得了En里緊緻流形的一般運動公式,作為運動主要公式的補充。桑塔洛是布拉施克最早的合作者之一,他畢生致力於積分幾何的研究,時間最長,成果廣泛而豐富,所著《積分幾何與幾何機率》一書是迄今為止這方面最完備的專著。
中國較早從事積分幾何研究的還有吳大任,他第一次把歐氏空間積分幾何的基本成果(包括運動主要公式在內),推廣到三維橢圓空間。他還證明了關於E2和E3里凸體弦冪積分的一系列不等式。中國學者還獲得了其他若干成果,例如,任德麟推得了n維歐氏空間和非歐空間裡含在一個凸體內的定長線段測度公式,把關於弦冪積分的不等式推廣到En,並且推廣了布豐投針問題。
由於積分幾何是和機率以及統計緊密聯繫著的,它在許多學科(如生物學、醫學、礦物學、金屬學,以至物理、天文、建築、聲學等)中都有套用。隨著電子計算機性能的迅速提高,使用的日益廣泛,這種套用正方興未艾。已經出現了“隨機幾何學”和“數理生態學”這樣的學科名稱。這方面,所採用的方法之一是所謂的立體度測法:簡單地說,有些幾何對象的立體性質只能通過對它們的直線截痕或平面截痕的大量觀測來推算,積分幾何就在這裡提供了理想的工具。
參考書目
W.Blaschke,Vorlesungen ╇ber Integralgeometrie,Aufl.3,Deutscher Verlag der Wissenschaften,Berlin, 1955.
M.G.Kendall and P.A.P.Moran,Geometrical Probability,Griffin, London, 1963.
L.A.Santal圝,Integral Geometry and Geometric Probability,Addison-Wesley, Reading, Mass.,1976.