簡介
 點斜式方程
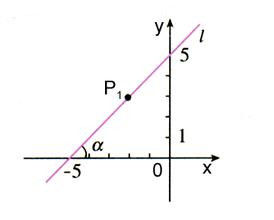
點斜式方程一般地,在平面直角坐標系中,如果直線L經過點A(X1,Y1)和B(X2,Y2),其中x1≠x2,那么AB=(x2-x1,y2-y1)是L的一個方向向量,於是直線L的斜率k=(y2-y1)/(x2-x1),再由k=tanα(0≤α<π),可求出直線L的傾斜角α.
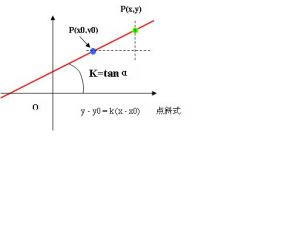
記tanα=k,方程y-y0=k(x-x0)叫做直線的點斜式方程。
當α為π/2即(90度,直線與X軸垂直)時,tanα無意義,不存在點斜式方程
點斜式方程普遍用於導數當中,用已知切線上一點和曲線方程的導數(方程上某點切線的斜率)求切線方程時用。
適用於知道一個點的坐標和直線斜率,求直線方程的題目。
方程公式
方程式:y-y1=k(x-x1)其中(x1,y1)為坐標繫上過直線的一點的坐標,k為該直線的斜率。
推導:若直線L1經過點P1(x1,y1),且斜率為k,求L1方程。
設點P(x,y)是直線上不同於點P1的任意一點,根據經過兩點的直線的斜率公式得k=(y-y1)/(x-x1)(且:x≠x1)
所以,直線L1:y-y1=k(x-x1)
說明:(1)這個方程是由直線上一點和斜率確定的,這一點必須在直線上,否則點斜式方程不成立;
(2)當直線l的傾斜角為0°時,直線方程為y=y1;
(3)當直線傾斜角為90°時,直線沒有斜率,它的方程不能用點斜式表示,這時直線方程為x=x1。
用途
開始學習時通常是求兩條斜率不相等(非平行)的直線的交點,接著是與拋物線的交點,通過點斜式方程代入拋物線方程,求出交點的個數和坐標。還有平面解析幾何,比如橢圓、圓、雙曲線、拋物線等圓錐曲線問題解決的固定套路,方程聯立的時候就習慣用點斜式。在求曲線切線方程中,一般會告訴切點和曲線方程。這時利用導數公式可求出切線斜率k,利用點斜式可以表示此直線方程。
另外,有時題目會告訴曲線外一點(a,b)和曲線方程,這時只需設切點坐標A(x,y),利用導數公式求出導數的表達式M,再使y-b/x-a=M即可求出切點A的坐標。利用點斜式可將方程表示出來。