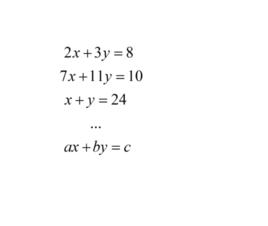定義
含有兩個未知數，並且含有未知數的項的次數都是1的整式方程叫做二元一次方程，可化為ax+by+c=0（a、b≠0）的一般式與ax+by=c（a、b≠0）的標準式。
解方程
適合一個二元一次方程的每一對未知數的值，叫做這個二元一次方程的一個解。對於任何一個二元一次方程，令其中一個未知數取任意一個值，都能求出與它對應的另一個未知數的值。因此，任何一個二元一次方程都有無數多個解，由這些解組成的集合，叫做這個二元一次方程的解集。
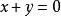二元一次方程例如，二元一次方程： ，解有無數個
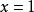二元一次方程
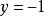二元一次方程當 時，
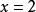二元一次方程
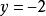二元一次方程當 時，
...
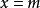二元一次方程
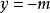二元一次方程當 時，
二元一次方程組的解
二元一次方程組中各個方程的公共解，叫做一組二元一次方程組的解。二元一次方程組通常有唯一解，但有時有無數解，有時無解，例如
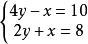二元一次方程有唯一解：
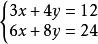二元一次方程有無數解：
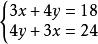二元一次方程無解：
整數解：二元一次方程的整數解就是一個二元一次方程的解均為整數的解。
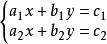二元一次方程
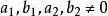二元一次方程一般解推導：設方程組 ，( )求解該方程組的解。
將方程組變形，得到：
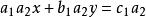二元一次方程
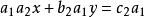二元一次方程
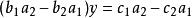二元一次方程兩式相減，得：
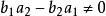二元一次方程（1）若 ，則移相，得：
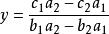二元一次方程 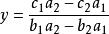二元一次方程
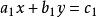二元一次方程將 代入 中，求得：
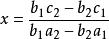二元一次方程
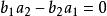二元一次方程
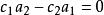二元一次方程（2）若 且 ，則y有無數解，故方程組有無數解。
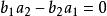二元一次方程
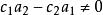二元一次方程（3）若 且 ，則y無解，故方程組無解。
求解
消元思想
“消元”是解二元一次方程組的基本思路。所謂“消元”就是減少未知數的個數，使多元方程最終轉化為一元多次方程再解出未知數。這種將方程組中的未知數個數由多化少，逐一解決的解法，叫做消元解法。
消元方法一般分為：代入消元法，簡稱：代入法 ；加減消元法，簡稱：加減法 ；順序消元法 ；整體代入法。
代入消元法
將方程組中一個方程的某個未知數用含有另一個未知數的代數式表示出來，代入另一個方程中，消去一個未知數，得到一個一元一次方程，最後求得方程組的解，這種解方程組的方法叫做代入消元法。
用代入消元法解二元一次方程組的一般步驟：
（1）等量代換：從方程組中選一個係數比較簡單的方程，將這個方程中的一個未知數（例如y），用另一個未知數（如x）的代數式表示出來，即將方程寫成y=ax+b的形式；
（2）代入消元：將y=ax+b代入另一個方程中，消去y，得到一個關於x的一元一次方程；
（3）解這個一元一次方程，求出x的值；
（4）回代：把求得的x的值代入y=ax+b中求出y的值，從而得出方程組的解；
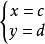二元一次方程（5）把這個方程組的解寫成 的形式．
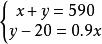二元一次方程例如：解方程組
解：
對方程進行標號：
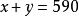二元一次方程①
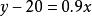二元一次方程②
由②得：
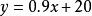二元一次方程③
把③代入①得：
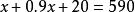二元一次方程化簡得：
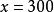二元一次方程 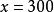二元一次方程
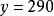二元一次方程將 代入①中，得：
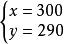二元一次方程故原方程組的解為：
加減法
當方程中兩個方程的某一未知數的係數相等或互為相反數時，把這兩個方程的兩邊相加或相減來消去這個未知數，從而將二元一次方程化為一元一次方程，最後求得方程組的解，這種解方程組的方法叫做加減消元法。
用加減消元法解二元一次方程組的一般步驟：
（1）變換係數：利用等式的基本性質，把一個方程或者兩個方程的兩邊都乘以適當的數，使兩個方程里的某一個未知數的係數互為相反數或相等；
（2）加減消元：把兩個方程的兩邊分別相加或相減，消去一個未知數，得到一個一元一次方程；
（3）解這個一元一次方程，求得一個未知數的值；
（4）回代：將求出的未知數的值代入原方程組的任何一個方程中，求出另一個未知數的值；
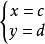二元一次方程（5）把這個方程組的解寫成 的形式．
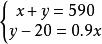二元一次方程例如：解方程組
解：對方程進行標號：
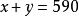二元一次方程①
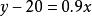二元一次方程②
由②得：
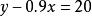二元一次方程③
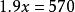二元一次方程 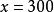二元一次方程①-③，得： ，
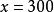二元一次方程 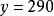二元一次方程將 代入①中，得：
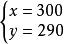二元一次方程故原方程組的解為：
換元法
解一些複雜的問題，常用到換元法，即對結構比較複雜的多項式，若把其中某些部分看成一個整體，用新字母代替(即換元)，則能使複雜的問題簡單化，明朗化。該方法在減少多項式項數，降低多項式結構複雜程度等方面能起到獨到作用。
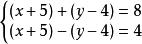二元一次方程例如：解方程
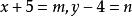二元一次方程解：設
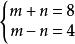二元一次方程原方程組可變為
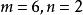二元一次方程運用加減法可解得：
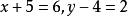二元一次方程所以
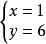二元一次方程所以 是原方程組的解.
特點：兩方程中都含有相同的代數式，如題中的x+5，y-4之類，換元後可簡化方程。
套用題
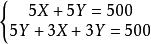二元一次方程1）A、B兩地相距500千米，甲、乙兩車由兩地相向而行，若同時出發則5小時相遇；若乙先出發5小時，則甲出發後3小時與乙相遇。求甲乙兩車速度。
解： 設甲車速度為X km/h，乙車速度為Y km/h，列方程
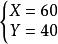二元一次方程解得
答：甲車速度為60km/h，乙車速度為40km/h。
2）兩個物體在周長等於100米的圓上運動，如果同向運動，那么它們每隔20秒相遇一次；如果相向運動，那么它們每隔5秒相遇一次。求每個物體的速度。
解：設速度快的速度為Xm/s，慢的為Y m/s，列方程
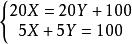二元一次方程
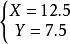二元一次方程解得
答：速度快的為12.5m/s，速度慢的為7.5m/s。
