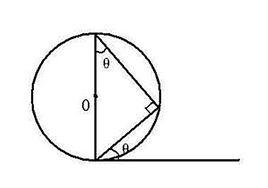
定義
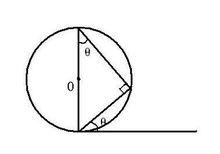弦切角頂點在圓上，一邊和圓相交，另一邊和圓相切的角叫做 弦切角。
特徵識別
①頂點在圓上；
②一條邊與圓周相交，另一條邊與圓相切，切點在圓周上；
③弦切角的大小等於它所夾的弧所對的圓周角的大小。
弦切角定理
弦切角等於它所夾的弧所對的 圓周角 。
推論1：弦切角等於它所夾的弧所對的圓心角的一半。
推論2：兩個弦切角所夾的弧相等，那么這兩個弦切角也相等。
推論3：弦切角等於它所夾的弧的度數的一半。
弦切角定理的證明：
如圖2，AB為圓O的切線，因為BD是直徑，所以內接三角形BCD是直角三角形，其中∠DCB是直角
所以∠BDC+∠1=90°
又因為∠1 +∠CBA=90°
所以∠CBA=∠BDC.
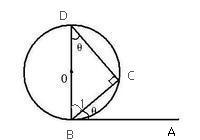圖2套用
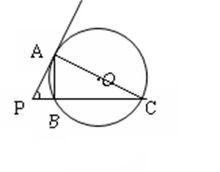弦切角已知PA為圓O的切線， A為切點， PC與⊙ O相交於 B． C兩點，求證：PA^2=PB×PC。
證明：∵∠PAB為弦切角
∴∠PAB=∠C
又∵∠P=∠P
∴△PAB∽△PCA
∴PA∶PC=PB∶PA
即PA^2=PC·PB
