數學不等式
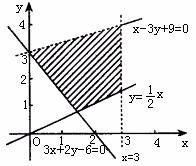
滿足二元一次不等式(組)的x和y的取值構成有序數對(x，y)，所有這樣的有序數對(x，y)構成的集合稱為二元一次不等式(組)的解集。有序實數對可以看成直角坐標平面內點的坐標。於是二元一次不等式(組)的解集就可以看成直角坐標系內的點構成的集合。
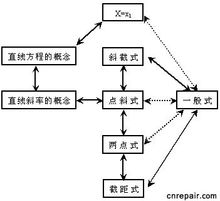直線與二元一次方程一般地， 在直角坐標系中，二元一次不等式 表示 某側所有點組成的平面區域。我們把
直線畫成虛線時，表示區域不包括邊界。而不等式 表示區域包括邊界時，則把邊界畫成實線：不等式組表示的平面區域是各個不等式所表示的平麵點集的交集，因而是各個不等式所表示的平面區域的公共部分。
第六章
二元一次不等式 6.0 小回顧
A. 一元一次不等式
B. 解聯立二元一次方程
6.1 二元一次不等式
6.2 聯立二元一次不等式
A. 解複合一元線性不等式
B. 利用圖像解聯立二元一次不等式
6.3 線性規劃
A. 二元線性函式的極值
B. 線性規劃的套用
6.0 小回顧A. 一元一次不等式 (參閱5A冊_第六章，頁278。)
二元一次不等式1.判斷下列句子是否正確。
正確 錯誤
(a)若 2x> –12，則x> –6。
(b)若x+11>0 ，則x> –11。
(c)若 a< 2 < b，則(a– 2)(b– 2) < 0。
(d)若 a> b及 c> d，則a– c> b– d。
(e)若 a> b，則a– 4 > b– 4。
(f)若 a> 0 > b，則a> b。
B. 解聯立二元一次方程(參閱5A冊_第六章，頁278 – 279。)
1. 利用代入法，解下列各聯立方程。
(a) 對所有實數 x，2(x– 3) + 9 9 。
(b) 若 4x< 3x，則x< 0。
2. 解下列各不等式，並將答案表示在數線上。
(a) 3x– 1 < 14 (b) 15 – 4x< –1
(c) 2(x+ 3) > 12 (d) –3(x– 1) –9
