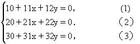萊布尼茨方程

萊布尼茨方程，數學公式之一，是以萊布尼茨的名字命名的，現已廣泛套用與數學之中。

萊布尼茨方程,即常微分方程y'=x^2+y^2.語言表述為"求這樣一個函式,它的導數等於自變數與因變數的平方和".
萊布尼茨，G．W．(Leibniz，Gottfried Wilhelm)1646年7月1日(儒略曆，1646年6月21日)生於德國萊比錫；1716年11月14日卒於德國漢諾瓦．數學、科學、哲學．
萊布尼茨出身書香門第，父親弗里德里希·萊布尼茨(Frie-drich Leibniz，1597—1652)是萊比錫大學的道德哲學教授，母親凱薩琳娜·施馬克(Katherina schmuck，1621—1664)出身教授家庭，虔信路德新教．父母親自做孩子的啟蒙教師，耳濡目染，使萊布尼茨從小就十分好學．他最先是對詩歌和歷史有著濃厚的興趣．父親在他6歲時去世了，留給他十分豐富的藏書．知書達理的母親擔負起兒子的幼年教育．萊布尼茨8歲時入尼古拉學校，學習拉丁文、希臘文、修辭學、算術、邏輯、音樂以及聖詩、路德教義等，對邏輯學很感興趣．他不滿足學校所學的內容，充分利用家中的藏書，廣泛接觸了古希臘羅馬文化，閱讀了許多著名學者的著作．13歲時，他就試圖改進亞里士多德(Aristotle)的範疇理論．
1661年，萊布尼茨進入萊比錫大學學習法律，剛一進校就跟上了大學二年級標準的人文學科的課程，還抓緊時間學習哲學和科學，廣泛地閱讀了F．培根(Bacon)、J．開卜勒(Kepler)、G．伽利略(Galileo)等人的著作，並且對前人的著述進行深入的思考和評價．1663年5月，他以題目為“論個體原則方面的形上學爭論”(Disputatio Metaphysica de principio Indiuidui)的論文獲學士學位．
1663年夏季，萊布尼茨前往耶拿大學，跟隨E．魏格爾(Weigel)系統地學習了歐氏幾何，使他開始確信畢達哥拉斯-柏拉圖(Pythagoras-Plato)宇宙觀：宇宙是一個由數學和邏輯原則所統率的和諧的整體．
1664年1月，萊布尼茨寫出論文“論法學之艱難”(Specimendifficultatis in lure)，獲哲學碩士學位．是年2月12日，他18歲時母親去世了．他一生在思想、性格方面受母親影響頗深．
從1665年開始，萊比錫大學審查他提交的博士論文“論身份”(De Conditionibus)，但1666年以他太年輕(年僅20歲)為由而拒絕授予他法學博士學位．對此他很氣憤，毅然離開萊比錫前往紐倫堡附近的阿爾特多夫大學，並立即向學校提交了早已準備好的那篇博士論文，1667年2月該大學授予他法學博士學位，還聘請他為法學教授．但是他拒絕了，決心投身到外部世界，去乾更有意義的事情．萊布尼茨在紐倫堡加入了一個鍊金術士團體．1667年，通過該團體結識了政界人物博因堡男爵約翰·克里斯蒂安(Johann Choristian，Freiherr Von Boyneburg，1622—1672)，並經男爵推薦給邁因茨選帝侯J．D．馮·舍恩博恩(von Schnborn)，從此萊布尼茨登上了政治舞台．
1669年，通過閱讀英國皇家學會《會刊》(Philosophical Tran-sactions)，萊布尼茨了解到C．U．惠更斯(Huygens)正在與別人討論有關碰撞問題，促使他開始思考自然哲學問題．
從1671年開始，萊布尼茨利用外交活動開拓了與外界的廣泛聯繫，尤以通信作為他獲取外界情況、與人進行思想交流的一種主要方式．從這一年起，他與英國皇家學會秘書亨利·奧頓伯格(Henry Oldenburg)，以及巴黎科學院的著名學者們書信往來長達幾十年．
1671—1672年冬季，萊布尼茨受邁因茨選帝侯之託著手準備制止法國進攻德國的計畫．1672年，他作為一名外交官出使巴黎想遊說法國國王路易十四(Louis XIV，Le Grand)放棄進攻，卻始終未能與法王見面，這次外交活動以失敗而告終．
但是，在1672—1676年留居巴黎期間，萊布尼茨卻開始了自己的學術生涯．當時巴黎是歐洲科學文化中心．他學習了法語，結識了科學界、哲學界的許多著名人士，使他的思想、行動開始越出德國而走向世界．他一生中的許多科學成就和科學思想，如微積分等等，都是在這一時期取得或萌發的．
1673年1月，為了促進英國與荷蘭之間的和解，他前往倫敦進行斡鏇，未果．但他卻趁機與英國學術界知名學者建立了聯繫．他見到了已通信三年的奧頓伯格，結識了R．胡克(Hooke)、R．玻意耳(Boyle)等人．1673年3月回到巴黎，4月即被推薦為英國皇家學會會員．這一時期，他的興趣越來越明顯地朝向數學和自然科學．
1673年2月，他的保護人和摯友馮·舍恩博恩去世，使萊布尼茨失去了職位和薪金，僅僅是一位家庭教師了，當時年僅28歲．他曾多方設法謀求外交官職位或在法國科學院謀職，都沒有成功．因此只好接受漢諾瓦公爵約翰·弗里德里希(Johann Friedrich)的邀請，離開巴黎前往漢諾瓦．
萊布尼茨於1676年10月4日離開巴黎，先在倫敦短暫停留，繼而前往荷蘭見到了A．U．列文虎克(Leeuwenhoek)．列文虎克使用顯微鏡第一次觀察了細菌、原生動物和精子，這些對萊布尼茨的哲學思想曾經產生了影響．他於11月底抵達漢諾瓦，擔任不倫瑞克公爵府法律顧問兼圖書館長．漢諾瓦成了他的永久居住地．
在漢諾瓦定居後，萊布尼茨廣泛地研究哲學和各種科學、技術問題．他的哲學思想逐漸走向成熟，同時也從事多方面的學術文化和社會政治活動．不久他就成為宮庭議員，在社會上開始聲名顯赫，生活也由此而富裕．1682年，與O．門克(Mencke)創辦拉丁文科學雜誌《教師學報》(又譯《學術記事》)(Acta eruditorum lip-siensium，1682—1732)．他的數學、哲學文章大都在該雜誌刊登．
1679年，不倫瑞克公爵約翰·弗里德里希突然去世，其弟奧古斯特(Ernestus Augustus)繼任爵位，萊布尼茨仍保留原職．新公爵夫人蘇菲(C．U．H．Sophie)是他的哲學學說的崇拜者，“世界上沒有兩片完全相同的樹葉”，這一名言就出自他與蘇菲的談話．新公爵聘請他編寫不倫瑞克家族的歷史．為了從事這一工作，他在歐洲作了廣泛的學術旅行．
1687年，萊布尼茨離開漢諾瓦外出旅行．1688年5月抵達維也納，拜見了奧地利皇帝利奧波德一世(Leopold Ⅰ)，他為皇帝構畫出的一系列經濟、科學規劃，給皇帝留下了深刻印象．他試圖在奧地利宮庭中謀一職位，但直到1713年才得到肯定答覆，而他請求奧地利建立一個“世界圖書館”的計畫則始終未能實現．隨後他前往威尼斯，然後抵達羅馬．在羅馬，他被選為羅馬科學與數學科學院成員．1690年3月左右回到漢諾瓦，由於撰寫不倫瑞克史料的功績，他獲取了樞密顧問宮職務．
在1700年世紀轉變時期，萊布尼茨熱心地從事於科學院的籌劃、建設事務．他竭力提倡集中人才研究學術、文化和工程技術，從而更好地安排社會生產，指導國家建設．從1695年起，他就一直為在柏林建立科學院而四處奔波，1698年為此親往柏林．1700年當他第二次訪問柏林時，終於得到了弗里德里希一世(FriedrichⅠ，1701—1713年在位)，特別是其妻子(漢諾瓦奧古斯特公爵之女)的贊助，建立了柏林科學院，他出任首任院長．1700年2月，他被選為法國科學院院士．
1713年初，維也納皇帝授予他帝國顧問的職位，並封他為男爵，邀請他指導建立科學院．俄國的彼得大帝(Peter I， The Great)也在1711—1716年幾次聽取了他關於建立科學院的建議，並於1712年給予他一個有薪水的數學和科學宮庭顧問的職務．1712年左右，他被維也納、不倫瑞克—紐倫堡、柏林、維也納和彼得堡五個王室所雇用．他一有機會總是鼓吹他的編寫百科全書、建立科學院以及利用技術改造社會的計畫．後來維也納科學院、彼得堡科學院先後都建立起來了．傳說他還曾寫信建議康熙皇帝在北京建立科學院．
漢諾瓦公爵奧古斯特選帝侯1698年去世後，繼任的公爵喬治·路德(George Ludwig，1660—1727，即後來的英王喬治一世)對萊布尼茨不甚信任，使他在各個王室包括在漢諾瓦都開始遭受冷遇．
1714年，當聽到喬治·路德成為英國國王的訊息後，68歲高齡的萊布尼茨於9月14日從外地回到了漢諾瓦．但三天前喬治·路德已經作為喬治一世國王前往英國了．他請求在倫敦宮庭謀一歷史學家的職位，卻被喬治一世拒絕．他憂心忡忡，處境每況愈下，晚年悽慘悲涼．1716年夏，喬治一世訪問漢諾瓦時，曾同他一起度假，這給了他少許安慰．1716年11月14日，由於痛風和膽結石症引起腹絞痛臥床一周后，萊布尼茨離開了人世，終年70歲．
數 學
微積分 1666年，萊布尼茨寫成“論組合術”(De ArtCombinatoria)一文，討論了平方數序列
0，1，4，9 16，…
的性質，例如它的第一階差為
1，3，5，7，…，
第二階差則恆等於
2，2，2，…
等．他注意到，自然數列的第二階差消失，平方序列的第三階差消失，等等．同時他還發現，如果原來的序列是從0開始的，那么第一階差之和就是序列的最後一項，如在平方序列中，前5項的第一階差之和為 1＋3＋5 +7=16，即序列的第5項．他用X表示序列中項的次序，用Y表示這一項的值．這些討論為他後來創立微積分奠定了初步思想，可以看作是他微積分思想的萌芽．“論組合術”是他的第一篇數學論文，使他躋身於組合數學研究者之列．
1672年，惠更斯給萊布尼茨出了一道他自己正同別人競賽的題目：求三角級數(1，3，6，10，…)倒數的級數之和
萊布尼茨圓滿地解決了這一問題，他是這樣計算的：
初次成功激發了他進一步深入鑽研數學的興趣．通過惠更斯，他了解到B．卡瓦列里(Cavalieri)、I．巴羅(Barrow)、B．帕斯卡(Pascal)、J．沃利斯(Wallis)的工作．於是，他開始研究求曲線的切線以及求平面曲線所圍圖形的面積、立體圖形體積等問題．1674年，他學習R．笛卡兒(Descartes)幾何學，同時對代數性發生了興趣．這一時期，他檢索了已有的數學文獻．
對於當時數學界密切關注的切線問題和求積問題，萊布尼茨在前人的基礎上提出了一個普遍方法．這個方法的核心是特徵三角形(characteristic triangle)．在帕斯卡、巴羅等人討論過的特徵三角形的基礎上，他建立了由dx，dy和PQ(弦)組成的特徵三角形．其中dx，dy的意義是這樣的：在他1666年“論組合術”中所考慮的序列中，用dx表示相鄰的序數之差，dy表示兩個相鄰項值之差，然後在數列項的順序中插入若干dx，dy，於是過渡到了任意函式的dx，dy．特徵三角形的兩條邊就是任意函式的dx，dy；而PQ 則是“P和 Q之間的曲線，而且是T點的切線的一部分”．如圖1，T是曲線y=f(x)上的一點，dx，dy分別是橫坐標、縱坐標的差值．
利用這個特徵三角形，他很快就意識到兩個問題：
(1)曲線的切線依賴於縱坐標的差值與橫坐標的差值(當這些差值變成無窮小時)之比．通過考慮圖1中△pqr和△STU，發現△PQR∽△STU，從而有dy/dx=Tu/Su．也就是說，曲線y上過T點的切線的斜率是dy/dx．
(2)求積(面積)依賴於橫坐標的無限小區間的縱坐標之和或無限窄矩形之和．
有了這些思想，他很快就推導出了一大批新結論．用他自己的話說就是，從特徵三角形出發，“毫不費力，我確立了無數的定理”．
根據萊布尼茨留下的遺稿可以判定，他是在1673年建立起特徵三角形思想的．他將圖1中特徵三角形的斜邊PQ用“dS”表示，這樣特徵三角形又稱為微分三角形(differential triangle)如圖2，其中 ds2=dx2+dy2．
利用特徵三角形，萊布尼茨早在1673年就通過積分變換，得到了平面曲線的面積公式
這一公式是從幾何圖形中推導出來的，經常被他用來求面積．
1673—1674年，他給出了求一條曲線y=y(x)繞x軸鏇轉一周所形成的鏇轉體的表面積A的公式
同時，他還給出了曲線長度公式
在求面積問題方面，萊布尼茨深受卡瓦列里“線由無窮多個點構成，面由無窮多條線構成”思想的影響，認為曲線下的面積是無窮多的小矩形之和．1675年10月29日，他用“∫”代替了以前的和符號“OMN”(“∫”是Sum 和)的第一個字母“s”的拉長)，用∫ydx表示面積，在這份手稿中，他還從求積出發，得到了分部積分公式
1676年11月，他得出了公式
其中n是整數或分數(n≠-1)．
萊布尼茨的積分方面的工作是與微分方面的工作交叉進行的．
由於研究巴羅的著作，以及引入特徵三角形，萊布尼茨越來越強烈地意識到，微分(主要是導數、求切線)與積分(求和)必定是相反的過程．在1675年10月29日的手稿中，他就注意到，面積被微分時必定給出長度，因此他開始探討“∫”的運算(積分)和“d”的運算(微分)之間的關係，認識到要從y回到dy，必須做出y的微差或者取y的微分．經過這種不充分的討論，他斷定一個事實：作為求和的過程的積分是微分的逆．這樣，萊布尼茨就第一次表達出了求和(積分)與微分之間的關係．
萊布尼茨於1675—1676年給出了微積分基本定理(後來又稱為牛頓-萊布尼茨公式)
(A為曲線f下的圖形的面積，圖3．)
於1693年給出了這個定理的證明．以前，微分和積分作為兩種數學運算、兩類數學問題，是分別地加以研究的．卡瓦列里、巴羅、沃利斯等許多人得到了一系列求面積(積分)、求切線斜率(導數)的重要結果，但這些結果是孤立、不連貫的．雖然他們已開始考慮微分和積分之間的關係，然而只有萊布尼茨和牛頓(各自獨立地)將微分和積分真正溝通起來，明確地找到了兩者的內在的直接聯繫：微分和積分是互逆的兩種運算．而這正是建立微積分學的關鍵所在．只有確立了這一基本關係，才能在此基礎上構建系統的微積分學．並從對各種函式的微分和求積公式中，總結出共同的算法程式，使微積分方法普遍化，發展成用符號表示的微積分運算法則．
萊布尼茨於1684年10月發表在《教師學報》(Acta erudito-rum)上的論文，題目是“一種求極大值與極小值和求切線的新方法，它也適用於無理量，以及這種新方法的奇妙類型的計算”(Nova Methodus pro Maximis et Minimis，itemque tangentibus，quae necfractas，necirrationales quantitates moratur，et singularepro illis Calculi genus)，在數學史上被公認為是最早發表的微積分文獻．
早在1677年7月11日前後及11月左右，萊布尼茨明確定義了dy為函式微分，給出了dy的演算規則：
“如果a是給定的常數，則da=0，dax=adx；
加法和減法 v=z—y＋w＋x，dv=dz-dy+dw＋dx；
乘法 y=vx，dy=vdx+xdv
在1676—1677年的手稿中，他利用特徵三角形分析了曲線切線的變化情況：對於曲線v=v(x)，當dv與dx之比為無窮大時，切線垂直於坐標軸(x軸)．當dv與dx之比等於0時，切線平行於x軸，當dv=dx≠0時，則切線與坐標軸成45°角，他指出，對於曲線v，當dv=0時，“在這個位置的v，明顯地就是極大值(或極小值)”，他詳細討論了當dv＜0，而變成dv=0後又dv＜0時取極大值，反之則取極小值的情形．他還給出了拐點——曲線的凹凸情況發生變法的條件是d2v=0．
以後，萊布尼茨具體求出了各種各樣複雜函式的微商(導數)．1686年，給出了對數函式，指數函式的微商．1695年求出了y=xx的微商dy=xx(1+lnx)，等等．
他引入了n階微分的符號dn，並且給出了高階微分的“萊布尼茨法則”：
其中
n！=1×2×3×…×(n-1)×n．
萊布尼茨在積分方面的成就，後來比較集中地寫在1686年5月發表在《教師學報》上的一篇論文中，題為“潛在的幾何與不可分量和無限的分析”(De Geometria recondita et Analysi Indivisi-bilium atque Infinitorum)．
品中出現了積分符號．同年，他引入了空間曲線的“密切”(osculating)這一術語，並給出了曲率ρ公式：
其中R為曲率半徑．
1692年和1694年，他給出了求一族曲線 f(x，y，α)=0(α為曲線族參數)包絡的普遍方法：在
中消去α．實際上，用微積分方法研究幾何在微積分奠基者(牛頓、萊布尼茨等)那裡已經開始了．切線、包絡等幾何問題在萊布尼茨手中是與微積分連在一起的．
無窮級數 在微積分的早期研究中，有些函式如指數函式等超越函式的處理相當困難，然而人們發現，若用它們的級數來處理，則非常有成效．因此，無窮級數從一開始就是萊布尼茨、牛頓等人微積分工作的一個重要部分．有時使用無窮級數是為了計算一些特殊的量，如萊布尼茨曾用無窮級數表達式計算π(圓周率)．
在求面積的過程中，通過無窮級數表示圓在第一象限的面積，他得到了π的一個十分漂亮的表達式(圖4)：
1673年左右，他獨立地得到了sinx，cosx和arctgx等函式的無窮級數展開式．還得到了圓面積和雙曲線面積的具體展開式，並且將這些展開式與反正切、餘割、正弦函式、自然對數函式、指數函式聯繫起來了．他經常利用級數展開式研究超越函式．有時還將多項式定理用於分式函式或超越函式的展開式．
無窮級數展開式，得到了如下的式子：
誤的．直到1734—1735年，L．歐拉(Euler)才得到
在1713年10月25日寫給約翰·伯努利(John Bernoulli)的信中，萊布
“萊布尼茨判別法”，但他當時的證明卻錯了．在考慮級數還相當混亂．
微分方程 微分方程在微積分創立之初就為人們所關注．1693年，萊布尼茨稱微分方程為特徵三角形的邊(dx，dy)的函式．在微分方程方面，他進行了一系列工作．其中有些工作是十分獨特的．
1691年，他提出了常微分方程的分離變數法，解決了形如
型方程的求解問題．方法是，先寫成
然後兩邊積分．
這一年，他還提出了求解一次齊次方程
的方法：
因此經過這種變換，原來的一次齊次方程就變成了
1694年，他證明了把一階線性常微分方程y′＋P(x)y=Q(x)化成積分方程的正確方法，他的方法使用了因變數替換．同時，他還給出了(y′)2+p(x)y′＋q(x)=0的解法．1694年，他和約翰·伯努利引進了找等交曲線或曲線族的問題，並求出了一些特殊問題的解．
1696年，他證明了，利用變數替換z=y1-n，可以將伯努利方程
變換x=P11u+P12v，y=P21u+P22v可以將微分方程
a00＋a10x＋(a01＋a11x)y′=0
進行簡化．
通過求解微分方程，萊布尼茨解決了許多具體問題．例如，1686年，他解決了這樣的問題：求一條曲線，使得一個擺沿著它作一次完全振動，都用相等的時間，而無論擺所經歷的弧長怎樣(即等時問題)．他指出，
證明，並認識到了圓函式、三角函式的超越性，弄清了許多超越函式的基本性質．此外，他還考慮過機率方程．這一時期，他還求出了十分重要的曳物線方程：
1691年，他給出了自達·芬奇(L．Da Vinci)時代就考慮過的懸鏈線(catenary，這個名稱是萊布尼茨給出的)方程為
1696年，約翰·伯努利提出了著名的最速降線問題：
求從一給定點到不是在它垂直下方的另一點的一條曲線，使得一質點沿這條曲線從給定點P1下滑所用的時間最短(圖5)；其中摩擦和空氣阻力都忽略．
這是約翰·伯努利向全歐洲數學家發出的挑戰．1697年，萊布尼茨和I．牛頓(Newton)、G．F．A．洛比達(L’Hospital)、約翰·伯努利分別解決了最速降線問題，指出這是由方程
表示的上凹的鏇輪線，並由此開始了變分法的研究．
數學符號、代數 萊布尼茨在微積分方面的貢獻突出地表現在他發明了一套適用的符號系統．1675年引入dx表示x的微分，“∫”表示積分，ddv，dddy表示二階、三階微分．1695年左右用dmn表示m階微分．他比別人更早更明確地認識到，好的符號能大大節省思維勞動，運用符號的技巧是數學成功的關鍵之一．他自覺地和格外慎重地引入每一個數學符號，常常對各種符號進行長期的比較研究，然後再選擇他認為最好的、富有啟示性的符號．他創設的符號還有
此外還有對數符號、函式符號、行列式符號等等．很多符號的普遍使用與他的提倡和影響密切相關．他還引入了“函式”(function)、“常量”(constant quantity)、變數”(variate)、“參變數”(para-meter)等術語．
在代數學方面，萊布尼茨不僅強調引入符號的重要性，而且還討論了負數、複數的性質，認為複數的出現是無害的，斷言複數的對數是不存在的，為此曾在當時的數學界掀起了一場關於負數、虛數的對數之爭論．在研究複數時，他還得出過這樣的結論：共軛複數的和是實數
用一般的複數表示．他把虛數看作是存在(being)與非存在(not-being)的中介．
在1678年以前，萊布尼茨就開始了對線性方程組、行列式的研究，對消元法從理論上進行了探討．在1693年4月28日致洛比達的信中他提出了行列式概念：“我引進方程：
此處，在兩個數碼中，前者表示此數所屬的方程式，後者代表此數所屬的字母(未知數)．”這樣，他創設了採用兩個數碼的係數記號，相當於現在的aik，為矩陣和行列式一般理論的發展提供了方便的工具．
萊布尼茨與牛頓的發明權之爭 1698年，瑞士人法蒂奧·德迪勒(Nicolas Fatio de Duiller)斷言，牛頓比萊布尼茨先發明微積分，而後者可能是剽竊，於是掀起了一場發明微積分的優先權問題的論戰．擁護萊布尼茨的歐洲大陸派與擁護牛頓的英國數學家之間開始了長達一個多世紀的爭論．1713年，萊布尼茨發表“微積分的歷史和起源”(Historia et origo Calculi differen-tialis，1713)一文，力圖說明自己成就的獨立性．實際上，牛頓在微積分方面的研究雖然早於萊布尼茨，但萊布尼茨成果的發表則早於牛頓．牛頓在《自然哲學的數學原理》(Philosophiaenaturalis principia mathematica)的第一版(1687年)和第二版(1713年)中都寫道：“十年前在我和最傑出的幾何學家G．W．萊布尼茨的通信中，我表明我已知道確定極大值和極小值的方法、作切線的方法以及類似的方法，但我在交換的信件中隱瞞了這方法，……這位最卓越的人在回信中寫道，他也發現了一種同樣的方法．他並訴述了他的方法，它與我的方法幾乎沒有什麼不同，除了他的措詞和符號而外．”但在第三版(1726年)及以後再版時，這段話卻被刪去了．事實上後來人們都公認，他們是相互獨立地創立了微積分．
儘管如此，他們兩人的工作確有差異，各有特色．牛頓注重物理方面，而萊布尼茨則側重在幾何方面，並與他的“單子”概念有聯繫，有一定的哲學色彩；牛頓的工作方式是經驗的、具體的和謹慎的，在符號方面不甚用心，而萊布尼茨則是富於想像和大膽的，力圖運用符號建立一般法則，善於把具體結果加以推廣和普遍化．
計算機
萊布尼茨是在未看到帕斯卡的加法計算機的情況下，發明他的算術計算機(machina arithmetica)的．1671—1672年，萊布尼茨著手設計、製造計算機——一種能夠進行加、減、乘、除及開方運算的機器．1673年到倫敦旅行時，他隨身攜帶的一個木製計算器的模型引起了人們的極大興趣．人們甚至認為，當時英國皇家學會吸收他為會員，也主要是因為這架計算器，他自己也為這一發明深感自豪．同時這一機器在巴黎也受到人們的熱烈讚揚．
1674年，萊布尼茨在物理學家E．馬略特(Mariotte)的幫助下，製成了一架計算機，並將計算機呈交給巴黎科學院審查驗收，後來還當眾做過演示，他設計的這種新型計算機(圖6)，主要由兩個部分組成：第一部分是固定的，用於加法和減法，其裝置與帕斯卡以前設計的加法機基本一樣；第二部分用於乘法和除法，是他專門設計的乘法器和除法器，由兩排齒輪構成(被乘數輪與乘數輪)，這是萊布尼茨首創的．這架計算機中的許多裝置成為後來的技術標準，那些齒輪被稱為“萊布尼茨輪”．這架機器可進行四則運算．
萊布尼茨充分認識到了計算機的重要性，指出：“這是十分有價值的．把計算交給機器去做，可以使優秀的人才從繁重的計算中解脫出來．”為了製造計算機，他投入大量的精力和財力．當時他曾預言，J．納皮爾(Napier)的計算尺快要閒置不用了．需要代之以能進行各種運算的快速計算機器．雖然他始終未能研製出一種能夠完全自動運算的計算器，但卻概括地描述了今天稱之為程式自動化的思想——計算機發展中的一個重要方面．這也是萊布尼茨的“使所有的推理過程都機械化”宏大計畫中的一部分．
1685年．萊布尼茨敘述了他設計這架能進行四則運算的計算機的經過，用拉丁文寫下了一份手稿，但這篇手稿直到1897年才由C．若爾當(Jordan)公布．刊登在《測量雜誌》(DieZeischift fur Vernessungs-wesen)上．在文末他預言：“我所說的關於該機器的建造和未來的套用在將來一定會更完善，並且，我相信對於將來能見到它的人會看得更清楚．”萊布尼茨早年製作的那些計算機，有一個被幸運地保存下來了，現在存放在漢諾瓦博物館．
二進位制
萊布尼茨發明二進位制的時間，大約是在1672—1676年的巴黎時期．1679年3月15日，萊布尼茨寫了題為“二進位算術”(De I’arthmetique binaire)的論文．文中對二進位制進行了相當充分的討論，與十進位制進行了比較：
給出了將二進位數改寫成十進位制數的法則：
1011000(二進位制)寫成十進位制數就是
26+0+24+23＋0＋0＋0
=64＋16＋8
=88．
下面就是1679年3月15日手稿的一頁(見183頁)．
萊布尼茨不僅完整地解決了二進位制的表示問題，而且給出了正確的二進位制加法與乘法規則．例如，他給出以下這類實例：
1695年5月萊布尼茨與魯道夫·奧古斯特(Rudolphus Au-gustus)大公的一次談話中，大公對他的二進位制非常感興趣，認為一切數都可由0與1創造出來這一點，為基督教《聖經》所講的創世記提供了依據．這是因為唯一完美的上帝是從無到有創造了世界，這與一切數的根源來自0與1的這種體系是對應的．萊布尼茨由此激起熱情，試圖以大公的這一想法來爭取人們對他的二進位制的關注．1697年他在致大公的信函中，就將他創造設計的象徵二進位制的紀念章圖章當作新年禮品奉獻給大公．紀念章正面是大公圖象，背面的設計是這樣的(見圖7)：水面上籠罩著一片黑暗，頂部光芒四射——象徵創世的故事；中間排列著二進位、十進位制數字對照表，兩側是加法與乘法的實例．
萊布尼茨希望能用二進位制證明圓周率π的超越性．
1701年，萊布尼茨將自己的二進制數表給了法國在中國的傳教士白晉(F．J．Bouvet)，同時又將自己關於二進制的論文送交巴黎科學院，但要求暫不發表．同年11月白晉把宋代邵雍(1011—1077)的伏羲六十四卦次序和伏羲六十四方位兩個圖給了萊布尼茨．萊布尼茨對白晉提供的材料欣慰異常，發現中國古老的易圖可以解釋成0—63的二進制數表．萊布尼茨因為從二進制數學理解了六十四卦圖(邵雍的六十四卦方圓圖，圖8)而高興地說：“幾千年來不能很好被理解的奧秘由我理解了，應該讓我加入中國籍吧！”1703年，他將修改補充的論文“關於僅用0與1兩個記號的二進制算術的說明，並附其套用以及據此解釋古代中國伏羲圖的探討”(Explication de l’arthmetique binaire，quise sent des seuls caracteres 0 et 1，avec des remarques Surson utilite，et Sur ce quelle donne Le Sens des aneiennes fi-gures Chinoises Fohy，1703)再送巴黎科學院，要求公開發表．自此二進制公之於眾了．
根據上述歷史事實，表明萊布尼茨並不是受易圖的啟發而發明二進制的，而是他發現了易圖結構可以用二進制數學予以解釋．應該說，萊布尼茨的二進制數學能被用來理解古老的中國文化．自他發現了二者之間的這種關係後，在世界範圍內興起了對易學的數理研究，使人們對易學的興趣日增．
萊布尼茨所進行的計算機設計，程式自動化、程式設計的思想，再加上二進制，為計算機的現代發展奠定了堅實的基礎．
儘管萊布尼茨本人為計算機的設計、二進制的發明感到自豪，但他卻沒有將二進制用於計算機，沒有使二者結合起來．在當時條件下，一個二進位制的機器只會增加技術上的困難，只有隨著電子技術的發展，人們才能將二者有效地結合起來．那種認為他是為計算機而引進二進位制的說法是違背歷史事實的．
邏輯學
萊布尼茨的邏輯學研究包括兩個方面：數理邏輯與形式邏輯．
數理邏輯 萊布尼茨決心構造一門基本學科，這門學科在某些方面象數學，但也包括傳統邏輯中一些尚未發展的研究內容．他注意到了傳統邏輯與數學的共性，發現邏輯及其詞項、命題和三段論與代數中的字母、方程式和變換，具有某種形式上的相似，因此他決心把邏輯表示成一種演算，這種演算研究非數量的抽象關係或形式關係，他曾稱之為普遍數學．他希望建立一種哲學語言(lingua philosophica)或普遍語言(characteristica universalis)，這種語言不僅有助於思想交流，而且有利於思想本身．萊布尼茨力圖發明一種對概念進行演算的理論，使得概念也能象數一樣進行代數演算．
1679年，萊布尼茨開始進行了這方面的研究．他的思想是：每一個簡單的詞項用一個素數表示，每一個合成詞項用素數乘積來表示．如用3表示“能思維的”，7表示動物，人是能思維的動物則可用21表示，寫成21=3.7．一個全稱肯定命題，如果主項的數能被謂項的數整除，則該命題為真．
1686年，萊布尼茨發展了關於概念相等和概念包含的理論，其中引入了詞項a，b，c，…，運算符號—(non，表示“非”)．四個關係
利用這種演算，他成功地將亞里士多德的四種類型的一般命題，表示成了符號公式形式，從而使得用符號表示邏輯命題成為可能．他所考慮的方案和表達方式是：
萊布尼茨認為，有可能構造一種符號系統，這種系統可以作內涵的解釋也可以作外延的解釋．1690年他已經引入了概念的加、減法，用以表示邏輯概念演算及逆運算．他用
表示逆運算，例如A—B=C，若且唯若A=B＋C，且B和C沒有共同的東西．
意義．以此為基礎，他建立了一套全新的理論體系．他的體系要點主要是公式及一套關於詞項、命題的定義與演算規則，如A=B的定義：詞項是同一的或一致的，就是說它們能在任何地方，以一個代之以另外一個而不改變任何命題的真值．A=B表示A和B是同一的．
這種體系在邏輯上是從未有過的，直到約一個世紀以後才由G．布爾(Boole)重新給出．可惜的是，萊布尼茨沒有發展和寫出系統的著作，只留下了大批手稿，其中還有許多是斷簡殘篇，但D．希爾伯特(Hilbert)依然說：“數理邏輯的思想首先是萊布尼茨明顯說出的．”而這種數理邏輯還僅僅只是萊布尼茨符號語言的一部分．
萊布尼茨符號語言的理想是，使一切推理過程、思維過程、爭論過程都像數學一樣能夠計算，甚至能夠交給機器完成．為此，他做了很多工作．
形式邏輯 萊布尼茨在形式邏輯方面的主要工作是，關於判斷的分析理論，在此基礎上的複合概念理論和關於偶然命題的理論，以及“充足理由律”的提出．
他不相信一切論證都可以納入三段論式，因為他了解到條件論證和析取論證不能還原為三段論形式．對於形式證明，他承認經院哲學爭論中使用三段論可能墮落為蠢笨迂腐的學究，但他認為不能沒有形式化，否則就會喪失嚴格性．但對亞里士多德的推崇妨礙了他在這方面取得更大的成就．
區分和研究兩類真理：理性的真理(必然性命題)與事實的真理(偶然性命題)是萊布尼茨整個科學思想體系特別是他的哲學認識論的核心內容．從邏輯方面他又把必然真理分成原始的真理和推理的真理，並且指出：“推理的真理是必然的，它們的反面是不可能的，事實的真理是偶然的，它們的反面是可能的．”他又認為推理是建立在兩大原則上的：(1)矛盾原則，憑著這個原則，我們判定包含矛盾者為假，與假的相對立和相矛盾者為真；(2)充足理由原則，憑著這個原則，任何一件事如果是真實的或實在的，任何一個陳述如果是真的，就必須有一個為什麼這樣而不那樣的充足理由，也許這些理由常常不知道．因此他在邏輯學中引入了“充足理由律”，使之成為與傳統的同一律、矛盾律、排中律相併列的一條基本思維定律．
物理學、力學、光學
1671年，萊布尼茨寫下了《物理學新假說》(Hypothesisphysica noua)，其中包括兩個部分：具體運動原理(Theoriamotus Concreti)，是奉獻給倫敦英國皇家學會的；抽象運動原理(Theoria motus Abstracti)，是奉獻給巴黎科學院的．他的具體原理是試圖從較簡單現象的角度來解釋最重要的複雜現象的一種假說，這種原理建立在以太的相對循環的基礎上，以太則是通過圍繞地球的最初組成狀態的物質才起作用的．他認為物體的全部內聚力依靠構成這些物體的微粒的運動，運動的起因是以太微粒的碰撞，它是物體的全部特性的終極原因．萊布尼茨的抽象原理來源於他對連續體的研究和對運動定律的看法，他認為物質的微粒完全處於靜止狀態時，對一個運動著的物質不存在阻力，只有當微粒構成部分的內在運動時，物體才具有阻力或內聚力．他認為，運動著的物體，不論多么微小，它將帶著處於完全靜止狀態的物體的部分一起運動．
他的物理學研究計畫是：根據一個審慎的計畫和規模，進行某些實驗，藉以在其上建立一個穩定的和論證的物理學堡壘．他的最終的奮鬥目標是為物理學建立一個類似歐氏幾何的公理系統．
萊布尼茨在物理學上最重要的工作是對笛卡兒提出的動量守恆原理進行了認真的探討，提出了能量守恆原理的雛型．
1686年，萊布尼茨在《教師學報》上發表了反對笛卡兒關於力的度量的文章“關於笛卡兒和其他人在自然定律方面的顯著錯誤的簡短證明”(Breuis demonstratio erroris memorabilis Cartesii et aliorum circa Legem naturae)，提出了運動的量的問題，從而開始了與笛卡兒學派關於運動度量的長期爭論，並發展成了力學中的兩個派別．
萊布尼茨指出，如果只用動量(mv，m為物體質量，v為物體運動速度)度量運動，那么“力”(mv2)在自然界不斷增加或減少時，就會導致動量(mv)不守恆，因此他認為動量(mv)不能做為運動的度量單位．
他把力分為“死力”和“活力”，“死力”是靜止物體的“壓力”或“拉力”，這種力是外來的，其度量是物體的質量和物體由靜止狀態到運動狀態時具有的速度的乘積，即動量mv．“活力”(vis viva)是內在於物體的力，是物體的真運動．
在他看來，“活力”應該由物體的質量和該物體所能上升的高度來測量(mh)，按照伽利略落體定律，萊布尼茨成功地計算出高度h與速度v的平方成正比，“活力”保持不變m1v21=m2v22．因此，1695年他正式稱mv2為“活力”(vis viva)，並以mv2作為運動的度量單位，動能的概念就這樣被引入到物理學中來了．這是他在《教師學報》上發表的“動力學實例”(Specimen dynamium)中提出的，這篇論文是萊布尼茨力學的結晶，包含了他的大部分研究成果．萊布尼茨第一次認為“活力”mv2是物理學上的終極因，因而可以轉化為各種各樣的形式，同時還第一次認為mv2的守恆是一個普遍的物理原理，這樣他就有充分的理由證明“永動機是不可能”這樣的觀點．究竟應該以mv2，還是以mv，作為運動的量度，經過長達半個世紀的爭論，直到1743年J．R．達朗貝爾(d’Alembert)指出兩者都是正確的，不過各自所著眼的角度不同罷了，爭論才平息．
萊布尼茨反對牛頓的絕對時空觀，與牛頓的學生S．克拉克(Clarke)進行了長時期的辯論．在萊布尼茨看來，時空與運動、物質是密不可分的，認為“沒有物質也就沒有空間，空間本身不是絕對的實在性”，“空間和物質的區別就象時間和運動的區別一樣．可是這些東西雖有區別，卻是不可分離的”．這些思想後來引起了A．愛因斯坦(Einstein)等人的關注．
在材料力學方面，萊布尼茨支持馬里奧特關於梁受力性質的思想．1684年，他在“固體受力的新分析證明”(Demonstratonsnovae de Resistentia Solidorum)一文中指出，纖維是可以延伸的，它們的拉力與伸長成正比．因此，他提出將胡克定律F=-kx套用於單根纖維，這一假說後來在材料力學中被稱為馬里奧特-萊布尼茨理論．
在光學方面，萊布尼茨利用微積分中的求極值方法，推導出了折射定律：
並嘗試用求極值的方法解釋光學基本定律．
地質學
1693年，萊布尼茨在《教師學報》上發表了一篇論述地球起源的文章，後來擴充為《原始地球》(Protogaea)一書．他認為，地球在早期是一個均勻的、灼熱的熔融球體，形成之後開始逐漸冷卻、收縮．當外表層冷卻到一定程度後，一方面形成了原始的大氣，另一方面形成一種玻璃質和熔窪質所組成的波質地殼，地殼由於收縮而形成褶皺．隨著地球的進一步冷卻，在這些褶皺的地殼上面，周圍的水蒸汽便冷凝成汪洋大海，而由於水蒸汽融解了地殼表面的鹽，因此海水就變鹹了．引起這些地質大變化的原因，有些是地球內部的氣體爆發使地殼破裂，有些是地球表面洪水泛濫所起的作用．前一種原因的作用結果形成火成岩，後一種原因的作用結果產生的是沉積岩層．
萊布尼茨進一步認為，在地殼不斷變化，厚度增加的過程中，地表下形成了大量的氣泡和空穴，當這些氣泡和空穴由於重力等的作用而使其頂部發生坍陷時，地面上的水注入地下洞穴，從而使得原始海洋的水平面降低，因此就出現了山脈，地殼表面上也就有了大陸和海洋之分．同時，地殼表面由於海水的運動就形成了大規模的洪水，洪水對岩石造成了浸蝕，在沖刷、浸蝕的過程中，使得海水越來越鹹，岩石碎片逐漸堆積，形成沉積岩．這種過程在地球的歷史中多次進行，造成了各種沉積岩石和火成岩石互動出現的現象．在每一次大的運動之後，這些作用又達到新的平衡，從而又開始一個新的穩定時期．用這種觀點，萊布尼茨成功地解釋了岩石中含有動物遺蹟以及含有年代不同的岩石碎塊的沉積物這一現象．
對於石煤、合硫物質、石油等易燃物質，萊布尼茨認為火山爆發與地震是形成的原因．對於地層中的生物化石，有些甚至在今天的生物界中還沒有找到與這些化石相應的生物，他認為，這些化石反映了生物的不斷發展，這種現象的最終原因是自然界的變化而非偶然的神跡．
他的地球成因學說，尤其是他的宇宙進化和地球演化的思想啟發了J．B．拉馬克(Lamarck)、C．賴爾(Lyell)等人，促進了19世紀的地質學理論的新進展．
其他領域
萊布尼茨在化學、生物學、氣象學、心理學等領域也做了重要的工作．
在化學方面，1677年，他寫成《磷發現史》(Geschichte derErfindung der phosphois)，對磷元素的性質和提取作了論述，促進了磷元素的發現．他還提出了分離化學製品和使水脫鹽的技術．
在生物學方面，他從哲學角度提出了有機論方面的多種觀點，認為存在介乎動物、植物之間的生物，水螅蟲的發現證明了他的觀點．
在氣象學方面，他曾親自組織人力進行過大氣壓和天氣狀況的觀察．
1696年，萊布尼茨提出了心理學方面的身心平行論(para-llelism)．他強調統覺(apperception)作用，與笛卡兒的互動作用論、B．D．斯賓諾莎(Spinoza)的一元論構成當時心理學三大理論．他還提出了下意識理論的初步思想．
1691年，他還曾致函D．帕潘(Papin)，提出了蒸汽機的基本思想．
1700年前後，他最早提出了無液氣壓機原理，其中完全省掉了液柱．
萊布尼茨一生中，總是希望在學術和政治活動的各個領域都出人頭地，他嘔心瀝血地工作和學習，善於吸收別人的思想，無論何時，只要他抓住一個新課題，就查閱所能找到的與此有關的一切材料，從不囿於傳統的觀念，而是希望產生與他具有的天才相當的創造性作品．為此，他對於要發表的作品總是不厭其煩地反覆推敲．
他善於用訪問和通信的方式與人們討論問題，闡發自己的觀點，一生中曾與千餘人有過書信交往，留下了一萬五千多封信件．與他通信的有各種各樣的人士，既有牛頓、沃利斯、伯努利家族、A．阿爾諾(Arnauld)、N．De馬勒伯朗士(Melebranche)等科學界、哲學界的知名學者，也有歐洲各國的王侯皇妃，距離遠至遠東的中國．信件的內容廣泛，涉及歷史學、哲學、語言學、數學、邏輯學、化學、生物學、物理學、工程技術等等．這些信件記載著他的思想、見解和各種研究成果，有的信件其實就是學術論文．他的許多著作生前未發表，大量的手稿和書信現在還存放在漢諾瓦圖書館中．有許多學者陸陸續續編纂出版過萊布尼茨著作集．第一次世界大戰前，柏林科學院曾計畫編萊布尼茨全集四十卷，這一工作至今仍未能完成．法國科學院則準備在20世紀末編輯出版萊布尼茨全集．
萊布尼茨一生涉獵了各個不同的學術領域，都留下了深深的印記，並且對後世產生了不同程度的影響．他處於文藝復興時期的整體主義和活力論的世界觀與18，19世紀的新原子論和機械論唯物主義的交接時期，他的觀點，對他那個時代來說是激進的，超前的，許多重要思想以後才為人們所接受和重新發現，他的有些工作和觀點無疑還包含著至今尚未認識到的潛力．正如他自己所說的那樣：“我有非常多的思想，假如別人比我更深入透徹地研究這些思想，並把他們心靈的美好創造同我的勞動結合起來，那么，這些思想總有一天會有某些用處的．”
作為哲學家，他在哲學史上與亞里士多德齊名，他的學說與其弟子C．沃爾夫(Wolf)的理論結合，所形成的萊布尼茨-沃爾夫體系極大地影響了德國哲學的發展，尤其是影響了I．康德(Kant)的哲學思想．他開創了德國的自然哲學，以後經過沃爾夫、康德、J．W．V．哥德(Goethe)，到G．W．F．黑格爾(Hegel)得到了長足的進展．萊布尼茨集科學研究與哲學研究於一身，科學思想與哲學思想相互聯繫和相互促進．例如他的單子論與其數學研究中的微分概念是相通的，他的單子概念和有機論自然觀現在仍然受到人們的重視．他與英國哲學家J．洛克(Locke)在認識論方面的創造性的辯論以及他的名著《人類理解新論》(Nouveaux Essais Sur L Entendement Humain)豐富了哲學認識論，同時也加深了歐洲哲學兩大派——經驗主義與理性主義的對峙，而萊布尼茨則被認為是理性主義的重要代表人物之一．V．L．費爾巴哈(Feuerbach)曾經說：“近代哲學領域內繼笛卡兒和斯賓諾莎之後，內容最為豐富的哲學乃是萊布尼茨．”他的邏輯學思想直接推動了20世紀B．羅素(Russell)等人對數理邏輯的研究和發展．
作為一位數學家，萊布尼茨對歐洲大陸數學的發展有著直接的重要的影響，突出地表現在歐洲大陸數學家寧願採用他的d符號(微分符號)而成為“d主義”者，並與英國數學家的“點主義”展開了長達一個多世紀的抗爭，使英國數學由於長期拒絕運用先進的符號和思想而落後於歐洲大陸的數學．直到19世紀英國的C．巴貝吉(Babbage)等青年數學家為改變這種狀況而成立了一個數學分析學會，為反對“點主義”擁護“d主義”而奮鬥，終於採用了萊布尼茨的微分符號．
萊布尼茨建立科學院的思想，直接促進了世界上幾個著名科學院的建立；他的關於所有學科進行綜合研究的觀點，英明地預見了科學發展的趨勢．在他的一生中，關心過各種各樣的科學文化和社會政治問題，鼓吹和平與團結的濟世胸懷貫穿始終，一刻也不懈怠地致力於旨在推動社會進步的學術、文化活動．
可以說，當今在各個學術領域都或多或少地看到他的影響．不過，許多情況是這樣：只有在他的思想重新被發現以後，人們才開始注意到他在這些方面的“優先權”．
萊布尼茨一生沒有結婚，一生沒有在大學當教授．他平時從不進教堂，因此人們送給他一個綽號：Lovenix，即什麼也不信的人．他去世時教士以此為藉口，不予理睬，而宮庭也不過問，無人前來弔唁．彌留之際，陪伴他的只有所信任的大夫和他的秘書J．G．V．艾克哈特(Eckhark)．艾克哈特發出訃告後，巴黎科學院秘書B．L．B．封登納爾(Fontenelle)在科學院例會時向這位外國會員致了悼詞．1793年左右，在漢諾瓦為他建立了紀念碑；1883年，萊比錫的一個教堂附近豎起了他的一座立式個人雕像．1983年，漢諾瓦照原樣重修了被毀於第二次世界大戰中的“萊布尼茨故居”，以供後人瞻仰．
萊布尼茨對中國的科學、文化和哲學思想非常關注．1689年他在羅馬遇見天主教傳教士C．F．格里馬爾迪(Grimaldi，中文教名為閔明我，其時是北京清宮廷的傳教士和數學家)．從格里馬爾迪那裡得知中國的許多情況後，萊布尼茨對中國發生了極大的興趣．他曾交給格里馬爾迪一個希望了解中國情況的提綱，其中開列了30個條目(包括天文、數學、地理、醫學、歷史、哲學、倫理以及火藥、冶金、造紙、紡織、農學等各種技術)．1697年他編輯出版了《中國新事萃編》(Novissima Sinica)一書，內容多為在華傳教士的報告、書信、旅行記略等．在該書的緒論中他寫道：“我們從前誰也不信這世界上還有比我們的倫理更美滿，立身處世之道更進步的民族存在，現在從東方的中國，給我們以一大覺醒！東西雙方比較起來，我覺得在工藝技術上，彼此難分高低；關於思想理論方面，我們雖優於東方一籌，而在實踐哲學方面，實在不能不承認我們相形見絀．”他還強調，中國與歐洲位於世界大陸東西兩端，都是人類偉大燦爛文明的集中地，應該在文化、科學方面互相學習，平等交流．
萊布尼茨很注意蒐集中國的材料，他收藏了關於中國的書籍50多冊．在他的信件中有200多封談到了中國．萊布尼茨可謂是第一位全面認識東方文化尤其是中國文化的西方學者．
萊布尼茨也是受到中國學術界重視的人物．在1859年李善蘭和偉烈亞力(A．Wylie)合譯的《代微積拾級》一書的序言中就說到：“我國康熙時，西國來本之(即萊布尼茨)、奈瑞(即牛頓)創微分、積分二術．”1898年清末黃仲駿所編的《疇人傳》中也列有“來本之”．萊布尼茨的主要哲學著作已陸續翻譯成中文出版．近些年來，中國和歐洲的學術交流，象萊布尼茨曾經期望的那樣，正在日趨興旺．