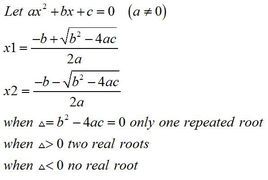方程形式
一般式
一般地，任何一個關於x的一元二次方程經過整理，都能化成如ax+bx+c=0 (a≠0,且a,b,c是常數)的形式。這種形式叫一元二次方程的一般形式。一次項係數b和常數項c可取任意實數，而二次項係數a必須是不等於0的實數。要先確定二次項係數，再確定一次項係數和常數項，必須先把一元二次方程化成一般形式。
變形式
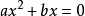一元二次方程（a、b是實數，a≠0）;
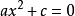一元二次方程（a、c是實數，a≠0）;
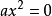一元二次方程（a是實數，a≠0）.
註：a≠0這個條件十分重要.
配方式
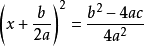一元二次方程兩根式
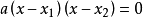一元二次方程求解方法
開平方法
形如x=p或(nx+m)=p(p≥0)的一元二次方程可採用直接開平方法解一元二次方程。
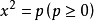一元二次方程如果方程化成 的形式，那么可得 。
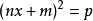一元二次方程如果方程能化成 (p≥0)的形式，那么 ，進而得出方程的根。
注意：
①等號左邊是一個數的平方的形式而等號右邊是一個非負數。
②降次的實質是由一個一元二次方程轉化為兩個一元一次方程。
③方法是根據平方根的意義開平方。
配方法
步驟
將一元二次方程配成(x+m)=n的形式，再利用直接開平方法求解，這種解一元二次方程的方法叫配方法。
用配方法解一元二次方程的步驟：
①把原方程化為一般形式；
②方程兩邊同除以二次項係數，使二次項係數為1，並把常數項移到方程右邊；
③方程兩邊同時加上一次項係數一半的平方；
④把左邊配成一個完全平方式，右邊化為一個常數；
⑤如果右邊是非負數，即可進一步通過直接開平方法求出它的解，如果右邊是一個負數，則判定此方程無實數解。
配方法的理論依據是完全平方公式a²+b²±2ab=（a±b）²
配方法的關鍵是：先將一元二次方程的二次項係數化為1，然後在方程兩邊同時加上一次項係數一半的平方。
舉例
例一：用配方法解方程 3x－4x-2=0
解：將常數項移到方程右邊 3x-4x=2
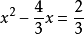一元二次方程將二次項係數化為1：
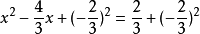一元二次方程方程兩邊都加上一次項係數一半的平方：
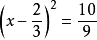一元二次方程配方：
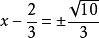一元二次方程直接開平方得：
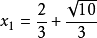一元二次方程∴ , .
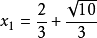一元二次方程∴原方程的解為 , .
求根公式法
步驟
用求根公式解一元二次方程的方法叫做求根公式法。
用求根公式法解一元二次方程的一般步驟為：
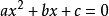一元二次方程①把方程化成一般形式 ，確定a，b，c的值（注意符號）；
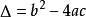一元二次方程②求出判別式 的值，判斷根的情況；
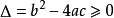一元二次方程③在 （註：此處△讀“德塔”）的前提下，把a、b、c的值代入公式 進行計算，求出方程的根。
推導過程
一元二次方程的求根公式導出過程如下：
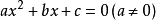一元二次方程
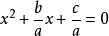一元二次方程
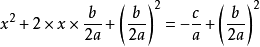一元二次方程（為了配方，兩邊各加 ）
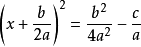一元二次方程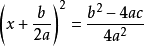一元二次方程
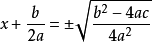一元二次方程
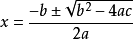一元二次方程（化簡得）。
一元二次方程的求根公式在方程的係數為有理數、實數、複數或是任意數域中適用。
一元二次方程中的判別式:根號下b²－4ac
應該理解為“如果存在的話，兩個自乘後為的數當中任何一個”。在某些數域中，有些數值沒有平方根。
推導過程2
一元二次方程的求根公式導出過程如下：
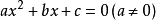一元二次方程
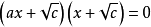一元二次方程
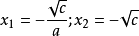一元二次方程
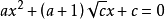一元二次方程
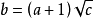一元二次方程
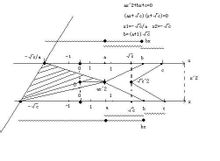一元二次方程a的取值範圍任意，c取值範圍任意，b=(a+1)√c。從a b c 的取值來看可出1億道方程以上，與因式分解相符合。
運用韋達定律驗證：
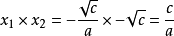一元二次方程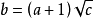一元二次方程
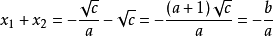一元二次方程因式分解法
因式分解法即利用因式分解求出方程的解的方法。
圖解法因式分解法就是先把方程的右邊化為0，再把左邊通過因式分解化為兩個一次因式的積的形式，那么這兩個因式的值就都有可能為0，這就能得到兩個一元一次方程的解，這樣也就把原方程進行了降次，把解一元二次方程轉化為解一元一次方程的問題（數學化歸思想）。
因式分解法解一元二次方程的一般步驟：
①移項，使方程的右邊化為零；
②將方程的左邊分解為兩個一次因式的乘積；
③令每個因式分別為零，得到兩個一元一次方程；
④解這兩個一元一次方程，它們的解就都是原方程的解。
圖像解法
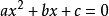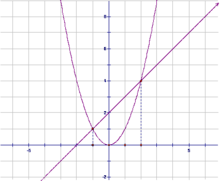
一元二次方程一元二次方程 的根的幾何意義是二次函式 的圖像（為一條拋物線）與x軸交點的X坐標。當 時，則該函式與x軸相交（有兩個交點）；當 時，則該函式與x軸相切（有且僅有一個交點）；當 時則該函式與x軸相離（沒有交點）。
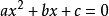一元二次方程另外一種解法是把一元二次方程 化為：
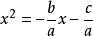一元二次方程的形式。
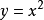一元二次方程則方程的根，就是函式 和 交點的X坐標。
通過作圖，可以得到一元二次方程根的近似值。
計算機法
在使用計算機解一元二次方程時，和人手工計算類似，大部分情況下也是根據下面的公式去解
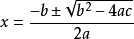一元二次方程可以進行符號運算的程式，比如軟體Mathematica，可以給出根的解析表達式，而大部分程式則只會給出數值解（但亦有部分顯示平方根及虛數）。
根與係數的關係
韋達定理
一元二次方程ax^2+bx+c=0 (a≠0 且△=b^2-4ac≥0)中，設兩個根為x1和x2，則：
x1+x2=-b/a
x1x2=c/a
證明
設x1，x2是一元二次方程ax^2+bx+c=0的兩個解，則有：
a(x-x1)(x-x2)=0
∴ax^2-a(x1+x2)x+ax1x2=0
通過對比係數可得：-a(x1+x2)=b ax1x2=c
∴x1+x2=-b/a x1x2=c/a
計算機解一元二次方程
VB實現方法：
該代碼僅可實現一般形式的求值，並以對話框形式顯示。
dim a,b,c,i
在這裡添加a、b、c的賦值過程。
例如：
a=text1.text
b=text2.text
c=text3.text
if a*2 <> 0 then
i=((0-b)+Sqr(b^2-4*a*c))/2
msgbox i
i=((0-b)-Sqr(b^2-4*a*c))/2
msgbox i
else
msgbox("2a為零")
end if
