弦長公式
公式一
一、引入
直線與圓錐曲線的位置關係是平面解析幾何的重要內容之一,也是聯考的熱點,反覆考查。考查的主要內容包括:直線與圓錐曲線公共點的個數問題;弦的相關問題(弦長問題、中點弦問題、垂直問題、定比分點問題等);對稱問題;最值問題、軌跡問題等。
二 、證明
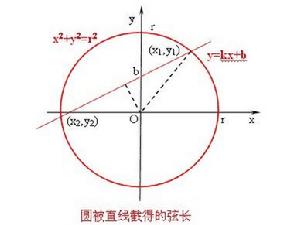
弦長=│x1-x2│√(k^2+1)=│y1-y2│√[(1/k^2)+1]
其中k為直線斜率,(x1,y1),(x2,y2)為直線與曲線的兩交點,"││"為絕對值符號,"√"為根號
證明方法如下:
假設直線為:Y=kx+b
 弦長公式
弦長公式圓的方程為:(x-a)^2+(y-u)^2=r^2
假設相交弦為AB,點A為(x1.y1)點B為(X2.Y2)
則有AB=√(x1-x2)^2+(y1-y2)^2
把y1=kx1+b.
y2=kx2+b分別帶入,則有:
AB=√(x1-x2)^2+(kx1-kx2)^2
=√(x1-x2)^2+k^2(x1-x2)^2
=√1+k^2*│x1-x2│
證明AB=│y1-y2│√[(1/k^2)+1]
的方法也是一樣的
證明方法二
d=√(x1-x2}^2+(y1-y2)^2
這是兩點間距離公式
因為直線
y=kx+b
將其帶入所以y1-y2=kx1+b-(kx2+b)=k(x1-x2)
d=√(x1-x2)^2+(y1-y2)^2
得到
d=√(x1-x2)^2+[k(x1-x2)]^2
=√(1+k^2)(x1-x2)^2
=√(1+k^2)*√(x1-x2)^2
=√(1+k^2)*√(x1+x2)^2-4x1x2
公式二
 弦長公式
弦長公式拋物線
y2=2px,過焦點直線交拋物線於A(x1,y1)和B(x2,y2)兩點,則AB弦長:d=p+x1+x2y
x2=2py,過焦點直線交拋物線於A﹙x1,y1﹚和B﹙x2,y2﹚兩點,則AB弦長:d=p+y1+y22=-2px,過焦點直線交拋物線於A﹙x1,y1﹚和B﹙x2,y2﹚兩點,則AB弦長:d=p-﹙x1+x2﹚
x2=-2py,過焦點直線交拋物線於A﹙x1,y1﹚和B﹙x2,y2﹚兩點,則AB弦長:d=p-﹙y1+y2﹚
公式三
d = √(1+k^2)|x1-x2| = √(1+k^2)[(x1+x2)^2 - 4x1x2] = √(1+1/k^2)|y1-y2| = √(1+1/k^2)[(y1+y2)^2 - 4y1y2]
 弦長公式
弦長公式關於直線與圓錐曲線相交求弦長,通用方法是將直線y=kx+b代入曲線方程,化為關於x(或關於y)的一元二次方程,設出交點坐標,利用韋達定理及弦長公式√(1+k^2)[(x1+x2)^2 - 4x1x2]求出弦長,這種整體代換,設而不求的思想方法對於求直線與曲線相交弦長是十分有效的,然而對於過焦點的圓錐曲線弦長求解利用這種方法相比較而言有點繁瑣,利用圓錐曲線定義及有關定理導出各種曲線的焦點弦長公式就更為簡捷。
d =√[(1+k^2)△/a^2] =√(1+k^2)√(△)/|a|
在知道圓和直線方程求弦長時,可利用方法二,將直線方程代入圓方程,消去一未知數,得到一個一元二次方程,其中△為一元二次方程中的 b^2:-4ac ,a為二次項係數。
補遺:公式2符合橢圓等圓錐曲線 不光是圓。公式/|a|是在整個平方根運算後再進行的……(先開平方瞭然後再除)
2式可以由1推出,很簡單,由韋達定理,x1+x2=-b/a x1x2=c/a 帶入再通分即可。
在知道圓和直線方程求弦長時也可以用勾股定理(點到直線距離、半徑、半弦)。

