方程求根方法
切線法又稱為牛頓法,是一種一般情況下具有二階收斂速度的非線性方程的數值解法。
具體方法如下:
 切線法
切線法 切線法
切線法 切線法
切線法 切線法
切線法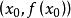 切線法
切線法 切線法
切線法設 是方程 的根,又 為 附近的一個值,過 做 的切線,則切線方程為:
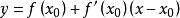 切線法
切線法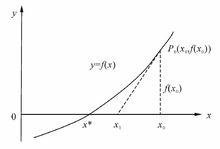 切線法
切線法 切線法
切線法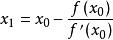 切線法
切線法上述切線與 軸的交點為:
 切線法
切線法 切線法
切線法 切線法
切線法 切線法
切線法如果曲線在 鄰域保持凹凸性不變,從圖中不難看出, 比 更接近方程的真實值 ,由此可以得到一個疊代公式:
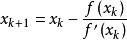 切線法
切線法上面的疊代公式就是切線法的公式,不難看出這個公式實際就是牛頓公式。
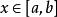 切線法
切線法 切線法
切線法 切線法
切線法可以證明,當 ,且滿足以下條件時,由以上遞推式產生的序列最後收斂到 在 上的唯一實根:
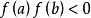 切線法
切線法(1)
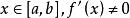 切線法
切線法(2) ;
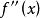 切線法
切線法 切線法
切線法(3) 在 上恆正;
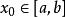 切線法
切線法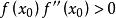 切線法
切線法(4) 初值 應滿足。
收斂性的證明
下面給出牛頓切線法疊代格式收斂的充分條件,為了配合插圖,將充分條件具體表述為:
 切線法
切線法 切線法
切線法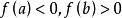 切線法
切線法若(1)函式 在 上連續,且 ;
 切線法
切線法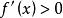 切線法
切線法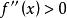 切線法
切線法(2)在區間 上, , 。
 切線法
切線法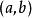 切線法
切線法 切線法
切線法則(1)方程 在區間 上存在唯一的實數根 ;
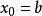 切線法
切線法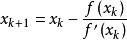 切線法
切線法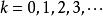 切線法
切線法 切線法
切線法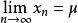 切線法
切線法(2)取初值 ,由疊代公式 ( )定義的數列 一定收斂,且 。
 切線法
切線法 切線法
切線法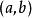 切線法
切線法證明(1)根據連續函式的 介值定理,可得方程 在區間 上解的 存在性;又根據函式的單調性可知方程在區間 的上解具有唯一性。
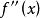 切線法
切線法 切線法
切線法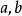 切線法
切線法(2)因為 在 上恆正。利用一階泰勒公式在區間[ )上恆有:
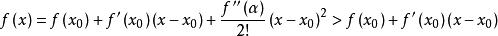 切線法
切線法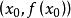 切線法
切線法 切線法
切線法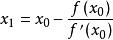 切線法
切線法 切線法
切線法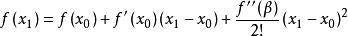 切線法
切線法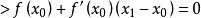 切線法
切線法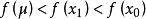 切線法
切線法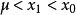 切線法
切線法即曲線在過 點的切線的上方,所以切線與 軸的交點 必滿足 ,又因為即,根據單調性可知 。
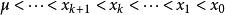 切線法
切線法 切線法
切線法 切線法
切線法利用數學歸納法可以證明 ,即 單調有界數列,所以必收斂。設其極限為 。
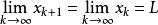 切線法
切線法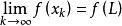 切線法
切線法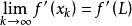 切線法
切線法則 ,根據函式及導數的連續性可知 , 。
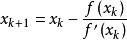 切線法
切線法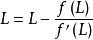 切線法
切線法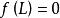 切線法
切線法在疊代式 兩邊同求極限,可得 。從而可得 。
 切線法
切線法 切線法
切線法 切線法
切線法 切線法
切線法根據方程根的唯一性,可以斷定 就是方程 在區間 上存在唯一的實數根 。
計算實例
求方程實根
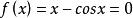 切線法
切線法求方程 的實根。
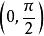 切線法
切線法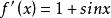 切線法
切線法由零點定理知原方程在 內有實根,
那么疊代公式為:
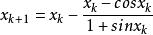 切線法
切線法取初始值 ,疊代序列如下:
| x | 1 |
| x | 0.75036386784024 |
| x | 0.73911289091136 |
| x | 0.73908513338528 |
| x | 0.73908513321516 |
| x | 0.73908513321516 |
由此得到方程的實根為x=0.73908513321516...
上例的c語言程式代碼為:
任意數開n次方
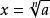 切線法
切線法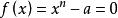 切線法
切線法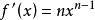 切線法
切線法設 ,那么 ,
從而疊代公式為:
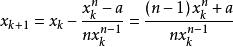 切線法
切線法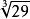 切線法
切線法舉個例子:求
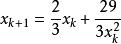 切線法
切線法對應的疊代公式為:
取初值x=2,疊代如下:
| x | 2 |
| x | 3.75000000000000 |
| x | 3.18740740740741 |
| x | 3.07642248706644 |
| x | 3.07232230248782 |
| x | 3.07231682569561 |
| x | 3.07231682568585 |
| x | 3.07231682568585 |
從上面可以看出,只要疊代6次即可求出15位精度的近似值。
任意實數開n次方的c語言代碼為:
文學中的表現
清代小說《蕩寇志》中,出現了劉慧娘用切線法算仰角的情節。
股票術語
切線法是按一定方法和原則在由股票價格的數據所繪製的圖表中畫出一些直線,然後根據這些直線的情況推測股票價格的未來趨勢,這些直線就叫切線。切線的作用主要是起支撐和壓力的作用。支撐線和壓力線的往後的延伸亦對價格的趨勢起一定的制約作用。一般說來,股票價格在從下向上抬升的過程中,一觸壓力線,甚至遠未觸及到壓力線,就會調頭向下。同樣,股票價格在從上向下跌落的過程中,在支撐線附近就會轉頭向上。另外,如果觸及切線後沒有轉向,而是繼續向上或向下,這就叫突破。突破之後,這條切線仍然有實際作用,只是名稱變了。原來的支撐線變成壓力線,原來的壓力線變成支撐線。切線法分析股市主要是依據切線的這個特性。
切線的畫法是最為重要的,畫得好壞直接影響預測的結果。畫切線的方法有很多種,它們都是人類長期研究之後保留下來的精華。著名的有趨勢線、通道線等,此外還有黃金分割線、甘氏線、角度線等。在實際套用中,人們從這些線上獲益不少。
切線法所依據的理論便稱為切線理論。