一.概述
我們把立體幾何學的異面直線所成的角、直線與平面所成的角、平面與平面所成的角,統稱為空間角度。
二.異面直線所成角
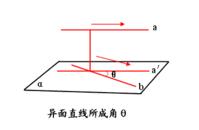
1.定義過空間一點,作分別平行於兩條異面直線的相交直線所成的銳角或
直角,叫異面直線所成角。
異面直線所成角的範圍是(0,π/2].
3.求法(1)定義法
也叫平移法。按照異面直線所成角的定義,平移一條直線或平移兩條直線。轉化成相交直線所成角來求。然後,解三角形求角。
(2)向量法
轉化成兩異面直線的方向向量的夾角或其補角。即用夾角公式
三. 直線與平面所成的角
當直線是平面的斜線(相交但不垂直)時,斜線與其在平面的射影的夾角,叫直線與平面所成的角。
規定:當直線在平面內或直線與平面平行時,直線與平面所成角為0°;當直線與平面垂直時,直線與平面所成角為90°.
直線與平面所成角的範圍是[0,π/2].
3.求法(1)定義法
按照直線與平面所成角的定義。一般通過面的垂線,確定斜線射影。轉化成斜線與射影的夾角。然後,解三角形求角。
(2)法向量法
1°轉化成平面的法向量,與斜線的方向向量所成角的餘角,或補角的餘角。即用公式
sin<向量n,向量b>=|n·b|/|n||b|.
2°轉化成斜線的方向向量, 與斜線射影方向向量所成角,或補角。即用公式
cos<向量a,向量a′>=(a·a′)/|a|| a′|.
四. 平面與平面所成的角
平面與平面所成的角,是用二面角來描述的。
(1)一條直線把平面分成兩部分,每部分叫半平面。
(2)從一條直線出發的兩個半平面組成的圖形叫二面角。
這條直線叫二面角的棱,兩個半平面叫二面角的面。
(3)垂直於棱的平面,與二面角的兩個面相交,得兩條射線,這兩條射線所成的角,叫二面角的平面角。
(4)二面角的度量
二面角的大小,用平面角來度量。平面角為55°,則稱二面角為55°。反之亦然。
(5)平面與平面所成的角
如果把二面角的兩個面延展成兩個平面,那么兩個平面相交的惟一的交線就是二面角的棱。這時二面角的平面角或其補角的大小,是平面與平面所成的角的大小。
二面角的範圍是[0,π]。
3.求法(1)三垂線法
用三垂線定理或逆定理,得兩條垂直於棱的直線。從而得平面角。然後解三角形求角。
此法使用頻率最高。
(2)垂面法
也叫定義法。在棱上選一特殊點,過這點作棱的垂面,得平面角。然後解三角形求角。 (3)垂線法
在棱上選一特殊點,過這點在兩個面內分別作棱的垂線,得平面角。然後解三角形求角。當棱為兩個等腰三角形公共邊時,如求正稜錐側面與底面所成角時,常用此法。
(4)射影面積法
設平面角為θ,則cosθ=S′/S
(5)向量法
轉化成二面角的兩個面的法向量所成角或其補角。即用公式
cos<向量n1,向量n2>=(n1·n2)/|n1||n2|.
五.幾點說明
1.空間角的定義體現了空間問題平面化的數學思想。把空間的角轉化為相交直線(如異面直線所成角、直線與平面所成角)或兩條射線(如二面角的平面角)所成角。
2.空間角的概念,是立體幾何計算題的證明要點。當用傳統的演繹推理法求上述角時,必須詳盡寫明所作的輔助直線、輔助平面;必須按照空間角的定義進行證明。然後計算。然而,用解析法和向量法沒有上述要求。
3. 空間的角包括平面幾何的相交直線所成的角、平行直線所成的角。