射影面積法

射影面積法是運用二面角的平面角來進行射影面積計算的一種面積計算方法。

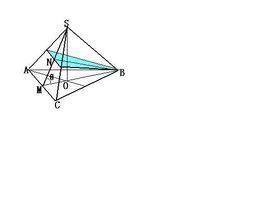
定律定義

已知平面b內一個多邊形的面積為S1，它在平面a內的射影圖形的面積為S2，平面a和平面b所成的二面角的大小為X，則cosX=S2/S1。

推導過程

在兩平面間二面角的求法中，一種是利用餘弦定理，另外一種便是射影面積法。

使用前證明二面角的餘弦等於兩個三角形面積的比。

一個面上取個三角形面積為S1；

在另一個面上做或者找到那個三角形的射影（即以3個點的射影為頂點的三角形）的面積S2；

二面角為X；

則cosX=S2/S1。

適用範圍

海倫公式是用來求三角形面積的公式S=√p(p-a)(p-b)(p-c),其中a，b，c是三角形三邊,p是三角形周長的一半。

這個公式在處理三角形面積尤其是當邊長不是整數時,運算量是相當大的,因此還是推薦使用餘弦定理或正弦定理來解決三角形的面積。

而證明的時候還是要先找到二面角的平面角,因此這種方法不推薦在批卷十分嚴格的高考中使用,不過如果實在找不到平面角,那也只好直接用這個方法了,不過在高考中沒有證明而直接使用此方法會被扣去3~5分。