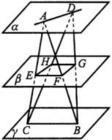
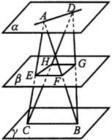
 異面直線
異面直線定義
不同在任何一個平面內的兩條直線叫做異面直線。
 1
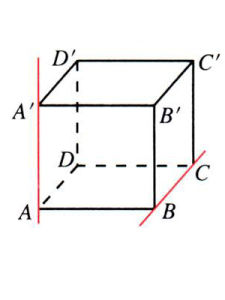
1特點
既不平行,也不相交。
 1
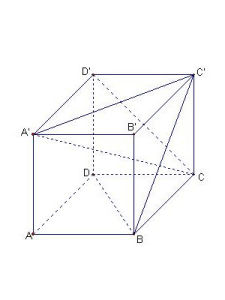
1判定方法
(1)定義法:由定義判定兩直線永遠不可能在同一平面內
(2)定理:過平面外一點與平面內一點的直線,和平面內不經過該點的直線是異面直線。
兩條異面直線所成的角的定義:直線a,b是異面直線,經過空間一點O,分別引直線A//a,B//b,相交直線A,B所成的銳角(或直角)叫做異面直線a,b所成的角。
兩條異面直線垂直的定義:如果兩條異面直線所成的角是直角,則稱這兩條異面直線互相垂直。
兩條異面直線的公垂線的定義:和兩條異面直線都垂直相交的直線叫做兩條異面直線的公垂線。
兩條異面直線的距離的定義:兩條異面直線的公垂線在這兩條異面直線間的線段,叫做這兩條異面直線的公垂線段;公垂線段的長度,叫做兩條異面直線的距離。