定理
線面垂直證明
已知:如圖,PO在α上的射影OA垂直於a。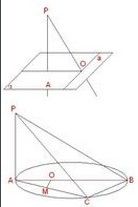 三垂線證明
三垂線證明三垂線定理的證明
。求證:OP⊥a
證明:過P做PA垂直於α
∵PA⊥α且a⊆α
∴a⊥PA
又a⊥OA
OA∩PA=A
∴a⊥平面POA
∴a⊥OP
用向量證明
1.已知:PO,PA分別是平面α的垂線,斜線,OA是PA在α內的射影,向量b包含於α,且向量b垂直於OA,求證:向量b垂直於PA。證明:∵PO垂直於α,∴PO垂直於b,又∵OA垂直b,向量PA=(向量PO+向量OA)
∴向量PA·向量b=(向量PO+向量OA)·向量b=(向量PO·向量b)+(向量OA·向量b)=0,∴PA⊥向量b。
2.已知三個平面OAB,OBC,OAC相交於一點O,∠AOB=∠BOC=∠COA=60度,求交線OA與平面OBC所成的角。
解:∵向量OA=(向量OB+向量AB),O是內心,又∵AB=BC=CA,∴OA與平面OBC所成的角是30°。
三餘弦定理
三餘弦定理:平面內的一條直線與該平面的一條斜線所成角的餘弦值,等於斜線與平面所成角的餘弦值乘以斜線在平面上的射影與該直線所成角的餘弦值。例如:OP是平面OAB的一條斜線,且OP在面上的射影是OC。若∠POC=α(斜線與平面所成角),AB與OC所成角為β(射影與直線所成角),OP與AB所成角為γ(直線與斜線所成角),則cosγ=cosαcosβ
顯然,三垂線定理就是當β=90°的情況。直線垂直射影有cosβ=0,因此cosγ=0,即直線與斜線也垂直。
使用
1、三垂線定理描述的是PO(斜線),AO(射影),a(直線)之間的垂直關係。2、a與PO可以相交,也可以異面。
3、三垂線定理的實質是空間內的一條斜線和平面內的一條直線垂直的判定定理。關於三垂線定理的套用,關鍵是找出平面(基準面)的垂線。至於射影則是由垂足,斜足來確定的,因而是第二位的。從三垂線定理的證明得到證明a⊥b的一個程式:一垂,二射,三證.即第一,找平面(基準面)及平面垂線第二,找射影線,這時a,b便成平面上的一條直線與一條斜線.第三,證明射影線與直線a垂直,從而得出a與b垂直。
註:
1、定理中四條線均針對同一平面而言
2、套用定理關鍵是找"基準面"這個參照系
附:江蘇省《教學要求》中規定自2011年高考起“三垂線定理”不能作為推理論證的依據,要證明。
黑龍江省《教學要求》中規定自2012年高考起“三垂線定理”不能作為推理論證的依據,要證明。
用途
在做圖中,做二面角的平面角。在證明中,證明線線垂直。
在計算中,用歸納法歸攏已知條件,便於計算。

