歷史沿革
 十進制
十進制另有學者對中國青海樂都縣柳灣出土一千多枚新石器時代骨片進行研究,發現它們分屬馬廠、半山、齊家和辛店四個中文化型。骨片長度為2-2.4厘米,厚約1毫米。骨片上有刻痕,少的一個,多不超過八個,每個骨片上的刻痕數目不超過十個,他們以此認為新石器時代已有加法運算和十進制。
另有學者認為,甲骨文中一橫代表1,兩橫相疊代表二,三橫代表三,四橫代表四,X 代表五,“人”形代表六,“十”代表七,“)(”代表八, “九”已經是九;| 代表十,||代表20,|||代表三十,||||代表四十;此外50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000,2000,……9000,10000……40000 都有不同的符號。商代甲骨文“已形成完整的十進制系統”。
北京的中國歷史博物館藏有一把安陽殷墟出土的象牙尺,長15.78厘米,分為十寸,說明中國商代的十進制幾經用在長度上了。
中國周代金文的紀數法,繼承商代的十進制, 又有明顯的進步,十進數量級符號有十、百、千、萬、億,如西周金文“伐鬼方……俘萬三千八十一人”,“武王遂征四方,俘人三億萬有二百三十”,出現了位值記數,例如 “俘牛三百五十五“,其中三百五十五寫成“三全XX”,前面的“全”是金文的“百”,後面兩個XX是五十五,省去了“十”,出現了位置概念,但尚未形成完整的位值制。金文商鞅量銘還出現分數。
春秋戰國時代,出現嚴格的十進位制籌算記數,以空代表0,也發明了用於十進位制乘法、除法的九九表<
公元前3400年左右,古埃及有基於十進制的記數法。但這種十進制並無位值的概念。
吠陀時代前800年的印度儀軌經類文獻中的繩法經中包含大量分數的套用,但並無證據顯示此時的文字記數系統是十進制的。
公元前500年,希臘古典時期的阿提卡數字為十進制系統。
公元前300年,印度的婆羅迷數字為十進制。婆羅迷十進制毫無位值概念。
出土於巴基斯坦的古印度巴克沙利手稿可能是世界上最早的包括0的“真正的”十進制系統,但它的具體時間有爭議。
起源
一般“共識”認為現在世界通行的十進制起源於印度。從20世紀初,國際上許多學者,包括李約瑟在內對印度起源論提出了質疑。
早在1907年印度學者Kaye指出“我研究的目的,在於指出我們關於現代數學記數的基礎很不牢固,值得重新研究。從印度文字,碑文證據,早期印度日的記數法,以及現代印度土著的風俗習慣等方面,指明現代記數可能來自外國
印度學者Datta and Singh認為,“印度不存在記述這些數字及其基本算術運算方法的早期文獻,發明人不可知”
德國學者Menninger 認為印度十進制的起源,模糊不清。
李約瑟指出,古印度的數字系統,用單獨的符號表示10和10的倍數,相對於希臘或希伯來數字系統,毫無進步……印度數字中的0,很可能起源於東印度和中國南方文化接壤的地區。印度是否採納中國算籌的空檔而受啟發?關鍵在於中國在比孫子算經早很多的時期,已經擁有十進位值制。
曾任國小教師的法國通俗作家Ifrah斷言,458年的印度耆那教文獻Lokavibhaga中的 panchabhyah khalu shunyebhyah param dve sapta chambaram ekam trini cha rupam cha代表“五空和二和七和天,一和三和形,就是13107200000”,“是世界上最早的帶零的十進位數字”。他還說,印度的零、一、二、……九的詞多了,有eka,pitamaha,adi,tanu……都指“一”,dvi,ashvin,Yama, yamala, netra,bahu,guophau, paksha 都可以是“二”……。有學者認為現在世界各國使用的阿拉伯數字都起源於這一系統。
美國學者Robert Temple根據李約瑟《中國科學技術史》縮寫的“Genius of China”,認為今日世界通行的十進制,真正起源地在中國。
新加坡著名數學史家蘭麗蓉認為阿拉伯數字的基本概念,不可能起源於印度婆羅迷數字,而是起源於中國籌算。籌算用九個符號代表一切數,其加法減法,天然包含在算籌之中,三減三就是從算版上取去三個算籌,算版上自然而然留下一個空位,這就是零,籌算中稱為‘空’。無獨有偶,印度在沒有發明‘0’這個符號之前,和中國的籌算一摸一樣,也用一格空檔來表示零,稱為“sunya”!,這就沒有天然的理由了;而“983 542”到底是一個數字還是兩個數值,容易產生混淆,後來印度才用“.”或“0”代表sunya。此外印度的加減乘除運算程式,上、中、下三行排列的方式,除數和被除數首位對齊,留籌算式的空白(!)而非“0”,從左往右計算的規則,商數右邊留空白而沒有補“0”,每算一步之後,除數右移一位,甚至餘數表示為分數的上、中、下三行表示方法,居然和孫子算經中敘述的孫子除法雷同,這三點是印度十進位數字系統的基礎概念全盤來自籌算的鐵證。
現存最古老的運用印度數字的算術著作:10世紀波斯數學家伊本·拉班在所著《印度算術原理》中詳細敘述的印度除法,印度開平方術,開立方術也同樣源自孫子算經。
0……9符號來自印度,但背後的十進位制概念,則來自籌算。將空寫成0,只是書寫方式,沒有概念上的發明。至於中國籌算十進制如可傳入印度,蘭麗蓉認為中國古時官員,商人僧侶和旅行家,腰掛算籌袋很平常,而中國和印度來往密切,傳入印度不難理解。事實上早於458年一個半世紀,從公元266-399年間,就有竺法護,康法郎,於法藍,竺佛念,慧常,進行,慧辯,支法領,法淨等高僧到過印度了,此後還有著名的法顯到過佛國。
淵源
首先,現在人們日常生活中所不可或離的十進位值制,就是中國的一大發明。至遲在商代時,中國已採用了十進位值制。從現已發現的商代陶文和甲骨文中,可以看到當時已能夠用一、二、三、四、五、六、七、八、九、十、百、千、萬等十三個數字,記十萬以內的任何自然數。這些記數文字的形狀,在後世雖有所變化而成為現在的寫法,但記數方法卻從沒有中斷,一直被沿襲,並日趨完善。十進位值制的記數法是古代世界中最先進、科學的記數法,對世界科學和文化的發展有著不可估量的作用。正如李約瑟所說的:“如果沒有這種十進位制,就不可能出現我們現在這個統一化的世界了。”
大地灣仰韶晚期房F901中曾出土一組陶質量具,主要有泥質槽狀條形盤、夾細砂長柄麻花耳鏟形抄、泥質單環耳箕形抄、泥質帶蓋四把深腹罐等。其中條形盤的容積約為264.3立方厘米;鏟形抄的自然盛穀物容積約為2650.7立方厘米;箕形抄的自然盛穀物容積約為5288.4立方厘米;四把深腹罐的容積約為26082.1立方厘米。由此可以看出,除箕形抄是鏟形抄的二倍外,其餘三件的關係都是以十倍的遞增之數。這些度量衡具的發現也為研究我國古代十進制的起源等,提供了非常珍貴的實物資料。
古巴比侖的記數法雖有位值制的意義,但它採用的是六十進位的,計算非常繁瑣。古埃及的數字從一到十隻有兩個數字元號,從一百到一千萬有四個數字元號,而且這些符號都是象形的,如用一隻鳥表示十萬。古希臘由於幾何發達,因而輕視計算,記數方法落後,是用全部希臘字母來表示一到一萬的數字,字母不夠就用加符號“‘”等的方法來補充。古羅馬採用的是累積法,如用ccc表示300。印度古代既有用字母表示,又有用累積法,到公元七世紀時方採用十進位值制,很可能受到中國的影響。現通用的印度——阿拉伯數碼和記數法,大約在十世紀時才傳到歐洲。
在計算數學方面,中國大約在商周時期已經有了四則運算,到春秋戰國時期整數和分數的四則運算已相當完備。其中,出現於春秋時期的正整數乘法歌訣“九九歌”,堪稱是先進的十進位記數法與簡明的中國語言文字相結合之結晶,這是任何其它記數法和語言文字所無法產生的。從此,“九九歌”成為數學的普及和發展最基本的基礎之一,一直延續至今。其變化只是古代的“九九歌”從“九九八十一”開始,到“二二如四”止,而現在是由“一一如一”到“九九八十一”。
印度與阿拉伯的十進位制
七世紀之前,印度數字用一到九個符號,以空代零。時至今日,南印度泰米爾納德邦仍通行九個符號加空代零,另有十、百、千符號。
公元七世紀,印度Nagari數字出現0。
公元八世紀唐朝太史監印度人瞿曇悉達在開元年間主持編纂的《開元占經》卷104將印度數字“·”(零)引入中國,“右天竺算法用上件九個字乘除,其字皆一舉扎而成,凡數至十進入前位,每空位處恆安一點”,但只有文字敘述,未曾畫出印度數嗎的形狀。
學界公認,印度帶“0”的十進位制最早出現在876年印度瓜廖爾Bhojadera碑文,“933”年印度歷(公元876年)碑文文記述一塊“270” 乘 “187” 的花園,每日給廟奉獻“50”個花圈。“933”、“270”、“187”、“50”四個印度數字,已經是現代阿拉伯數字了。
印度本土用印度數字的算術著作已蕩然無存,但保留在多種阿拉伯文著作中。存世最古老的一本用印度數字的算術書,當推十世紀波斯數學家伊本·拉班所著的《印度算術原理》,他在該書第一章詳細敘述印度十進位制數字的原理。他寫道“必須認識九個數字۹۸۷۶۵۴۳۲۱,第一個是一,第二個是二,一直到九,並且頭一個是個位,第二個是十位,第三百位,第四千位,第五萬……十之後必須加一個零,一百之後必須加兩個零,即記十為10,百為100。
九世紀花拉子米,十世紀伊本·拉班,十一世紀烏克里迪西等阿拉伯數學家都著有關於印度算術的著作,所述的加、減、乘、除、開平方、開立方的程式,從排列方式,留空方式,數字位移方式,以至餘數、分數的表示格式,都和中國公元一世紀的九章算術、5世紀孫子算經所述的相應算術運算相同。中世紀的印度-阿拉伯數學家用沙盤進行計算。沙盤可以是帶沙子的地面或一塊木板,上鋪一層薄沙,劃上格子,用手指頭或一根棍將阿拉伯數字劃在格子裡面。因為有格子,所以空格就代表零,不必寫“0”,這和中國籌算以空代零的習慣一樣。
印度文數字的0,1,2……9中的“0”,是印度數學對十進位制的重要貢獻,它克服了算籌數碼空檔的缺點,例如可以指6,600,60000……使十進位制草算在中世紀阿拉伯國家大為流行。
中國南宋數學家秦九韶在算籌碼中引入圓圈可能受到印度“0”的影響。
中國與十進制
中國古代使用的是十進制計數法,即每滿10個數目就進一個單位,如10個1進為10,10個10進為100等。十進制起源於何時已不可考,但至遲春秋時期,中國古人就已經能夠熟練使用十進制進行計數和運算了。
中國古代的十進制計數方法實際包括了“十進制”和“位值制”兩種計數方法。位值制就是以位置定數目,如22,同樣是兩個2,第一個2因位於十位上,故代表20,第二個2因位於個位上,故代表2。可以看出,由於使用了位值制,就可以很簡捷地記錄較大的數目。
中國是世界上第一個同時使用“十進制”和“位值制”的國家。古埃及、古希臘和古羅馬都沒有發明位值制。古代美洲瑪雅人和兩河流域的古巴比倫人雖然發明了位值制,卻分別使用的是二十進制和六十進制計數法。
今天通用的十進制阿拉伯數字系統,實際上是10世紀後由印度傳入地中海沿岸及西歐各國。 考證歷史,直到6世紀末以後,印度才開始使用十進制計數法。於是,有學者認為,印度的十進制計數法可能源自中國,古代中國才是今天通行的十進制計數法的真正源頭。
歷史沿革
有學者認為,北京周口店的一萬多年前的山頂洞人遺址出土的骨管,以一個圓點代表1,兩個圓點並列代表2,三個圓點並列代表3,五個圓點上二下三排列代表5,長圓形可能代表十。中國著名數學史家,國際科學史研究院通訊院士李迪教授認為山頂洞人骨管符號是“一種十進制思想”。
另有學者對中國青海樂都縣柳灣出土一千多枚新石器時代骨片進行研究,發現它們分屬馬廠、半山、齊家和辛店四個中文化型。骨片長度為2-2.4厘米,厚約1毫米。骨片上有刻痕,少的一個,多不超過八個,每個骨片上的刻痕數目不超過十個,他們以此認為新石器時代已有加法運算和十進制。
另有學者認為,甲骨文中一橫代表1,兩橫相疊代表二,三橫代表三,四橫代表四,X代表五,“人”形代表六,“十”代表七,“)(”代表八,“九”已經是九;|代表十,||代表20,|||代表三十,||||代表四十;此外50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000,2000,……9000,10000……40000都有不同的符號。商代甲骨文“已形成完整的十進制系統”。
北京的中國歷史博物館藏有一把安陽殷墟出土的象牙尺,長15.78厘米,分為十寸,說明中國商代的十進制幾經用在長度上了。
中國周代金文的紀數法,繼承商代的十進制,又有明顯的進步,十進數量級符號有十、百、千、萬、億,如西周金文“伐鬼方……俘萬三千八十一人”,“武王遂征四方,俘人三億萬有二百三十”,出現了位值記數,例如“俘牛三百五十五“,其中三百五十五寫成“三全XX”,前面的“全”是金文的“百”,後面兩個XX是五十五,省去了“十”,出現了位置概念,但尚未形成完整的位值制。金文商鞅量銘還出現分數。
春秋戰國時代,出現嚴格的十進位制籌算記數,以空代表0,也發明了用於十進位制乘法、除法的九九表<
公元前3400年左右,古埃及有基於十進制的記數法。但這種十進制並無位值的概念。
吠陀時代前800年的印度儀軌經類文獻中的繩法經中包含大量分數的套用,但並無證據顯示此時的文字記數系統是十進制的。
公元前500年,希臘古典時期的阿提卡數字為十進制系統。
公元前300年,印度的婆羅迷數字為十進制。婆羅迷十進制毫無位值概念。
出土於巴基斯坦的古印度巴克沙利手稿可能是世界上最早的包括0的“真正的”十進制系統,但它的具體時間有爭議。
與度量衡
中國十進制度量衡有久遠的歷史。公元前6世紀的一把周朝尺刻有十分之一的寸和百分之一的分。
王莽官定一百副青銅容量標準,一斛=十斗,一斗=十升,一升=10合。
傳統度量衡不是完全使用十進制,例如1斤等於16兩、1呎等於12吋等。公制完全使用十進制,使換算較直接。中華民國政府於1920年代推行市制以與公制接軌。1980年代香港政府便曾大力宣傳十進制的好處,當時有口號如“採用十進制,公道又易計”或“十進制,好易計”等,但民間至今仍常用舊制、英制等非十進制換算。
來源
人類算數採用十進制,可能跟人類有十根手指有關。亞里士多德稱人類普遍使用十進制,只不過是絕大多數人生來就有10根手指這樣一個解剖學事實的結果。實際上,在古代世界獨立開發的有文字的記數體系中,除了巴比倫文明的楔形數字為60進制,瑪雅數字為20進制外,幾乎全部為十進制。只不過,這些十進制記數體系並不是按位的。
方法
用文字表示十進整數位
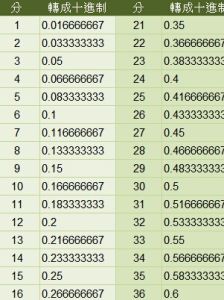
十進位制可以表示任何整數。利用小數點,還可以表示一些小數。
十進制漢字對照表
|
|
|
|
|
|
|
各國對十進制的表達形式區別
巴比倫60進位制以一個上大下小的楔形代表1,兩個並列楔形代表2,三個並列楔形代表3,上二個楔形下二個楔形代表4,上三楔下二楔代表5,上三楔下三楔代表6,上四楔下三楔代表7,上四楔下四楔代表8,上五楔下四楔代表9;一個左小右大橫楔代10,兩個橫楔並排代表20,三個橫楔並排代表30,四個橫楔並排代表40。
瑪雅20進位制以一個點代表1,兩個點並列代表2,三點並列代表3,四點並列代表4,短橫線代表5,橫線上加一點代表6,橫線上加二點代表7,橫線上加三點代表8,橫線上加四點代表9;上下兩橫線代表10,上下兩橫線之上加一點代表11,三重疊橫線代表15,三橫線上加一,二,三點代表16,17,18;小橢圓圈上加一點代表20。
古埃及十進制以一個豎道代表1,二並排豎道代表2,三豎道代表3,一橫道代表4,左二撇右豎道代表5,上三撇下三撇代表6,上下兩道代表8,四個(並排代表9,一個“人”字形代表10,“人”上加一橫代表20,20左加一點代表30,橫道上加一點代表40,橫道上加三豎道(如中國籌算的8)代表60,橫道上加四豎道代表80(形同中國籌算中的9)代表80,兩橫道上加三豎代表90……。
希臘十進制,1至9,10至90,100至900各有不同的單字母代表。
古印度Kharosshi十進制,以一個豎道代表1,二並排豎道代表2,三豎道代表3,一個X代表4,IX代表5,||X代表6,XX代表8,10,20個有單字元代表。
古印度和Brahmi十進制,和希臘十進制相似,1至9,10至90,100至900各有不同的單字母代表。符號很多。
據某些學者考證,中國古代的十進制有書寫式和算籌兩種型式。
補充說明
十進制,英文名稱為DecimalSystem,來源於希臘文Decem,意為十。十進制計數是由印度教教徒在1500年前發明的,有阿拉伯人傳承至11世紀。
十進制基於位進制和十進位兩條原則,即所有的數字都用10個基本的符號表示,滿十進一,同時同一個符號在不同位置上所表示的數值不同,符號的位置非常重要。基本符號是0到9十個數字。要表示這十個數的10倍,就將這些數字左移一位,用0補上空位,即10,20,30,...,90;要表示這十個數的10倍,就繼續左移數字的位置,即100,200,300,...。要表示一個數的1/10,就右移這個數的位置,需要時就0補上空位:1/10位0.1,1/100為0.01,1/1000為0.001。--摘自《統計學》附錄3數學基礎知識P205-6[英]提姆.漢拿根2008.1
另外同人遊戲《東方紅魔鄉》一面BOSS露米婭的綽號為“十進制”,出處為魔理沙線的對話:“為什麼總是伸直手臂?”“像不像耶穌被釘在十字架上?”“像是人類採用了十進制”
計數法
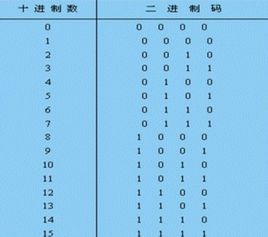
十進制計數法是相對二進制計數法而言的,是我們日常使用最多的計數方法(俗稱“逢十進一”),它的定義是:“每相鄰的兩個計數單位之間的進率都為十”的計數法則,就叫做“十進制計數法”。
所周知,計算機內部使用二進制表示數,二進制與十進制的轉換是比較複雜的。比如我們要讓計算機計算50+50=?,那么首先要把十進制的50轉換成二進制的“50”——110010,這個過程要做多次除法,而計算機對於除法的計算是最慢的。把十進制的50轉換成二進制的110010還不算完,計算出結果1100100之後還要再轉換成十進制數100,這是一個做乘法的過程,對計算機來說雖然比除法簡單,但計算速度也不快。本來一步完成的事,卻白白浪費了好多步驟,究其原因,就是人們使用的十進制不適應現代化信息設備,不是最佳信息計數法。如果人們使用二進制來表示數,不僅與計算機的交流變得簡便,而且只需要記得怎樣寫0和1就能夠記數了,比用十進制需要學習十個數字簡單了80%。這還不是全部,舉個例子來說,比如十進制的小數0.8,在二進制里怎樣表示呢?要寫成0.11001100...後面還有無數個1100,或者換句話說,十進制的有限小數轉換成二進制不能保證能精確轉換,二進制小數轉換成十進制也遇到同樣的問題。這也為信息處理帶來了很大的不便。甚至為了能夠較快的轉換十進制數和二進制數,在設計處理器的時候加入了專門的電路和語句來完成這個過程,造成了處理器設計的浪費。因此,可以說十進制不適應現代化信息設備。
轉換
二進制數轉換成十進制數
由二進制數轉換成十進制數的基本做法是,把二進制數首先寫成加權係數展開式,然後按十進制加法規則求和。這種做法稱為"按權相加"法。例1105把二進制數110.11轉換成十進制數。
十進制數轉換為二進制數
十進制數轉換為二進制數時,由於整數和小數的轉換方法不同,所以先將十進制數的整數部分和小數部分分別轉換後,再加以合併。
1.十進制整數轉換為二進制整數十進制整數轉換為二進制整數採用"除2取余,逆序排列"法。具體做法是:用2去除十進制整數,可以得到一個商和餘數;再用2去除商,又會得到一個商和餘數,如此進行,直到商為零時為止,然後把先得到的餘數作為二進制數的低位有效位,後得到的餘數作為二進制數的高位有效位,依次排列起來。
2.十進制小數轉換為二進制小數
十進制小數轉換成二進制小數採用"乘2取整,順序排列"法。具體做法是:用2乘十進制小數,可以得到積,將積的整數部分取出,再用2乘餘下的小數部分,又得到一個積,再將積的整數部分取出,如此進行,直到積中的小數部分為零,或者達到所要求的精度為止。
然後把取出的整數部分按順序排列起來,先取的整數作為二進制小數的高位有效位,後取的整數作為低位有效位。
交流平台
邪惡十進制邪惡十進制信息安全團隊(EvilDecimal簡稱:E.T.A)創立與二零零九年十月十六日,是由來自五湖四海的網路安全愛好者組成,以普及提升全民網路安全意識為主,推動網路安全文化為準。提供了真正免費的網路安全技術學習資料,讓更多的安全技術愛好者,從中吸取技術元素,全方面提高安全技術水平,做到普及網路安全技術之目標,同時也為大家搭建一個技術交流平台。