研究歷史
阿波羅尼奧斯所著的八冊《圓錐曲線論(Conics)》中首次提出了今日大家熟知的 ellipse(橢圓)、parabola(拋物線)、hyperbola(雙曲線)等與圓錐截線有關的名詞,可以說是古希臘幾何學的精擘之作。
直到十六、十七世紀之交,克卜勒(Kepler)行星運行三定律的發現才知道行星繞太陽運行的軌道,是一種以太陽為其一焦點的橢圓。
定義
第一定義
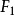 橢圓
橢圓平面內與兩定點
、
的距離的和等於常數
(
)的動點P的軌跡叫做橢圓。
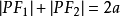 橢圓
橢圓即:
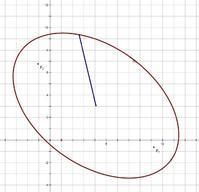 橢圓
橢圓其中兩定點
、
叫做橢圓的焦點,兩焦點的距離
叫做橢圓的焦距。
為橢圓的動點。
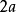 橢圓
橢圓橢圓截與兩焦點連線重合的直線所得的弦為長軸,長為
 橢圓
橢圓橢圓截垂直平分兩焦點連線的直線所得弦為短軸,長為
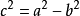 橢圓
橢圓可變為
第二定義
 橢圓
橢圓橢圓平面內到定點
(c,0)的距離和到定直線
:
(
不在
上)的距離之比為常數
(即離心率
,0<1)的點的軌跡是橢圓。
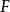 橢圓
橢圓其中定點
為橢圓的焦點
,定直線
稱為橢圓的準線(該定直線的方程是
(焦點在x軸上),或
(焦點在y軸上))。
其他定義
 橢圓
橢圓根據橢圓的一條重要性質:橢圓上的點與橢圓長軸兩端點連線的斜率之積是定值,定值為
,可以得出:
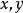 橢圓
橢圓在坐標軸內,動點(
)到兩定點(
)(
)的斜率乘積等於常數m(-1<0)
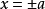 橢圓
橢圓注意:考慮到斜率為零時不滿足乘積為常數,所以
無法取到,即該定義僅為去掉兩個點的橢圓。
橢圓也可看做圓按一定方向作壓縮或拉伸一定比例所得圖形。
方程
中心點為(h,k),主軸平行於x軸時,
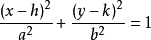 橢圓
橢圓標準方程
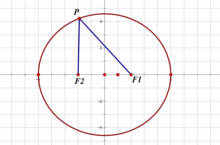 F點在X軸
F點在X軸高中課本在平面直角坐標系中,用方程描述了橢圓,橢圓的標準方程中的“標準”指的是中心在原點,對稱軸為坐標軸。
橢圓的標準方程有兩種,取決於焦點所在的坐標軸:
1)焦點在X軸時,標準方程為:x²/a²+y²/b²=1 (a>b>0)
2)焦點在Y軸時,標準方程為:y²/a²+x²/b²=1 (a>b>0)
橢圓上任意一點到F1,F2距離的和為2a,F1,F2之間的距離為2c。而公式中的b²=a²-c²。b是為了書寫方便設定的參數。
又及:如果中心在原點,但焦點的位置不明確在X軸或Y軸時,方程可設為mx²+ny²=1(m>0,n>0,m≠n)。即標準方程的統一形式。
橢圓的面積是πab。橢圓可以看作圓在某方向上的拉伸,它的參數方程是:x=acosθ , y=bsinθ
標準形式的橢圓在(x0,y0)點的切線就是 :xx/a²+yy/b²=1。橢圓切線的斜率是:-b²x/a²y,這個可以通過很複雜的代數計算得到。
參數方程
x=acosθ , y=bsinθ。
求解橢圓上點到定點或到定直線距離的最值時,用參數坐標可將問題轉化為三角函式問題求解
x=a×cosβ, y=b×sinβ a為長軸長的一半
極坐標
(一個焦點在極坐標系原點,另一個在θ=0的正方向上)
r=a(1-e²)/(1-ecosθ)
(e為橢圓的離心率=c/a)
幾何性質
基本性質
 橢圓
橢圓1、範圍:焦點在
軸上
,
;焦點在
軸上
,
2、對稱性:關於X軸對稱,Y軸對稱,關於原點中心對稱。
3、頂點:(a,0)(-a,0)(0,b)(0,-b)
 橢圓
橢圓4、離心率:
或 e=√(1-b^2/a²)
5、離心率範圍:0<1
6、離心率越大橢圓就越扁,越小則越接近於圓。
7、焦點(當中心為原點時):(-c,0),(c,0)或(0,c),(0,-c)
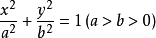 橢圓
橢圓8、
與
(m為實數)為離心率相同的橢圓。
9、P為橢圓上的一點,a-c≤PF1(或PF2)≤a+c。
切線法線
定理1:設F1、F2為橢圓C的兩個焦點,P為C上任意一點。若直線AB切橢圓C於點P,且A和B在直線上位於P的兩側,則∠APF1=∠BPF2。
定理2:設F1、F2為橢圓C的兩個焦點,P為C上任意一點。若直線AB為C在P點的法線,則AB平分∠F1PF2。
上述兩定理的證明可以查看參考資料。
光學性質
橢圓的面鏡(以橢圓的長軸為軸,把橢圓轉動180度形成的立體圖形,其外表面全部做成反射面,中空)可以將某個焦點發出的光線全部反射到另一個焦點處;橢圓的透鏡(某些截面為橢圓)有匯聚光線的作用(也叫凸透鏡),老花眼鏡、放大鏡和遠視眼鏡都是這種鏡片(這些光學性質可以通過反證法證明)。
-----關於圓錐截線的某些歷史:圓錐截線的發現和研究起始於古希臘。 Euclid, Archimedes, Apollonius, Pappus 等幾何學大師都熱衷於圓錐截線的研究,而且都有專著論述其幾何性質,其中以 Apollonius 所著的八冊《圓錐截線論》集其大成,可以說是古希臘幾何學一個登峰造極的精擘之作。當時對於這種既簡樸又完美的曲線的研究,乃是純粹從幾何學的觀點,研討和圓密切相關的這種曲線;它們的幾何乃是圓的幾何的自然推廣,在當年這是一種純理念的探索,並不寄望也無從預期它們會真的在大自然的基本結構中扮演著重要的角色。此事一直到十六、十七世紀之交,Kepler 行星運行三定律的發現才知道行星繞太陽運\行的軌道,乃是一種以太陽為其一焦點的橢圓。Kepler 三定律乃是近代科學開天劈地的重大突破,它不但開創了天文學的新紀元,而且也是牛頓萬有引力定律的根源所在。由此可見,圓錐截線不單單是幾何學家所愛好的精簡事物,它們也是大自然的基本規律中所自然選用的精要之一。
相關公式
面積公式
 橢圓
橢圓(其中
分別是橢圓的長半軸、短半軸的長),或
(其中
分別是橢圓的長軸,短軸的長)。
周長
橢圓周長計算公式:L=T(r+R)
T為橢圓係數,可以由r/R的值,查表找出係數T值;r為橢圓短半徑;R為橢圓長半徑。
橢圓周長定理:橢圓的周長等於該橢圓短半徑與長半徑之和與該橢圓係數的積(包括正圓)。
附橢圓係數簡表:
| 橢圓係數簡表 | |||||||
| r / R | 係數 | r / R | 係數 | r / R | 係數 | r / R | 係數 |
| 0.01 | 3.961483495 | 0.26 | 3.418920439 | 0.51 | 3.224856225 | 0.76 | 3.156214217 |
| 0.02 | 3.925332509 | 0.27 | 3.40695685 | 0.52 | 3.220415735 | 0.77 | 3.154868403 |
| 0.03 | 3.891174223 | 0.28 | 3.395457698 | 0.53 | 3.216154903 | 0.78 | 3.153601776 |
| 0.04 | 3.858791647 | 0.29 | 3.384403803 | 0.54 | 3.212067616 | 0.79 | 3.152411903 |
| 0.05 | 3.828024399 | 0.3 | 3.373776976 | 0.55 | 3.208148 | 0.8 | 3.151296432 |
| 0.06 | 3.798743616 | 0.31 | 3.363559954 | 0.56 | 3.204390411 | 0.81 | 3.150253089 |
| 0.07 | 3.770841059 | 0.32 | 3.353736335 | 0.57 | 3.200789422 | 0.82 | 3.149279677 |
| 0.08 | 3.744223265 | 0.33 | 3.344290532 | 0.58 | 3.197339815 | 0.83 | 3.148374067 |
| 0.09 | 3.718808013 | 0.34 | 3.335207712 | 0.59 | 3.194036571 | 0.84 | 3.147534204 |
| 0.1 | 3.694521982 | 0.35 | 3.326473758 | 0.6 | 3.190874858 | 0.85 | 3.146758097 |
| 0.11 | 3.671299121 | 0.36 | 3.318075219 | 0.61 | 3.187850029 | 0.86 | 3.146043822 |
| 0.12 | 3.649079455 | 0.37 | 3.309999276 | 0.62 | 3.184957608 | 0.87 | 3.145389514 |
| 0.13 | 3.627808177 | 0.38 | 3.302233702 | 0.63 | 3.182193286 | 0.88 | 3.144793371 |
| 0.14 | 3.607434941 | 0.39 | 3.294766828 | 0.64 | 3.179552911 | 0.89 | 3.144253646 |
| 0.15 | 3.587913299 | 0.4 | 3.287587514 | 0.65 | 3.177032484 | 0.9 | 3.143768649 |
| 0.16 | 3.569200238 | 0.41 | 3.280685115 | 0.66 | 3.174628151 | 0.91 | 3.143336742 |
| 0.17 | 3.551255799 | 0.42 | 3.274049459 | 0.67 | 3.172336195 | 0.92 | 3.14295634 |
| 0.18 | 3.534042762 | 0.43 | 3.267670819 | 0.68 | 3.170153034 | 0.93 | 3.142625907 |
| 0.19 | 3.517526368 | 0.44 | 3.261539886 | 0.69 | 3.168075214 | 0.94 | 3.142343956 |
| 0.2 | 3.50167409 | 0.45 | 3.255647754 | 0.7 | 3.166099401 | 0.95 | 3.142109044 |
| 0.21 | 3.486455429 | 0.46 | 3.249985893 | 0.71 | 3.164222379 | 0.96 | 3.141919775 |
| 0.22 | 3.471841741 | 0.47 | 3.244546132 | 0.72 | 3.162441046 | 0.97 | 3.141774794 |
| 0.23 | 3.457806077 | 0.48 | 3.239320639 | 0.73 | 3.160752407 | 0.98 | 3.141672788 |
| 0.24 | 3.444323049 | 0.49 | 3.234301909 | 0.74 | 3.159153568 | 0.99 | 3.141612486 |
| 0.25 | 3.43136871 | 0.5 | 3.22948274 | 0.75 | 3.157641737 | 1 | π |
| 工程運用橢圓係數簡表 | |||||||
| r / R | 係數 | r / R | 係數 | r / R | 係數 | r / R | 係數 |
| 1 | π | 0.4787 | 3.24 | 0.2011 | 3.5 | 0.0739 | 3.76 |
| 0.9555 | 3.142 | 0.4599 | 3.25 | 0.1946 | 3.51 | 0.0703 | 3.77 |
| 0.9188 | 3.143 | 0.4422 | 3.26 | 0.1884 | 3.52 | 0.0666 | 3.78 |
| 0.8951 | 3.144 | 0.4263 | 3.27 | 0.1824 | 3.53 | 0.0631 | 3.79 |
| 0.8764 | 3.145 | 0.4111 | 3.28 | 0.1764 | 3.54 | 0.0595 | 3.8 |
| 0.8607 | 3.146 | 0.3966 | 3.29 | 0.1707 | 3.55 | 0.0561 | 3.81 |
| 0.8468 | 3.147 | 0.3829 | 3.3 | 0.1651 | 3.56 | 0.0526 | 3.82 |
| 0.8433 | 3.148 | 0.3699 | 3.31 | 0.1595 | 3.57 | 0.0493 | 3.83 |
| 0.8231 | 3.149 | 0.3577 | 3.32 | 0.1541 | 3.58 | 0.0461 | 3.84 |
| 0.8126 | 3.15 | 0.3459 | 3.33 | 0.1489 | 3.59 | 0.0428 | 3.85 |
| 0.7689 | 3.155 | 0.3414 | 3.34 | 0.1437 | 3.6 | 0.0396 | 3.86 |
| 0.7347 | 3.16 | 0.3239 | 3.35 | 0.1387 | 3.61 | 0.0364 | 3.87 |
| 0.7058 | 3.165 | 0.3136 | 3.36 | 0.1337 | 3.62 | 0.0333 | 3.88 |
| 0.6806 | 3.17 | 0.3036 | 3.37 | 0.1289 | 3.63 | 0.0303 | 3.89 |
| 0.6584 | 3.175 | 0.2941 | 3.38 | 0.1242 | 3.64 | 0.0273 | 3.9 |
| 0.6383 | 3.18 | 0.2848 | 3.39 | 0.1195 | 3.65 | 0.0244 | 3.91 |
| 0.6199 | 3.185 | 0.2759 | 3.4 | 0.1149 | 3.66 | 0.0215 | 3.92 |
| 0.6028 | 3.19 | 0.2674 | 3.41 | 0.1105 | 3.67 | 0.0186 | 3.93 |
| 0.5871 | 3.195 | 0.2591 | 3.42 | 0.1062 | 3.68 | 0.0158 | 3.94 |
| 0.5722 | 3.2 | 0.2511 | 3.43 | 0.1019 | 3.69 | 0.0131 | 3.95 |
| 0.5583 | 3.205 | 0.2432 | 3.44 | 0.0977 | 3.7 | 0.0103 | 3.96 |
| 0.5452 | 3.21 | 0.2357 | 3.45 | 0.0935 | 3.71 | 0.0077 | 3.97 |
| 0.5328 | 3.215 | 0.2284 | 3.46 | 0.0895 | 3.72 | 0.0051 | 3.98 |
| 0.5097 | 3.225 | 0.2212 | 3.47 | 0.0855 | 3.73 | 0.0025 | 3.99 |
| 0.4989 | 3.23 | 0.2143 | 3.48 | 0.0816 | 3.74 | 0.0012 | 3.995 |
| 0.4886 | 3.235 | 0.2076 | 3.49 | 0.0777 | 3.75 | 0.0002 | 3.999 |
離心率
橢圓離心率的定義為橢圓上焦距與長軸的比值,(範圍:0<1)
e=c/a(0<1),因為2a>2c。離心率越大,橢圓越扁平;離心率越小,橢圓越接近於圓形。
橢圓的焦準距:橢圓的焦點與其相應準線(如焦點(c,0)與準線x=±a^2/c) 的距離為a^2/c-c=b^2/c
 橢圓
橢圓離心率與
的關係:
焦半徑
焦點在x軸上:|PF1|=a+ex |PF2|=a-ex(F1,F2分別為左右焦點)
橢圓過右焦點的半徑r=a-ex
過左焦點的半徑r=a+ex
焦點在y軸上:|PF1|=a+ey |PF2|=a-ey(F2,F1分別為上下焦點)
橢圓的通徑:過焦點的垂直於x軸(或y軸)的直線與橢圓的兩交點A,B之間的距離,即|AB|=2*b^2/a
斜率公式
過橢圓上x²/a²+y²/b²=1上一點(x,y)的切線斜率為 -b²X/a²y
三角面積
若有一三角形兩個頂點在橢圓的兩個焦點上,且第三個頂點在橢圓上
那么若∠FPF=θ,則S=b²tan(θ/2)。
曲率公式
K=ab/[(b²-a²)(cosθ)+a²]
準線方程
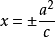 橢圓
橢圓(焦點在x軸上)
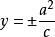 橢圓
橢圓(焦點在y軸上)
準圓方程
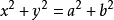 橢圓
橢圓準圓為
從準圓上任一點向橢圓引兩條切線,這兩條切線垂直。
通徑
l=2b^2/a
圓錐曲線(除圓外)中,過焦點並垂直於軸的弦
橢圓中的通徑是通過焦點最短的弦
幾何關係
點與橢圓
 合併圖冊
合併圖冊點M(x0,y0) 橢圓 x^2/a^2+y^2/b^2=1
點在圓內:x/a+y/b<1
點在圓上:x/a+y/b=1
點在圓外:x/a+y/b>1
跟圓與直線的位置關係一樣的
相交 相離 相切
直線與橢圓
y=kx+m ①
x/a+y/b=1 ②
由①②可推出xa+(kx+m)/b=1
相切△=0
相離△<0無交點
相交△>0 可利用弦長公式:設A(x,y) B(x,y)
求中點坐標
根據韋達定理 x+x=-b/a,xx=c/a
帶入直線方程可求出 (y+y)/2=可求出中點坐標。
|AB|=d = √(1+k)[(x+x)-4x1*x2] = √(1+1/k)[(y+y)-4yy]
套用
例如:有一個圓柱,被截得到一個截面,下面證明它是一個橢圓(用上面的第一定義):
將兩個半徑與圓柱半徑相等的半球從圓柱兩端向中間擠壓,它們碰到截面的時候停止,那么會得到兩個公共點,顯然他們是截面與球的切點。
設兩點為F1、F2
對於截面上任意一點P,過P做圓柱的母線Q1、Q2,與球、圓柱相切的大圓分別交於Q1、Q2
則PF1=PQ1、PF2=PQ2,所以PF1+PF2=Q1Q2
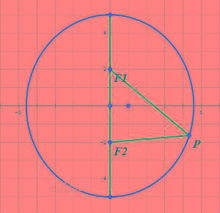 橢圓
橢圓由定義1知:截面是一個橢圓,且以F1、F2為焦點
用同樣的方法,也可以證明圓錐的斜截面(不通過底面)為一個橢圓
例:已知橢圓C:x^2/a^2+y^2/b^2=1(a>b>0)的離心率為√6/3,短軸一個端點到右焦點的距離為√3.
1.求橢圓C的方程.
2.直線l:y=x+1與橢圓交於A,B兩點,P為橢圓上一點,求△PAB面積的最大值.
3.在⑵的基礎上求△AOB的面積.
一 分析短軸的端點到左右焦點的距離和為2a,端點到左右焦點的距離相等(橢圓的定義),可知a=√3,又c/a=√6/3,代入得c=√2,b=√(a^2-c^2)=1,方程是x^2/3+y^2/1=1,
二 要求面積,顯然以ab作為三角形的底邊,聯立x^2/3+y^2/1=1,y=x+1解得x1=0,y1=1,x2=-1.5,y2=-0.5.利用弦長公式有√(1+k^2))[x2-x1](中括弧表示絕對值)弦長=3√2/2,對於p點面積最大,它到弦的距離應最大,假設已經找到p到弦的距離最大,過p做弦的平行線,可以 發現這個平行線是橢圓的切線是才會最大,這個切線和弦平行故斜率和弦的斜率=,設y=x+m,利用判別式等於0,求得m=2,-2.結合圖形得m=-2.x=1.5,y=-0.5,p(1.5,-0.5),
三 直線方程x-y+1=0,利用點到直線的距離公式求得√2/2,面積1/2*√2/2*3√2/2=3/4,
手工畫法
手繪法一
畫長軸AB,短軸CD,AB和CD互垂平分於O點。⑵:連線AC。⑶:以O為圓心,OA為半徑作圓弧交OC延長線於E點。⑷:以C為圓心,CE為半徑作圓弧與AC交於F點。⑸:作AF的垂直平分線交CD延長線於G點,交AB於H點。⑹:截取H,G對於O點的對稱點H’,G’ ⑺:H,H’為長軸圓心,分別以HA、H‘B為半徑作圓;G,G’為短軸原心,分別以GC、G‘D為半徑作圓。
用一根線或者細銅絲,鉛筆,2個圖釘或大頭針畫橢圓的方法:先畫好長短軸的十字線,在長軸上以圓點為中心先找2個大於短軸半徑的點,一個點先用圖釘或者大頭針栓好線固定住,另一個點的線先不要固定,用筆帶住線去找長短軸的4個頂點,此步驟需要多次定位,直到都正好能於頂點吻合後固定住這2個點,用筆帶住線,直接畫出橢圓:)使用細銅絲最好,因為線的彈性較大畫出來不一定準確!
手繪法二
 已知長軸與短軸尺寸,兩焦點焦距尺規作圖法
已知長軸與短軸尺寸,兩焦點焦距尺規作圖法橢圓的焦距│FF'│(Z)定義,為已知橢圓所構成的長軸X(a
b)與短軸Y(cd)則以長軸一端A為圓心短軸Y為半徑畫弧,從長軸另一段點B引出與弧相切的線段則為該橢圓焦距,求證公式為2√{(Z/2)^2+(Y/2)^2}+Z=X+Z(平面內與兩定點F、F'的距離的和等於常數2a(2a>|FF'|)的動點P的軌跡叫做橢圓),可演變為z=√x^2-y^2(x>y>0)。Z兩端點F、F'為定點。取有韌性切伸縮係數越小越好的線,環繞線段AF'或者FB線段任意一組為長度,以該長度為固定三角形周長,以F、F'為定點、取構成該三角形上的第三點為動點畫弧則構成該橢圓。
手繪法三
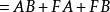 橢圓
橢圓環線長
。根據橢圓的圖形特徵,採用環線表示動點與焦點間的距離關係,形成統一的圓形環線作圖法。具體方法簡介:(1)作圖工具為筆、大頭針、直尺和環形線。(環形線製作:取一段長度(30—50cm)和粗細適中彈性小的軟線、一段8mm長細電線空塑膠管,軟線從塑膠管中相向竄過,塑膠管將軟線夾緊,但用力可以抽動,形成能收縮和放長的環形線)。(2)在作圖平面上作出各種圓形的定點和動點。(3)將大頭針分別直立、固定在定點上;(4)將符合長度的環形線套在大頭針外,畫筆由內向外拉直環線,通過調整環線的長度使筆尖剛好落在動點上;(5)將畫筆移動一周,即可作出各種圓的圖形。
環線作圖方法的最大特點,就是把圓形的動點與焦點間的距離關係以環線的方式聯繫起來,而不受焦點數目的影響,環線內可以容納任意焦點數目,為探討3個及其3個以上焦點數目的多焦點圓提供有效方法。環線作圖方法,屬於連續移動作圖法,適合不同大小的圓、橢圓和卵圓等作圖。
計算機方面
Ellipse函式
函式功能
該函式用於畫一個橢圓,橢圓的中心是限定矩形的中心,使用當前畫筆畫橢圓,用當前的畫刷填充橢圓。
函式原型
BOOL Ellipse(HDC hdc,int nLeftRect,int nTopRect,nRightRect,int nBottomRect).
參數
hdc:設備環境句柄。
nLeftRect:指定限定橢圓左上角的X坐標。
nTopRect:指定限定橢圓左上角的Y坐標。
nRightRect:指定限定橢圓右下角的X坐標。
nBottomRect:指定限定橢圓右下角的Y坐標。
返回值
如果函式調用成功,返回值非零;如果函式調用失敗,返回值是0。
計算機圖形學約束
橢圓必須一條直徑與x軸平行,另一條直徑y軸平行。不滿足此條件的幾何學橢圓在計算機圖形學上視作一般封閉曲線。
