面積
1、由中點向各頂點連線得到8個等腰三角形，設八邊形最長對角線為2a，則等腰三角形腰長a，用正弦定理計算三角形的面積。得1/2*a*a*sin(360/2a)=2a*sin45，所以正八邊形的面積為8*2a*sin45。
2、設正八邊形內最長對角線長為a，最短對角線長為b，則正八邊形面積面積為ab。
3、已知邊長為a時，又有：S=(2+2√2)a²≈4.828a²。推導：正八邊形可以分割成四個小三角形，四個小長方形以及中央部分的一個正方形。四個小三角形的面積和為：(√2/2a)*(√2/2a)*1/2*4=a²，四個小長方形面積之和為：(√2/2a)*a*4=(2√2)*a²，中間的正方形面積為a²，所以正八邊形面積公式為：a²+（2√2）*a²+a²=（2+2√2）*a²
4、已經中心點到各邊的長r，則正八邊形面積為2√2r².
周長
邊長長度乘以8，即可。
尺規作圖
用直尺和圓規畫正八邊形的方法如下：
正八邊形做正方形ABCD，並做正方形外接圓O.
過圓心O向任意一邊(設為AB)作垂線並延長，延長線交圓弧於E、F.
以AE、DE為半徑畫弧，得到與圓O的交點，分別為G、H.
連線EAGBFCHD.
擦除其他對象，即得正八邊形EAGBFCHD.
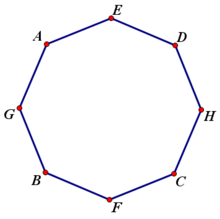正八邊形正八邊形