介紹
有理函式是通過多項式的加減乘除得到的函式。
在數學中,理性函式是可以由有理分數定義的任何函式,即代數分數,使得分子和分母都是多項式。 多項式的係數不需要是有理數,它們可以在任何欄位K中進行。變數的情況可以在包含K的任何欄位L中進行。函式的域是變數,分母不為零,代碼區為L。
一個有理函式h可以寫成如下形式:h=f/g,這裡 f 和 g 都是多項式函式。有理函式是特殊的亞純函式, 它的零點和極點個數有限。
有理函式全體構成所謂的有理函式域。
在實數範圍內,無限不循環的小數叫做無理數,一般通過開平方得到。在二次函數裡面,如 y=a*x^2+b*x+c,如果△≥0,那么 y=0 有實數解;如果△<0,那么 y=0 沒有實數解,但有虛數解。
定義
函式f(x)被稱為理性函式,若且唯若它可以以表單形式:
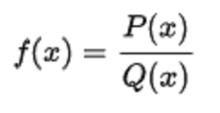 有理函式
有理函式其中P和Q是x中的多項式,Q不是零多項式。域f是所有點x的集合,分母Q(x)不為零。
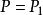 有理函式
有理函式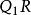 有理函式
有理函式但是,如果P和Q具有非常數多項式最大公約數R,則設定R和Q=滿足:
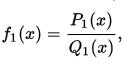 有理函式
有理函式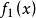 有理函式
有理函式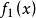 有理函式
有理函式其可以具有比f(x)更大的域,並且等於f(x)的域上的f (X)域。 識別f(x)和是一種常見的用法,即擴展“連續性” f(x)為。 實際上,可以將合理的分數定義為多項式分數的等價類,其中兩個分數:
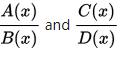 有理函式
有理函式當
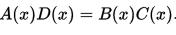 有理函式
有理函式被認為是等價的。
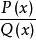 有理函式
有理函式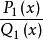 有理函式
有理函式在這種情況下和是等價的。
舉例
有理函式
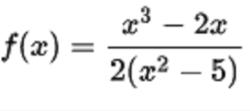 有理函式
有理函式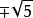 有理函式
有理函式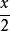 有理函式
有理函式沒有在x=中定義。當x逼近無窮大時,它是漸近於的。
理性函式
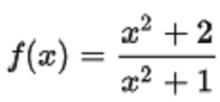 有理函式
有理函式定義為所有實數,但不適用於所有複數,因為如果x是-1的平方根(即虛數單位或其負數),則正式評估將導致被零除,
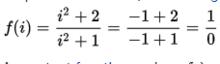 有理函式
有理函式這是未定義的。
常數函式如f(x)=π是一個有理函式,因為常數是多項式。請注意,函式本身是理性的,即使f(x)的值對於所有x都是不合理的。
 有理函式
有理函式當Q(x)=1時,每個多項式函式f(x)=是有理函式。不能以這種形式寫入的函式,如f(x)= \sin(x)形容詞“不合理”通常不用於功能。
 有理函式
有理函式對於除0之外的所有x,理性函式f(x)=等於1,一個可移動的奇點。兩個理性函式的和,乘積或商(除零次多項式)本身就是一個理性函式。然而,除非要注意,否則減少到標準形式的過程可能會無意中導致除去這些奇異點。使用有理函式的定義作為等價類來解決這個問題,因為x / x等於1/1。
泰勒級數
任何有理函式的泰勒級數的係數滿足線性遞推關係,可以通過設定等價於其泰勒級數的合理函式和收集類似項來找到。
例如,
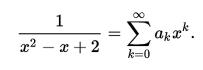 有理函式
有理函式乘以分母並整理得,
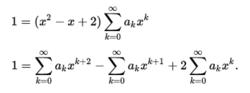 有理函式
有理函式在調整總和的索引以獲得相同的x的權力後,我們得到,
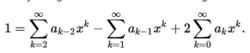 有理函式
有理函式結合類似術語給出:
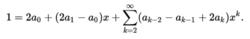 有理函式
有理函式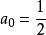 有理函式
有理函式由於這對於原始泰勒級數的收斂半徑中的所有x都是正確的,所以我們可以計算如下。 由於左邊的常數值必須等於右邊的常數項。
那么,由於在左邊沒有x的係數,所以右邊的所有係數都必須為零,從而遵循這一點:
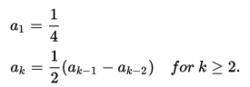 有理函式
有理函式相反,當用作泰勒級數的係數時,滿足線性重複的任何序列確定有理函式。 這在解決這種復現中是有用的,因為通過使用部分分數分解,我們可以寫出任何有理函式作為1 /(ax + b)形式的因子的總和,並將其擴展為幾何系列,給出泰勒係數的顯式公式; 這是生成函式的方法。
代數和幾何
在抽象代數中,多項式的概念被擴展為包括可以從任何欄位獲取多項式的係數的形式表達式。在給定場F和一些不確定X的這個設定中,有理表達式是多項式環F [X]的分數場的任何元素。任何合理的表達式都可以被寫為具有Q≠0的兩個多項式P / Q的商,儘管該表示不是唯一的。當PS = QR時,P / Q等於R / S,對於多項式P,Q,R和S。然而,由於F [X]是唯一的因式分解域,對於任何理性表達式P / Q,存在具有最低度的P和Q多項式的Q / Q的唯一表示,並且Q選為monic。這類似於通過取消常見因素,通常可以以最低的值唯一地寫入整數的一部分。
理性表達領域被表示為F(X)。據說這個欄位是通過(超越元素)X生成的(作為一個欄位),因為F(X)不包含含有F和元素X的任何適當的子欄位。
複雜有理函式
在複雜的分析中,有理函式:
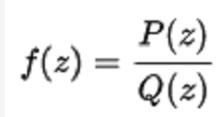 有理函式
有理函式是具有復係數的兩個多項式的比率,其中Q不是零多項式,P和Q沒有公共因子(這避免了f取不確定值0/0)。 f的域和範圍通常被認為是黎曼球體,這避免了在函式極點(其中Q(z)為0)的特殊處理的任何需要。
有理函式的程度是其組成多項式P和Q的度數的最大值。如果f的程度為d,則方程f(z)=w在z中有不同的解決方案,除了w的某些值,稱為臨界值,其中兩個或多個解決方案相符。具有1級的理性函式稱為莫比斯變換,並形成了黎曼球的自動組。 理性函式是擬態函式的代表性例子。
相關概念
像多項式一樣,理性表達式也可以通過將F(X1,...,Xn)的分數的領域F(X1,...)表示為n個不確定的X1,...,Xn,XN)。
在代數幾何中使用理性函式的抽象概念的擴展版本。 其中代數變數V的函式域形成為V坐標環的分數的場(更準確地說是在V中的Zariski密集仿射開放集合)。 其元素f被認為是在非空開放集U的代數幾何學意義上的常規函式,並且也可以被視為投影線的態射。
套用
這些對象首先在學校代數中遇到。在更高級的數學中,他們在環形理論中發揮重要作用,特別是在現場擴展的建設中。他們還提供了一個nonarchimedean領域的例子。
在函式的插值和近似的數值分析中使用Rational函式,例如HenriPadé介紹的Padé近似。關於理性函式的近似非常適合於計算機代數系統和其他數值軟體。像多項式一樣,它們可以被直接評估,並且同時它們表現出比多項式更多樣化的行為。
理性函式用於近似或模擬科學和工程中更複雜的方程,包括物理學領域和力量,分析化學中的光譜學,生物化學中的酶動力學,電子電路,空氣動力學,體內藥物濃度,原子和分子的波函式,光學和攝影,以提高圖像解析度,聲學和聲音[需要引用]。
在信號處理中,具有無限脈衝回響的常用線性時不變系統(濾波器)的脈衝回響的拉普拉斯變換(用於連續系統)或z變換(用於離散時間系統)是複數的理性函式。
