來歷
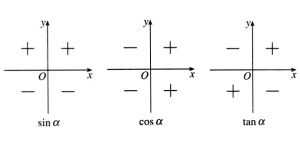 三角函式
三角函式希臘的數學轉入印度,阿耶波多作了重大的改革。一方面他定半徑為3438,含有弧度制的思想。另一方面他計算半弦(相當於現在的正弦線)而不是希臘人的全弦。他稱半弦為jiva,是獵人弓弦的意思。後來印度的書籍被譯成阿拉伯文,jiva被音譯成jiba,但此字在阿拉伯文中沒有意義,輾轉傳抄,又被誤寫成jaib,意思是胸膛或海灣。12世紀,歐洲人從阿拉伯的文獻中尋求知識。1150年左右,義大利翻譯家傑拉德將jaib意譯為拉丁文sinus,這就是現存sine一詞的來源。英文保留了sinus這個詞,意義也不曾變。
sinus並沒有很快地被採用。同時並存的正弦符號還有Perpendiculum(垂直線),表示正弦的符號並不統一。計算尺的設計者岡特在他手畫的圖上用sin表示正弦,後來,英國的奧特雷德也使用了sin這一縮寫,同時又簡寫成S。與此同時,法國的埃里岡在《數學教程》中引入了一整套數學符號,包括sin,但仍然沒有受到同時代人的注意。直到18世紀中葉,逐漸趨於統一sin。餘弦符號ces,也在18世紀變成現在cos。
三角函式符號
毛羅利科早於1558年已採用三角函式符號(Signsfortrigonometricfunctions),但當時並無函式概念,於是只稱作三角線(trigonometriclines)。他以sinus1marcus表示正弦,以sinus2marcus表示餘弦。而首個真正使用簡化符號表示三角線的人是T.芬克。他於1583年,創立以“tangent”(正切)及“secant”(正割)表示相應之概念,其後他分別以符號“sin.”,“tan.”,“sec.”,“sin.com”,“tan.com”,“sec.com”表示正弦,正切,正割,餘弦,餘切,餘割,首三個符號與現代之符號相同。後來的符號多有變化,下列的表便顯示了它們之發展變化。
使用者年代正弦餘弦正切餘切正割餘割備註
羅格蒙格努斯1622S.R.T.(Tang)T.cplSecSec.Compl
吉拉爾1626tansec.
傑克1696s.cos.t.cot.sec.cosec.
歐拉1753sin.cos.tag(tg).cot.sec.cosec
謝格內1767sin.cos.tan.cot.Ⅰ
巴洛1814sincos.tan.cot.seccosecⅠ
施泰納1827tgⅡ
皮爾斯1861sincos.tan.cotallseccosec
奧萊沃爾1881sincostancotseccscⅠ
申弗利斯1886tgctgⅡ
萬特沃斯1897sincostancotseccscⅠ
舍費爾斯1921sincostgctgseccsc
註:
Ⅰ-現代(歐洲)大陸派三角函式符號。
Ⅱ-現代英美派三角函式符號
我國現正採用Ⅱ類三角函式符號。
1729年,丹尼爾.伯努利是先以符號表示反三角函式,如以AS表示反正弦。1736年歐拉以At表示反正切,一年後又以Asinb/c表示於單位圓上正弦值相等於b/c的弧。
1772年,C.申費爾以arc.tang.表示反正切;同年,拉格朗日采以arc.sin1/1+α表示反正弦函式。1776年,蘭伯特則以arc.sin表示同樣意思。1794年,鮑利以Arc.sin表示反正弦函式。其後這些記法逐漸得到普及,去掉符號中之小點,便成現今通用之符號,如arcsinx,arccosx等。於三角函式前加arc表示反三角函式,而有時則改以於三角函式前加大寫字母開頭Arc,以表示反三角函式之主值。
另一較常用之反三角函式符號如sin-1x,tan-1x等,是赫謝爾於1813年開始採用的,把反三角函式符號與反函式符號統一起來,至今亦有套用。〔若對各三角函式的符號演變史感興趣,可參梁宗巨(1995),《數學歷史典故》,頁100-108,台北:九章出版社。〕
三角函式公式表
誘導公式
sin(-a)=-sin(a)
cos(-a)=cos(a)
sin(pi/2-a)=cos(a)
cos(pi/2-a)=sin(a)
sin(pi/2+a)=cos(a)
cos(pi/2+a)=-sin(a)
sin(pi-a)=sin(a)
cos(pi-a)=-cos(a)
sin(pi+a)=-sin(a)
cos(pi+a)=-cos(a)
tgA=tanA=sinA/cosA
兩角和與差的三角函式
sin(a+b)=sin(a)cos(b)+cos(α)sin(b)
cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))
tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))
三角函式和差化積公式
sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)
sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)
cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)
cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)
積化和差公式
sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]
cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]
sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]
二倍角公式
sin(2a)=2sin(a)cos(a)
cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)
半角公式
sin^2(a/2)=(1-cos(a))/2
cos^2(a/2)=(1+cos(a))/2
tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))
萬能公式
sin(a)=(2tan(a/2))/(1+tan^2(a/2))
cos(a)=(1-tan^2(a/2))/(1+tan^2(a/2))
tan(a)=(2tan(a/2))/(1-tan^2(a/2))
其它公式
a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)[其中,tan(c)=b/a]
a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)[其中,tan(c)=a/b]
1+sin(a)=(sin(a/2)+cos(a/2))^2
1-sin(a)=(sin(a/2)-cos(a/2))^2
其他非重點三角函式
csc(a)=1/sin(a)
sec(a)=1/cos(a)
雙曲函式
sinh(a)=(e^a-e^(-a))/2
cosh(a)=(e^a+e^(-a))/2
tgh(a)=sinh(a)/cosh(a)

