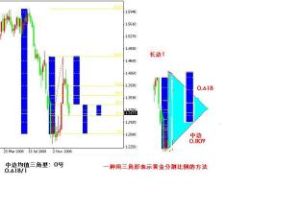
均值中邊三角形是對三條邊進行了界定的三角型，它的長邊短邊和一個介於其中間的“中邊”可以組成任何三角形，如果定義中邊必須等於長邊和短邊的均值，那么就定義了一類在金融市場圖形技術上有用處的均值中邊三角形。
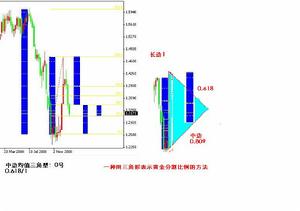均值中邊三角形示範圖定義和細節
均值中邊三角形的定義是中邊的兩倍值等於長邊加短邊，這個值可以在梯形面積公式和等差級數中找到數學根據，同時符合抽象賦范或距離空間的"模//范"的抽象定義。
如果邊長為0.382, 0.618,1,1.618,2,2.618等那么可以定義金融市場圖表（股票行情圖）比例的編號三角形：
0號均值中邊三角形：短邊為 0.618，長邊為1，而中邊為（1+0.618）/2=0.809。
-1號均值中邊三角形：短邊為 0.382，長邊為1，而中邊為（1+0.382）/2=0.691。
+1號均值中邊三角形：短邊為 0.618，長邊為1.618，而中邊為（0.618+2.618）/2=1.118。
其中可以將中邊忽略，而只記下一些黃金分割比例作簡記表示：
0號三角的簡記：0.618/1;
-1號三角的簡記：0.382/1;
+1號三角的簡記：0.618/1.618=0.382;
所以-2號三角的簡記：0.236/1;原因是：0.382/1.618=0.236; 也正因為0.618/2.618=0.236,所以
+2號三角的簡記：0.618/2.618。
其中0號均值中邊三角形可以按上文圖例的均值中邊三角形示範圖來作出。
參考：
0號均值中邊三角形，三角形，
黃金分割，0.618
