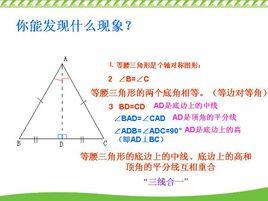
證明方法
 等邊對等角證明
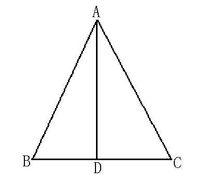
等邊對等角證明如圖,在△ABC中,AB=AC,求證:∠B=∠C。
證法1
證明:
作AD平分∠BAC
∴∠BAD=∠CAD(角平分線定義)
在△ABD與△ACD中:
AB=AC(已知)
∠BAD=∠CAD(已證)
AD=AD(公共邊)
∴△ABD≌△ACD(SAS)
∴∠B=∠C(全等三角形的對應角相等)
證法2
證明:
作AD⊥BC於D
∴∠ADB=∠ADC=90度
∴在Rt△ABD與Rt△ACD中:
AB=AC(已知)
AD=AD(公共邊)
∴Rt△ABD≌Rt△ACD(HL)
∴∠B=∠C(全等三角形的對應角相等)
證法3
證明:
作△ABC中線AD交BC於點D
∵AD是BC中線,
∴BD=CD
在△ABD與△ACD中:
AD=AD(公共邊)
AC=AB(已知)
BD=CD(已知)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形的對應角相等)
證法4
證明:
在△ABC和△ACB中:
AB=AC(已知)
BC=CB(公共邊)
AC=AB(已知)
∴△ABC≌△ACB(SSS)
∴∠B=∠C(全等三角形的對應角相等)
正弦定理
∵AB=AC,AB/sinC=AC/sinB
∴sinB=sinC
∴B=C或B+C=180°
∵AB交AC於A
∴B+C≠180°
∴B=C
餘弦定理
cosB=(AB²+BC²-AC²)/(2*AB*BC)
cosC=(AC²+BC²-AB²)/(2*AC*BC)
∵AB=BC
∴兩式相減,化簡得cosB=cosC
∴B=C