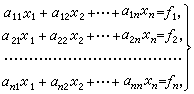基本內容
利用消元法解題的常用方法和技巧有:
1代入消元法;
2加減消元法;
3整體消元法;
4換元消元法;
5構造消元法;
6因式分解消元法;
7常數消元法;
8利用比例性質消元法;
9無腦暴力消元法
代入消元法是將方程組中的一個方程的未知數用含有另一個未知數的代數式表示,並代入到另一個方程中去,這就消去了一個未知數,得到一個解。代入消元法簡稱代入法。
代入消元法解二元一次方程的一般步驟 用代入消元法解二元一次方程組的步驟:
(1)從方程組中選取一個係數比較簡單的方程,把其中的某一個未知數用含另一個未知數的式子表示出來。
(2)把(1)中所得的方程代入另一個方程,消去一個未知數。
(3)解所得到的一元一次方程,求得一個未知數的值。
(4)把所求得的一個未知數的值代入(1)中求得的方程,求出另一個未知數的值,從而確定方程組的解。
代入消元法
方法
把其中一個方程的某個未知數的個數變成1,代入另一個方程即可。比如:
2x+y=9 ① y=x+2 ①
5x+3y=21② 2x-y=-1 ②
解:由①得:y=9-2x ③
把①代入②得:2x-(x+2)=-1
把③代入②得:5x+3(9-2x)=21
2x-x-2=-1
5x+27-6x =21 2x- x=-1+2
5x-6x = 21-27 x=1
-x = -6
把x=1代入①得:
y=3
x =6
∴方程組的解為
x=6
把x=6代入③得:
y=3
∴方程組的解為
x=6
y=-3
例子
{x-y=3 ①
{3x-8y=4②
由①得x=y+3③
③代入②得
3(y+3)-8y=4
y=1
所以x=4
則:這個二元一次方程組的解
{x=4
{y=1
強行消元法
將式子完全拆開,再將各項進行因式分解並消元。此方法計算量較大,適用於較複雜的消元。