相關內容
 高等數學
高等數學初等數學研究的是常量與勻變數,高等數學研究的是非勻變數。高等數學(它是幾門課程的總稱)是理、工科院校一門重要的基礎學科,也是非數學專業理工科專業學生的必修數學課,也是其它某些專業的必修課。
作為一門基礎科學,高等數學有其固有的特點,這就是高度的抽象性、嚴密的邏輯性和廣泛的套用性。抽象性和計算性是數學最基本、最顯著的特點,有了高度抽象和統一,我們才能深入地揭示其本質規律,才能使之得到更廣泛的套用。嚴密的邏輯性是指在數學理論的歸納和整理中,無論是概念和表述,還是判斷和推理,都要運用邏輯的規則,遵循思維的規律。所以說,數學也是一種思想方法,學習數學的過程就是思維訓練的過程。人類社會的進步,與數學這門科學的廣泛套用是分不開的。尤其是到了現代,電子計算機的出現和普及使得數學的套用領域更加拓寬,現代數學正成為科技發展的強大動力,同時也廣泛和深入地滲透到了社會科學領域。
簡介
 梯度
梯度初等數學研究的是常量和勻變數,高等數學研究的是勻變數變數。常見的“高等數學”課本通常有這樣一些內容:微積分,高等代數,機率論與數理統計。理工科(數學專業在外)的,深一些;文科的,淺一些。理工科的不同專業,文科的不同專業,深淺程度又各不相同。研究變數的是高等數學。可高等數學並不只研究變數。
高等數學是高等學校工科本科有關專業學生的一門必修的重要基礎課。通過這門課程的學習,使學生獲得向量代數與空間解析幾何、微積分的基本知識,必要的基礎理論和常用的運算方法,並注意培養學生的運算能力和初步的抽象思維、邏輯推理及空間想像能力,從而使學生獲得解決實際問題能力的初步訓練,為學習後繼課程奠定必要的數學基礎。
高等數學(也稱為微積分)是理、工科院校一門重要的基礎學科。作為一門科學,高等數學有其固有的特點,這就是高度的抽象性、嚴密的邏輯性,複雜的計算性和廣泛的套用性。抽象性是數學最基本、最顯著的特點--有了高度抽象和統一,我們才能深入地揭示其本質規律,才能使之得到更廣泛的套用。嚴密的邏輯性是指在數學理論的歸納和整理中,無論是概念和表述,還是判斷和推理,都要運用邏輯的規則,遵循思維的規律。複雜的計算性是高等數學有繁多的計算對象,眾多的定理,多樣的計算和證明方法,實際套用中複雜的計算量。所以說,數學也是一種思想方法,學習數學的過程就是思維訓練的過程。人類社會的進步,與數學這門科學的廣泛套用是分不開的。尤其是到了現代,電子計算機的出現和普及使得數學的套用領域更加拓寬,現代數學正成為科技發展的強大動力,同時也廣泛和深入地滲透到了社會科學領域。因此,學好高等數學對我們來說相當重要。然而,很多學生對怎樣才能學好這門課程感到困惑。
學習要領
首先,理解概念。數學中有很多概念。概念反映的是事物的本質,弄清楚了它是如何定義的、有什麼性質,才能真正地理解一個概念。
其次,掌握定理。定理是一個正確的命題,分為條件和結論兩部分。對於定理除了要掌握它的條件和結論以外,還要搞清它的適用範圍,做到有的放矢。
第三,在弄懂例題的基礎上作適量的習題。要特別提醒學習者的是,課本上的例題都是很典型的,有助於理解概念和掌握定理,要注意不同例題的特點和解法法在理解例題的基礎上作適量的習題。作題時要善於總結----不僅總結方法,也要總結錯誤。這樣,作完之後才會有所收穫,才能舉一反三。
第四,理清脈絡。要對所學的知識有個整體的把握,及時總結知識體系,這樣不僅可以加深對知識的理解,還會對進一步的學習有所幫助。
高等數學中包括微積分和立體解析幾何,級數和常微分方程。其中尤以微積分的內容最為系統且在其他課程中有廣泛的套用.微積分的理論是由牛頓和萊布尼茨完成的.(當然在他們之前就已有微積分的套用,但不夠系統)無窮小和極限的概念微積分的基本概念但理解有很大難度。高等數學有兩個特點:1.等價代換。在極限類的計算里,常等價代換一些因子(這在量的計算中是不可理解),但極限是階的計算。2.如果原函式形式使計算很困難,可使用原函式的積分或微分形式,這是化簡計算的思想。這三個函式之間的關係就是微分方程。
歷史發展
一般認為,16世紀以前發展起來的各個數學學科總的是屬於初等數學的範疇,因而,17世紀以後建立的數學學科基本上都是高等數學的內容。由此可見,高等數學的範疇無法用簡單的幾句話或列舉其所含分支學科來說明。19世紀以前確立的幾何、代數、分析三大數學分支中,前兩個都原是初等數學的分支,其後又發展了屬於高等數學的部分,而只有分析從一開始就屬於高等數學。分析的基礎——微積分被認為是“變數的數學”的開始,因此,研究變數是高等數學的特徵之一。原始的變數概念是物質世界變化的諸量的直接抽象,現代數學中變數的概念包含了更高層次的抽象。如數學分析中研究的限於實變數,而其他數學分支所研究的還有取複數值的復變數和向量、張量形式的,以及各種幾何量、代數量,還有取值具有偶然性的隨機變數、模糊變數和變化的(機率)空間——範疇和隨機過程。描述變數間依賴關係的概念由函式發展到泛函、變換以至於函子。與初等數學一樣,高等數學也研究空間形式,只不過它具有更高層次的抽象性,並反映變化的特徵,或者說是在變化中研究它。例如,曲線、曲面的概念已發展成一般的流形。按照埃爾朗根綱領,幾何是關於圖形在某種變換群下不變性質的理論,這也就是說,幾何是將各種空間形式置於變換之下來來研究的。
無窮進入數學,這是高等數學的又一特徵。現實世界的各種事物都以有限的形式出現,無窮是對他們的共同本質的一種概括。所以,無窮進入數學是數學高度理論化、抽象化的反映。數學中的無窮以潛無窮和實無窮兩種形式出現。在極限過程中,變數的變化是無止境的,屬於潛無窮的形式。而極限值的存在又反映了實無窮過程。最基本的極限過程是數列和函式的極限。數學分析以它為基礎,建立了刻畫函式局部和總體特徵的各種概念和有關理論,初步成功地描述了現實世界中的非均勻變化和運動。另外一些形式上更為抽象的極限過程,在別的數學學科中也都起著基本的作用。還有許多學科的研究對象本身就是無窮多的個體,也就說是無窮集合,例如群、環、域之類及各種抽象空間。這是數學中的實無窮。能夠處理這類無窮集合,是數學水平與能力提高的表現。為了處理這類無窮集合,數學中引進了各種結構,如代數結構、序結構和拓撲結構。另外還有一種度量結構,如抽象空間中的範數、距離和測度等,它使得個體之間的關係定量化、數位化,成為數學的定性描述和定量計算兩方面的橋樑。上述結構使得這些無窮集合具有豐富的內涵,能夠彼此區分,並由此形成了眾多的數學學科。
數學的計算性方面。在初等數學中甚至占了主導的地位。它在高等數學中的地位也是明顯的,高等數學除了有很多理論性很強的學科之外,也有一大批計算性很強的學科,如微分方程、計算數學、統計學等。在高度抽象的理論裝備下,這些學科才有可能處理現代科學技術中的複雜計算問題。
除了數學基礎、集合論、數理邏輯這樣一些基礎性學科之外,數學分為初等數學與高等數學兩大部分。它們有共同的基礎,而彼此之間並沒有嚴格的界限。它們都是人類文明在不同發展階段的產物,但並不像某些事物那樣,後發展起來的可以代替古老的,隨著人類文明的進步,數學中某些局部的、繁瑣的成果或工作可能被淘汰,而其總體仍然是有用的,並必將向著更加綜合和抽象、結構更多樣化的方向發展下去。
分類
一、函式極限連續
二、一元函式微分學
三、一元函式積分學
四、向量代數與空間解析幾何
五、多元函式微分學
六、多元函式積分學
七、無窮級數
八、常微分方程
主要包括
一、函式與極限分為
常量與變數
函式
函式的簡單性態
反函式
初等函式
數列的極限
函式的極限
無窮大量與無窮小量
無窮小量的比較
函式連續性
連續函式的性質及初等函式函式連續性
二、導數與微分
導數的概念
函式的和、差求導法則
函式的積、商求導法則
複合函式求導法則
反函式求導法則
高階導數
隱函式及其求導法則
函式的微分
三、導數的套用
微分中值定理
未定式問題
函式單調性的判定法
函式的極值及其求法
函式的最大、最小值及其套用
曲線的凹向與拐點
四、不定積分
不定積分的概念及性質
求不定積分的方法
幾種特殊函式的積分舉例
五、定積分及其套用
定積分的概念
微積分的積分公式
定積分的換元法與分部積分法
廣義積分
六、空間解析幾何
空間直角坐標系
方向餘弦與方向數
平面與空間直線
曲面與空間曲線
七、多元函式的微分學
多元函式概念
二元函式極限及其連續性
偏導數
全微分
多元複合函式的求導法
多元函式的極值
八、多元函式積分學
二重積分的概念及性質
二重積分的計算法
三重積分的概念及其計算法
九、常微分方程
微分方程的基本概念
可分離變數的微分方程及齊次方程
線性微分方程
可降階的高階方程
線性微分方程解的結構
二階常係數齊次線性方程的解法
二階常係數非齊次線性方程的解法
十、無窮級數
導數的概念
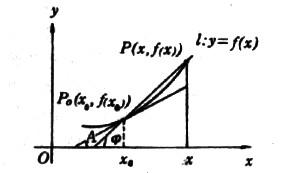 有關導數
有關導數例:設一質點沿x軸運動時,其位置x是時間t的函式,y=f(x),求質點在t0的瞬時速度?
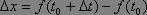 數學
數學我們知道時間從t0有增量△t時,質點的位置有增量
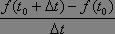 數學
數學這就是質點在時間段△t的位移。因此,在此段時間內質點的平均速度為;
若質點是勻速運動的則這就是在t0的瞬時速度,若質點是非勻速直線運動,則這還不是質點在t0時的瞬時速度。
我們認為當時間段△t無限地接近於0時,此平均速度會無限地接近於質點t0時的瞬時速度,
即:質點在t0時的瞬時速度=
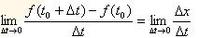 數學
數學為此就產生了導數的定義,如下:
導數的定義
設函式y=f(x)在點x0的某一鄰域內有定義,當自變數x在x0處有增量△x(x+△x也在該鄰域內)時,相應地
函式有增量
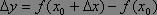 數學
數學若△y與△x之比當△x→0時極限存在,則稱這個極限值為y=f(x)在x0處的導數。
記為:
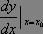 數學
數學還可記為:
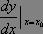 數學
數學函式f(x)在點x0處存在導數簡稱函式f(x)在點x0處可導,否則不可導。
若函式f(x)在區間(a,b)內每一點都可導,就稱函式f(x)在區間(a,b)內可導。這時函式y=f(x)對於區
間(a,b)內的每一個確定的x值,都對應著一個確定的導數,這就構成一個新的函式,
我們就稱這個函式為原來函式y=f(x)的導函式。
註:導數也就是差商的極限
左、右導數
前面我們有了左、右極限的概念,導數是差商的極限,因此我們可以給出左、右導數的概念。
若極限
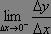 數學
數學存在,我們就稱它為函式y=f(x)在x=x0處的左導數。
若極限
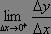 數學
數學存在,我們就稱它為函式y=f(x)在x=x0處的右導數。
註:函式y=f(x)在x0處的左右導數存在且相等是函式y=f(x)在x0處的可導的充分必要條件

