簡介
1起源
機率論機率論的起源與賭博問題有關。16世紀，義大利的學者吉羅拉莫·卡爾達諾（GirolamoCardano，1501——1576）開始研究擲骰子等賭博中的一些簡單問題。17世紀中葉，有人對博弈中的一些問題發生爭論，其中的一個問題是“賭金分配問題”，他們決定請教法國數學家帕斯卡（Pascal)和費馬（Fermat）基於排列組合方法，研究了一些較複雜的賭博問題，他們解決了分賭注問題、賭徒輸光問題。他們對這個問題進行了認真的討論，花費了3年的思考，並最終解決了這個問題，這個問題的解決直接推動了機率論的產生。
隨著18、19世紀科學的發展，人們注意到在某些生物、物理和社會現象與機會遊戲之間有某種相似性，從而由機會遊戲起源的機率論被套用到這些領域中；同時這也大大推動了機率論本身的發展。使機率論成為數學的一個分支的奠基人是瑞士數學家j.伯努利，他建立了機率論中第一個極限定理，即伯努利大數定律，闡明了事件的頻率穩定於它的機率。隨後a.de棣莫弗和p.s.拉普拉斯又導出了第二個基本極限定理（中心極限定理）的原始形式。拉普拉斯在系統總結前人工作的基礎上寫出了《分析的機率理論》，明確給出了機率的古典定義，並在機率論中引入了更有力的分析工具，將機率論推向一個新的發展階段。19世紀末，俄國數學家P.L.切比雪夫、a.a.馬爾可夫、a.m.李亞普諾夫等人用分析方法建立了大數定律及中心極限定理的一般形式，科學地解釋了為什麼實際中遇到的許多隨機變數近似服從常態分配。20世紀初受物理學的刺激，人們開始研究隨機過程。這方面a·n·柯爾莫哥洛夫、n.維納、a·a·馬爾可夫、a·r·辛欽、p·萊維及w·費勒等人作了傑出的貢獻。
1如何定義機率，如何把機率論建立在嚴格的邏輯基礎上，是機率理論發展的困難所在，對這一問題的探索一直持續了3個世紀。20世紀初完成的勒貝格測度與積分理論及隨後發展的抽象測度和積分理論，為機率公理體系的建立奠定了基礎。在這種背景下，蘇聯數學家柯爾莫哥洛夫1933年在他的《機率論基礎》一書中第一次給出了機率的測度論的定義和一套嚴密的公理體系。他的公理化方法成為現代機率論的基礎，使機率論成為嚴謹的數學分支，對機率論的迅速發展起了積極的作用。
機率與統計的一些概念和簡單的方法，早期主要用於賭博和人口統計模型。隨著人類的社會實踐，人們需要了解各種不確定現象中隱含的必然規律性，並用數學方法研究各種結果出現的可能性大小，從而產生了機率論，並使之逐步發展成一門嚴謹的學科。現在，機率與統計的方法日益滲透到各個領域，並廣泛套用於自然科學、經濟學、醫學、金融保險甚至人文科學中。
數學家和精算師認為機率是在0至1之間之閉區間的數字，指定給一發生與失敗是隨機的“事件”。機率P(A)根據機率公理來指定給事件A。一事件A在一事件B確定發生後會發生的機率稱為B給之A的條件機率；其數值為
機率
機率作為數學統計基礎的機率論的創始人分別是法國數學家帕斯卡和費馬，其可追溯到公元17世紀。當時的法國宮廷貴族裡盛行著擲骰子遊戲，遊戲規則是玩家連續擲4次骰子，如果其中沒有6點出現，玩家贏，如果出現一次6點，則莊家（相當於現在的賭場）贏。按照這一遊戲規則，從長期來看，莊家扮演贏家的角色，而玩家大部分時間是輸家，因為莊家總是要靠此為生的，因此當時人們也就接受了這種現象。
後來為了使遊戲更刺激，遊戲規則發生了些許變化，玩家這回用2個骰子連續擲24次，不同時出現2個6點，玩家贏，否則莊家贏。當時人們普遍認為，2次出現6點的機率是一次出現6點的機率的1/6，因此6倍於前一種規則的次數，也既是24次贏或輸的機率與以前是相等的。然而事實卻剛好相反，從長期來看，這回莊家處於輸家的狀態，於是他們去請教當時的數學家帕斯卡，求助其對這種現象作出解釋。
1其他對機率論的發展作出重要貢獻的人還有荷蘭物理、數學家惠更斯，瑞士物理、數學家伯努利，法國數學家美弗，法國數學、天文學家拉普拉斯，德國數學家高斯，法國物理、數學家泊松，義大利數學、醫學家卡爾達諾以及蘇聯數學家柯爾莫哥洛夫。
相關事例
機率論1.六合彩：在六合彩（49選6）中，一共有13983816種可能性（參閱組合數學），普遍認為，如果每周都買一個不相同的號，最晚可以在13983816/52（周）=268919年後獲得頭等獎。事實上這種理解是錯誤的，因為每次中獎的機率是相等的，中獎的可能性並不會因為時間的推移而變大。
2.生日悖論：在一個足球場上有23個人（2×11個運動員和1個裁判員），不可思議的是，在這23人當中至少有兩個人的生日是在同一天的機率要大於50％。
3.輪盤遊戲：在遊戲中玩家普遍認為，在連續出現多次紅色後，出現黑色的機率會越來越大。這種判斷也是錯誤的，即出現黑色的機率每次是相等的，因為球本身並沒有“記憶”，它不會意識到以前都發生了什麼，其機率始終是18/37。
4.輪盤：在電視台舉辦的猜隱藏在門後面的汽車的遊戲節目中，在參賽者的對面有三扇關閉的門，其中只有一扇門的後面有一輛汽車，其它兩扇門後是山羊。遊戲規則是，參賽者先選擇一扇他認為其後面有汽車的門，但是這扇門仍保持關閉狀態，緊接著主持人打開沒有被參賽者選擇的另外兩扇門中後面有山羊的一扇門，這時主持人問參賽者，要不要改變主意，選擇另一扇門，以使得贏得汽車的機率更大一些？正確結果是，如果此時參賽者改變主意而選擇另一扇關閉著的門，他贏得汽車的機率會增加一倍。
事件
單位事件、事件空間、隨機事件
在一次隨機試驗中可能發生的唯一的，且相互之間獨立的結果被成為單位事件，用e表示。在隨機試驗中可能發生的所有單位事件的集合稱為事件空間，用S來表示。例如在一次擲骰子的隨機試驗中，如果用獲得的點數來表示單位事件，那么一共可能出現6個單位事件，則事件空間可以表示為S={1，2，3，4，5，6}。
上面的事件空間是由可數有限單位事件組成，事實上還存在著由可數無限以及不可數單位事件組成的事件空間，比如在一次直到獲得國徽面朝上的隨機擲硬幣試驗中，其事件空間由可數無限單位事件組成，表示為：S={國，數國，數數國，數數數國，數數數數國，···}，注意到在這個例子中"數數數國"是單位事件。將兩根筷子隨意扔向桌面，其靜止後所形成的交角假設為α，這個隨機試驗的事件空間的組成可以表示為S={α|0≤α<180}。
隨機事件是事件空間S的子集，它由事件空間S中的單位元素構成，用大寫字母A，B，C...表示。例如在擲兩個骰子的隨機試驗中，設隨機事件A="獲得的點數和大於10"，則A可以由下面3個單位事件組成：A={(5，6)，(6，5)，(6，6)}。
如果在隨機試驗中事件空間中的所有可能的單位事件都發生，這個事件被稱為必然事件，表示為S⊂S；相應的如果事件空間裡不包含任何一個單位事件，則稱之為不可能事件，表示為∅⊂S。
事件的計算
因為事件在一定程度上是以集合的含義定義的，因此可以把集合計算方法直接套用於事件的計算，也就是說，在計算過程中，可以把事件當作集合來對待。
 |  |  |
| A的補集 不屬於A的事件發生 | 聯集A∪B 或者A或者B或者A，B同時發生 | 交集A∩B 事件A，B同時發生 |
 |  |  |
| 差集A\B 不屬於B的A事件發生 | 空集A∩B=∅ A，B事件不同時發生 | 子集B⊆A 如B發生，則A也一定發生 |
機率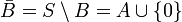
機率
機率在輪盤遊戲中假設A代表事件“球落在紅色區域”，B代表事件"球落在黑色區域"，因為事件A和B沒有共同的單位事件，因此可表示為
注意到事件A和B並不是互補的關係，因為在整個事件空間S中還有一個單位事件“零”，其即不是紅色也不是黑色，而是綠色，因此A，B的補集應該分別表示如下：
機率的定義
傳統機率(拉普拉斯機率)
機率傳統機率的定義是由法國數學家拉普拉斯(Laplace)提出的。如果一個隨機試驗所包含的單位事件是有限的，且每個單位事件發生的可能性均相等，則這個隨機試驗叫做拉普拉斯試驗。在拉普拉斯試驗中，事件A在事件空間S中的機率P(A)為：
例如，在一次同時擲一個硬幣和一個骰子的隨機試驗中，假設事件A為獲得國徽面且點數大於4，那么事件A的機率應該有如下計算方法：S={(國徽，1點)，(數字，1點)，(國徽，2點)，(數字，2點)，(國徽，3點)，(數字，3點)，(國徽，4點)，(數字，4點)，(國徽，5點)，(數字，5點)，(國徽，6點)，(數字，6點)}，A＝{(國徽，5點)，(國徽，6點)}，按照拉普拉斯定義，A的機率為，
機率注意到在拉普拉斯試驗中存在著若干的疑問，在現實中是否存在著這樣一個試驗，其單位事件的機率具有精確的相同的機率值，因為人們不知道，硬幣以及骰子是否"完美"，即骰子製造的是否均勻，其重心是否位於正中心，以及輪盤是否傾向於某一個數字。儘管如此，傳統機率在實踐中被廣泛套用於確定事件的機率值，其理論根據是：如果沒有足夠的論據來證明一個事件的機率大於另一個事件的機率，那么可以認為這兩個事件的機率值相等。
如果仔細觀察這個定義會發現拉普拉斯用機率解釋了機率，定義中用了"相同的可能性"(原文是égalementpossible)一詞，其實指的就是"相同的機率"。這個定義也並沒有說出，到底什麼是機率，以及如何用數字來確定機率。在現實生活中也有一系列問題，無論如何不能用傳統機率定義來解釋，比如，人壽保險公司無法確定一個50歲的人在下一年將死去的機率等。
統計機率
統計機率是建立在頻率理論基礎上的，分別由英國邏輯學家約翰(JohnVenn1834-1923)和奧地利數學家理察(RichardVonMises1883-1953)提出，他們認為，獲得一個事件的機率值的唯一方法是通過對該事件進行100次，1000次或者甚至10000次的前後相互獨立的n次隨機試驗，針對每次試驗均記錄下絕對頻率值和相對頻率值hn(A)，隨著試驗次數n的增加，會出現如下事實，即相對頻率值會趨於穩定，它在一個特定的值上下浮動，也即是說存在著一個極限值P(A)，相對頻率值趨向於這個極限值。這個極限值被稱為統計機率，表示為：
機率例如，若想知道在一次擲骰子的隨機試驗中獲得6點的機率值可以對其進行3000次前後獨立的扔擲試驗，在每一次試驗後記錄下出現6點的次數，然後通過計算相對頻率值可以得到趨向於某一個數的統計機率值。
| 扔擲數 | 獲得6點的絕對頻率 | 獲得6點的相對頻率 |
| 1 | 1 | 1.00000 |
| 2 | 1 | 0.50000 |
| 3 | 1 | 0.33333 |
| 4 | 1 | 0.25000 |
| 5 | 2 | 0.40000 |
| 10 | 2 | 0.20000 |
| 20 | 5 | 0.25000 |
| 100 | 12 | 0.12000 |
| 200 | 39 | 0.19500 |
| 300 | 46 | 0.15333 |
| 400 | 72 | 0.18000 |
| 500 | 76 | 0.15200 |
| 600 | 102 | 0.17000 |
| 700 | 120 | 0.17143 |
| 1000 | 170 | 0.17000 |
| 2000 | 343 | 0.17150 |
| 3000 | 560 | 0.16867 |
上面提到的這個有關相對頻率的經驗值又被稱為大數定律，是頻率理論學家定義機率論的基礎。然而沒有人可以將骰子無限的扔下去，因此在實踐中也就無法有力的證明大數定律，許多來自數學理論的論證至今也沒有取得成功。儘管如此，統計機率在今天的實踐中具有重要意義，它是數理統計的基礎。
機率公理
機率
機率如果一個函式P指定給每一個事件空間S中的事件A一個實數P(A)，並且其滿足下面的3個公理，那么函式P叫做機率函式，相應的P(A)叫做事件A的機率。
公理1： 事件A的機率P(A)是一個非負實數。 公理2： 完全事件的機率值為1。 公理3： 空集事件的加法法則。 |
，如果
不難看出，上述公理適用於包括拉普拉斯機率和統計機率在內的所有機率定義。如果若干事件間的關係是兩兩空集，那么公理3還可以擴展為如下形式：
機率公理3：
計算
需要提及的是下面將要介紹的9個計算機率的定理與上面已經提及的事件的計算沒有關係，所有關於機率的定理均由機率的3個公理得來，同時適用於包括拉普拉斯機率和統計機率在內的所有機率理論。
機率定理1(互補法則)
機率與A互補事件的機率始終是
機率論事件A和Ā是互補關係，由公理3和公理2可得
機率
機率利用互補法則，可以解決下面這個問題，在兩次連續鏇轉的輪盤遊戲中，至少有一次是紅色的機率是多少？
第一次鏇轉紅色不出現的機率是19/37，按照乘法法則，第二次也不出現紅色的機率是(19/37)2=0.2637，因此在這裡互補機率就是指在兩次連續鏇轉中至少有一次是紅色的機率，
機率定理2
不可能事件的機率為零：
機率證明：
ø和S是互補事件，按照公理2有
P(S)=1，再根據上面的定理1得到
機率定理3
如果若干事件A1，A2，...An∈S每兩兩之間是空集關係，那么這些所有事件集合的機率等於單個事件的機率的和。
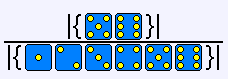
機率注意針對這一定理有效性的決定因素是A1...An事件不能同時發生。例如，在一次擲骰子中，得到5點或者6點的機率是：
P=P(A5)+P(A6)=
機率
機率
機率定理4
如果事件A，B是差集關係，則有，
機率證明：
機率論
機率和
機率由公理3得，
機率定理5(任意事件加法法則)
對於事件空間S中的任意兩個事件A和B，有如下定理：
機率證明：
事件A∪B由下面三個事件組成：
機率首先根據定理4有：
機率
機率再根據定理3得：
機率
機率
機率例如，在由一共32張牌構成的斯卡特撲克牌中隨機抽出一張，其或者是"方片"或者是"
機率事件A，B是或者的關係，且可同時發生，就是說抽出的這張牌即可以是"方片"，又可以是"
機率
機率從圖片上也可看出，符合這一條件的恰好是11張牌。注意到定理3是定理5的特殊情況，即A，B不同時發生，相應的P(A∩B)=0。
定理6(乘法法則)
事件A，B同時發生的機率是：
機率
輪盤遊戲示意圖 
機率或者，
機率從上面的圖中也可以看出，符合條件的只有一張牌，即方片A。
另一個例子，在32張斯卡特牌里連續抽兩張(第一次抽出的牌不放回去)，連續得到兩個A的機率是多少呢？
設A，B分別為連續發生的這兩次事件，人們看到，A，B之間有一定聯繫，即B的機率由於A發生了變化，屬於條件機率，按照公式有：
機率定理7(無關事件乘法法則)
兩個不相關聯的事件A，B同時發生的機率是：
機率注意到這個定理實際上是定理6(乘法法則)的特殊情況，如果事件A，B沒有聯繫，則有P(A|B)=P(A)，以及P(B|A)=P(B)。現在觀察一下輪盤遊戲中兩次連續的鏇轉過程，P(A)代表第一次出現紅色的機率，P(B)代表第二次出現紅色的機率，可以看出，A與B沒有關聯，利用上面提到的公式，連續兩次出現紅色的機率為：
機率忽視這一定理是造成許多玩家失敗的根源，普遍認為，經過連續出現若干次紅色後，黑色出現的機率會越來越大，事實上兩種顏色每次出現的機率是相等的，之前出現的紅色與之後出現的黑色之間沒有任何聯繫，因為球本身並沒有"記憶"，它並不"知道"以前都發生了什麼。同理，連續10次出現紅色的機率為P=(18/37)10=0.0007
完全機率
n個事件H1，H2，...Hn互相間獨立，且共同組成整個事件空間S，即
機率，
機率
機率這時A的機率可以表示為，
機率證明：
機率按照公理3，有
機率根據乘法法則，
機率因此有，
機率
機率例如，一個隨機試驗工具由一個骰子和一個柜子中的三個抽屜組成，抽屜1里有14個白球和6個黑球，抽屜2里有2個白球和8個黑球，抽屜3里有3個白球和7個黑球，試驗規則是首先擲骰子，如果獲得小於4點，則抽屜1被選擇，如果獲得4點或者5點，則抽屜2被選擇，其他情況選擇抽屜3。然後在選擇的抽屜里隨機抽出一個球，最後抽出的這個球是白球的機率是：
P(白)=P(白|抽1)·P(抽1)+P(白|抽2)·P(抽2)＋P(白|抽3)·P(抽3)
=(14/20)·(3/6)+(2/10)·(2/6)+(3/10)·(1/6)
=28/60=0.4667
從例子中可看出，完全機率特別適合於分析具有多層結構的隨機試驗的情況。
貝葉斯定理
貝葉斯定理由英國數學家貝葉斯(ThomasBayes1702-1761)發展，用來描述兩個條件機率之間的關係，比如P(A|B)和P(B|A)。按照定理6的乘法法則，P(A∩B)=P(A)·P(B|A)=P(B)·P(A|B)，可以立刻導出貝葉斯定理：
機率如上公式也可變形為
機率例如：一座別墅在過去的20年裡一共發生過2次被盜，別墅的主人有一條狗，狗平均每周晚上叫3次，在盜賊入侵時狗叫的機率被估計為0.9，問題是：在狗叫的時候發生入侵的機率是多少？
人們假設A事件為狗在晚上叫，B為盜賊入侵，則P(A)=3/7，P(B)=2/(20·365)=2/7300，P(A|B)=0.9，按照公式很容易得出結果：
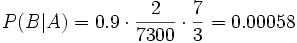機率另一個例子，現分別有A，B兩個容器，在容器A里分別有7個紅球和3個白球，在容器B里有1個紅球和9個白球，現已知從這兩個容器里任意抽出了一個球，且是紅球，問這個紅球是來自容器A的機率是多少?
假設已經抽出紅球為事件B，從容器A里抽出球為事件A，則有：P(B)=8/20，P(A)=1/2，P(B|A)=7/10，按照公式，則有：
機率套用
雖然機率論最早產生於17世紀，然而其公理體系只在20世紀的20至30年代才建立起來並得到迅速發展，在過去的半個世紀裡機率論在越來越多的新興領域顯示了它的套用性和實用性，例如：物理、化學、生物、醫學、心理學、社會學、政治學、教育學，經濟學以及幾乎所有的工程學等領域。特別值得一提的是，機率論是今天數理統計的基礎，其結果被用做問卷調查的分析資料或者對經濟前景進行預測。
