定義
做變速運動的物體其位移與時間的比值不是恆定不變的,這時我們可以用一個速度粗略地描述物體在這段時間內的運動的快慢情況,這個速度就叫做平均速度。
公式
定義式
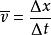 平均速度
平均速度(△x=位移 △t=通過這段位移所用的時間)
其它計算公式
2×V1×V2÷(V1+V2)=平均速度。(前半路程平均速度V1,後半路程平均速度V2)
在勻變速直線運動中,平均速度還可以用(V0+Vt)÷2 來計出,此時平均速度還表示通過這段位移所用的時間的中間時刻的瞬時速度。
但如果是勻變速運動,那么還有一種公式=(初速度+末速度)/2
概念
(1)反映一段時間內物體運動的平均快慢程度,它與一段位移或一段時間相對應。
(2)在變速直線運動中,平均速度的大小與選定的時間或位移有關,不同時間段內或不同位移上的平均速度一般不同,必須指明求出的平均速度是對應哪段時間內或哪段位移的平均速度,不指明對應的過程的平均速度是沒有意義的。
(3)平均速度是矢量,其方向與一段時間Δt內發生的位移方向相同,與運動方向不一定相同。
(4)在勻變速直線運動中,中間位置的瞬時速度大於中間時刻的瞬時速度。
推導:
中間時刻Vp,中間位移Vs
Vp=Vo+at}
Vt=Vp+at}Vp=Vo+Vt/2=平均速度
Vs2—Vo2=2a_s=X}
Vt2—Vs2=2a_S=X}Vs2—Vo2=Vt2—Vs2
2Vs2=Vt2+Vo2
∴Vs=√[Vt2+Vo2]/2
又∵中間位置的速度是算術平均,中間時刻的速度是平方平均,由均值不等式可知,∴中間位置的瞬時速度都要大於中間時刻的瞬時速度。
區別
平均速度與平均速率的區別
平均速率不是平均速度。平均速率是物體通過路程與它通過這段路程所用的時間的比值,它是標量。
(當是單方向直線運動時,平均速度在數值上等於平均速率。)
平均速率是路程與時間之比值,比值不能衡量,一般情況下不等於平均速度的大小。
例如一個物體圍繞一個圓周運動一周,花的時間是t,平均速率是2πr/t,而平均速度為0。
具體的說,平均速度指的是你所選定的時間內物體位移的速度,而在上面的例子中,t秒後此物體已返回原地,所以它的位移為零,平均速度大小亦為零。

