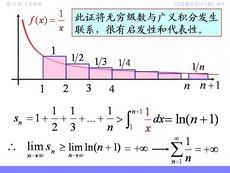
函式
如果級數的每一項依賴於一個連續變數x,un=un(x),x在一個區間α≤x ≤b上變化,這個級數就成為一個函式項級數,簡稱函式級數,記為
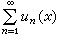 公式9
公式9這裡x的值自然被分成兩類C和D,使得當x屬於C時級數收斂,當x屬於D時級數發散。幾何級數∑rn事實上就是一個函式級數,它的收斂範圍是一個區間(-1<1)。微分學裡的泰勒級數代表著一類函式級數,形如
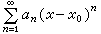 公式10
公式10稱為冪級數。這種級數,作為幾何級數的一種推廣,其收斂範圍C仍然是一個區間(以x=x0為中心,帶或不帶端點,有限或無限,或退化成一點)。這種級數,當x換成復變數z之後,成為研究複變函數的一個基本工具(見複變函數論)。積分學裡的傅立葉級數代表著另一類函式級數,形如
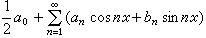 公式11
公式11稱為三角級數。這種級數是研究實變函式的一個重要工具,它們的收斂範圍一般很複雜,對它們的研究促使了G.(F.P.)康托爾創建集合的基礎理論(見實變函式論、傅立葉分析)。
一般說來,一個函式級數的和函式,作為一個無限項的和,不是在它的整個收斂集C上,而是只在C的某種帶有限制的部分C1上,才像一個有限項的和。下面試從C的某一點x出發來看級數(15)的收斂性。這級數在這一點x處收斂,就是說,它的部分和sm(x)收斂到一個和數s(x),也就是說:對於任意一個正數級數都有隻要m充分大。這個不等式還可能對於C的其他一些點x也成立。如果這個不等式在C的某一部分C1上處處成立,這就意味著sm(x)這個函式在集合C 1上一致地近似於s(x)這個函式,精確度(處處)在級數以內。而如果這在C1上對於每一個正數級數都成立只要m充分大,那就意味著這一序列函式sm(x),或者就說是函式級數∑un(x)本身,在C1上一致地無限逼近於函式s(x),或者簡單地說, sn(x)一致地收斂到函式s(x)。這樣,原來的收斂概念,在與函式概念結合之後,就發展成為適合於函式級數的一種收斂概念。
一致收斂
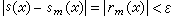 公式12
公式12一個函式級數級數說是在一個集合C1上一致地收斂到它的和函式s(x),是指對於每一個正數級數都存在一個自然數N(不依賴於x),使得當m>N 時
對於一切屬於C1的x都成立。
這時級數的和函式s(x),作為一個無限項的和,便可在整個集合C1上通過特徵性質繼承有限項和的一些分析性質。
逐項積分定理 設函式級數級數在有限閉區間α≤x≤b上一致地收斂。於是,若級數的各項都連續,則級數的和也連續並且可以逐項積分
關於逐項微分,沒有直接類似的定理(因為一致小的函式rm(x)的導數可以任意大);但是通過微分與積分的互逆關係(微積分基本定理)能夠把上述定理轉變成逐項微分的形式。
逐項微分定理
設函式級數級數在區間α
級數在逐項取絕對值之後就成為正項級數,顯然可以依一致收斂性進行比較,特別是用一個常數級數進行比較,便有M判別法。 M判別法設函式級數 級數在一集合C1上受常數級數級數控制:
於是,若級數收斂,則級數在C1上一致收斂。
函式的展開
一個函式級數在其收斂範圍內代表一個函式,即它的和:當和函式未給定時,級數是定義這函式的一種方式;當和函式已給定時,級數是揭示這函式依賴於基本變數的規律的一種方式──函式的級數展開。微積分在創建的初期通過形式處理得到了許多初等函式的級數展開,最重要的有
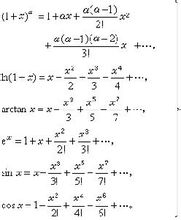 公式13
公式13但只是到了(約 200年之後)一致收斂概念明確的時候才證實,這種冪級數展開在收斂區間內可以逐項微分和積分並且收斂(區間的)半徑r不變(在前三個中 r=1,後三個中r=∞,而第一個當α 為零或正整數時化為多項式因而也有r=∞)。這時人們才嚴密地證明了,冪級數在其收斂區間內能夠完全代表它的和函式參加分析運算。於是可以逐項微分任意多次,所以這冪級數本身就是它的和函式在收斂區間中心處的泰勒級數,因而是唯一的。據此,一個泰勒級數的係數不一定要單純通過累次微分級數而可以通過某些冪級數的分析運算來求得。這就使人們能夠補充基本展開表(22)中所缺少的相當於tanx的展開,它不能像反三角函式那樣通過逐項積分得到(因為沒有現成的冪級數展開作出發點),也不能象其他基本初等函式那樣通過直接求累次微分得到(因為微分次數越多計算越複雜)。利用冪級數展開的唯一性便可嚴密地證明:
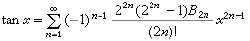 公式14
公式14式中B2n是伯努利數,確定於展開式
至於三角級數展開式的唯一性,則像它的收斂集一樣複雜,成了三角級數理論研究的一個基本問題。
函式的級數展開具有如下共同的形式:
這個形式的級數,作為冪級數的推廣,其收斂問題的分析仍舊可以利用N.H.阿貝爾在研究冪級數的收斂問題時所引進的部分求和法。
部分求和法
設級數,則有恆等式
這個方法(類似於分部積分法)立即給出:
① 級數(25)在一個集合 C1上一致收斂的一組充分條件是,級數∑αn收斂而序列vn(x)在C1上一致有界並且處處單調。
② 級數(25)在一個集合 C 1上一致收斂的一組充分條件是,級數∑αn有界而序列vn(x)在C1上一致收斂到0並且級數
在C1上一致收斂。
這兩個結果都是萊布尼茨交錯級數定理的推廣。
廣義收斂
收斂概念的近代發展。
漸近
在所考慮的問題只需注意基本變數 x充分大的情形,相當於過程x→+∞,這裡函式的級數展開就要依級數的冪來進行,而展開的意義在於每增加一項就要有一項的效果(α→0當x→+∞):
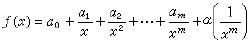 公式15
公式15m=1,2,3,…。這時,在xy坐標平面內,這一序列部分和sm(x)作為函式,其代表曲線y=sm(x)都是原來函式y=ƒ(x)的漸近線(直的或曲的),每一個比前一個更切近於曲線y=ƒ(x)。因此,採用H.龐加萊的用語就是,級數級數是一個漸近級數,漸近地代表著函式ƒ(x)。通常把這簡記為
這樣的漸近級數雖然往往是發散的,但仍可以代替它所漸近表示的函式參加四則運算,只要作為除數的級數的常數項不為0;也可以逐項微分,只要函式的導函式ƒ′(x)確實具有漸近展開;還可以逐項積分,只要把形式關係
理解為因此漸近級數可以(通過待定係數法)用於求解微分方程。當然,在原來意義下可用於近似計算,例如斯特林公式
中的級數雖是發散的卻是漸近的(式中的Bn就是式(24)中的伯努利數),只需取前幾項就能夠算得(準確到小數點後10位的)近似值:
lg(1000!)=2567.…。
發散
最早的函式的級數展開 在x=-1時給出
這個悖論式的等式在級數理論的發展過程中不時激起人們的思索。萊布尼茨認為這應從這個級數的部分和所可能取的值(1,0,1,0,…)的算術平均來理解。L.歐拉認為在涉及級數的分析研究中應堅持函式觀點:一個有限的分析表達式的(冪)級數展開應在分析運算中當作該表達式的等價物,因而級數的和就是它所由之而來的分析表達式的值。這些看法啟發了人們,對一個級數,甚至它是發散的,是否仍可以考慮它在廣義意義下的和。一般說來,就函式的級數展開的特定形式(25)而論,只要它對於充分大的x都成立而又當x→+∞時有且極限值ƒ(+∞)作為函式的邊界值是一有限數,那么就可以說係數級數 級數在依函式序列{vn(x)}的展開中可和到ƒ(+∞),以ƒ(+∞)為廣義和,並把這種邊值收斂關係簡單地記為
不過,如果要取定{vn(x)}作為一種廣義和的參考系,就應當事前適當地選取函式 vn(x)使得所產生的這種求和法是正規的,即每一個收斂級數∑αn都可和到它原有的和A。這通過阿貝爾部分求和法(26)可以用級數的部分和An表示成
這樣,這個求和法為正規的一個必要充分條件是,對x一致地有
而前提條件在這裡變成可見廣義收斂乃是級數的部分和按一種平均意義理解的收斂;所以只要極限(34)存在級數,都說級數級數在以wn(x) 為權的帶權平均的收斂過程中(平均)可和到A。
算術平均求和法(M),相當於
m=【x】為x的整數部分;切薩羅求和法(C,k),相當於
m=【x】為x的整數部分。
波萊爾還把他的求和法 (B)轉換成邊值形式並取其簡化形式如
在轉換中的誤差項級數這一前提下,(B′)與(B)等價;一般情形,只能由(B)推到(B′)。這種求和法能夠使很廣泛的一類復項冪級數∑bnzn在其收斂圓外可和,並且可以逐項積分。為了可以逐項微分,波萊爾提出了絕對可和的附加條件,即這樣一序列無窮積分都絕對收斂。
這種求和法不是正規的;只是限於絕對收斂的級數而言才是正規的。但它使冪級數的分析運算(加、減、乘、逐項微分、逐項積分等)可以在收斂圓外如同在收斂圓內一樣進行,因而很有效地擴大了冪級數的套用範圍,特別是很適合於(通過待定係數法)求解微分方程,如同漸近級數那樣。
對於兩種求和法W與W1,我們說W1比W強,意思是每一個W可和的級數都一定W1可和到相同的和,但反過來不成立。例如(B′)比(B)強,(A)比(C,k)強。這種斷定可和性強弱的定理稱為阿貝爾型定理。一個阿貝爾型定理的逆定理不成立,無非是說不能無條件地反過來,因而也就是說在適當的補充條件之下能夠反過來。說明這種補充條件的充分性定理稱為陶伯型定理。如一個阿貝爾可和的級數級數,只要級數,就必定是收斂的。
純數量上,一個(無窮)級數永遠等同於一個(無窮)積分
【x】為x的整數部分。所以級數的理論中只有基本變數n的離散性在其中根本上起著簡明性的作用的那些部分才能保持其特有的級數形式;否則遲早都會在普遍化的進程中過渡為積分的形式。例如A.普林斯海姆關於正項級數的系統研究取級數形式,而N.維納關於陶伯型定理的研究取積分形式。
發散級數求和的理論是收斂級數研究的擴展,它擴大了分析學嚴密理論的適用範圍,有效地揭示了函式的分析性質與數量關係,在傅立葉分析與函式構造論中有許多套用。
參考書目
G.H.Hardy,A Course of Pure Mathematics,10th ed.,Cambridge Univ. Press, London, 1958.
Th.J.I'A Bromwich,An Introduction to theTheory of Infinite Series,2nd ed.,Macmillan, London, 1942. K.Knopp,Theorie und Anwendung der UnendlichenReihen,Aufl.4,Springer-Verlag,Berlin,1947.
G.H.Hardy,Divergent Series,Oxford Univ. Press,London, 1949.