分類
排序(Sorting)是計算機程式設計中的一種重要操作,它的功能是將一個數據元素(或記錄)的任意序列,重新排列成一個關鍵字有序的序列。穩定度(穩定性)
一個排序算法是穩定的,就是當有兩個相等記錄的關鍵字R和S,且在原本的列表中R出現在S之前,在排序過的列表中R也將會是在S之前。
當相等的元素是無法分辨的,比如像是整數,穩定度並不是一個問題。然而,假設以下的數對將要以他們的第一個數字來排序。
(4,1)(3,1)(3,7)(5,6)在這個狀況下,有可能產生兩種不同的結果,一個是依照相等的鍵值維持相對的次序,而另外一個則沒有:
(3,1)(3,7)(4,1)(5,6)(維持次序)
(3,7)(3,1)(4,1)(5,6)(次序被改變)
不穩定排序算法可能會在相等的鍵值中改變紀錄的相對次序,但是穩定排序算法從來不會如此。不穩定排序算法可以被特別地實現為穩定。作這件事情的一個方式是人工擴充鍵值的比較,如此在其他方面相同鍵值的兩個對象間之比較,就會被決定使用在原先數據次序中的條目,當作一個同分決賽。然而,要記住這種次序通常牽涉到額外的空間負擔。
在計算機科學所使用的排序算法通常被分類為:
(a)計算的複雜度(最差、平均、和最好性能),依據列表(list)的大小(n)。
一般而言,好的性能是O(nlogn),且壞的性能是O(n^2)。對於一個排序理想的性能是O(n)。
而僅使用一個抽象關鍵比較運算的排序算法總平均上總是至少需要O(nlogn)。
(b)存儲器使用量(空間複雜度)(以及其他電腦資源的使用)。
(c)穩定度:穩定的排序算法會依照相等的關鍵(換言之就是值)維持紀錄的相對次序。
(d)一般的方法:插入、交換、選擇、合併等等。交換排序包含冒泡排序和快速排序。插入排序包含希爾排序,選擇排序包括堆排序等。
C++算法
C++自帶的algorithm庫函式中提供了排序算法。自帶排序算法的一般形式為:
sort(arr+m,arr+n);//將數組arr的下標為m的元素到下標為n-1的元素進行從小到大排序
sort(arr+m,arr+n,comp);//與sort(arr+m,arr+n)相比,這個寫法可以自己定義排序的規則,其中,comp為自定義的函式
對於sort(arr+m,arr+n)我們舉個簡單的例子,這個程式實現從鍵盤讀入10個數,然後從小到大輸出的功能:
| 1 2 3 4 5 6 7 8 9 10 11 12 | #include<algorithm> #include<iostream> usingnamespacestd; main() { inta[10],i; for (i=0;i<10;i++) cin>>a[i]; sort(a,a+10); for (i=0;i<10;i++) cout<<a[i]<< '' ; } |
不過,在調用sort(arr+m,arr+n,comp)之前我們需要自己寫個comp函式。
從大到小排序的comp函式可以這樣寫:
| 1 2 3 4 | intcomp(inta,intb) { returna>b; //在兩元素相同時一定要返回0或者false } |
下面是10個數從大到小排序的代碼:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include<algorithm> #include<iostream> usingnamespacestd; intcomp(inta,intb) { returna>b; //如果a>b則返回1,否則返回0 } main() { inta[10],i; for (i=0;i<10;i++) cin>>a[i]; sort(a,a+10,comp); for (i=0;i<10;i++) cout<<a[i]<< '' ; } |
在更多情況下,我們不僅對一個特徵進行排序,而是多個特徵。例如將學生的成績進行排序,當然用上面的做法是行不通的。這是,我們就想到了結構體這種數據類型。當我們採用sort()函式的默認規則排序結構體時,sort()默認結構體中的第一個成員為第一關鍵字,第二個成員為第二關鍵字,……,第N個元素為第N關鍵字,然後從小到大排序。
例如我們要將學生的成績從大到小排序,當成績相同時,根據姓名字典序小的優先規則進行排序。顯然我們無法採用默認規則進行排序。
這時我們可以定義這樣的comp:
| 1 2 3 4 5 6 7 8 9 10 | intcomp(studenta,studentb) { if (a.score>b.score) return1; if (a.score<b.score) return0; if (a.name<b.name) return1; return0; } |
算法列表
在這個表格中,n是要被排序的紀錄數量以及k是不同鍵值的數量。穩定的
冒泡排序(bubble sort) — O(n2)雞尾酒排序 (Cocktail sort, 雙向的冒泡排序) — O(n2)
插入排序 (insertion sort)— O(n2)
桶排序 (bucket sort)— O(n); 需要 O(k) 額外 記憶體
計數排序 (counting sort) — O(n+k); 需要 O(n+k) 額外 記憶體
歸併排序 (merge sort)— O(n log n); 需要 O(n) 額外記憶體
原地歸併排序 — O(n2)
二叉樹排序 (Binary tree sort) — O(n log n); 需要 O(n) 額外記憶體
鴿巢排序(Pigeonhole sort) — O(n+k); 需要 O(k) 額外記憶體
基數排序(radix sort)— O(n·k); 需要 O(n) 額外記憶體
Gnome sort — O(n2)
Library sort — O(n log n) with high probability, 需要 (1+ε)n 額外記憶體
不穩定
選擇排序 (selection sort)— O(n2)希爾排序 (shell sort)— O(n log n) 如果使用最佳的現在版本
Comb sort — O(n log n)
堆排序 (heapsort)— O(n log n)
Smoothsort — O(n log n)
快速排序 (quicksort)— O(n log n) 期望時間, O(n2) 最壞情況; 對於大的、亂數串列一般相信是最快的已知排序
Introsort — O(n log n)
Patience sorting — O(n log n + k) 最外情況時間, 需要 額外的 O(n + k) 空間, 也需要找到最長的遞增子序列(longest increasing subsequence)
不實用的
Bogo排序 — O(n × n!) 期望時間, 無窮的最壞情況。Stupid sort — O(n3); 遞迴版本需要 O(n2) 額外記憶體
Bead sort — O(n) or O(√n), 但需要特別的硬體
Pancake sorting — O(n), 但需要特別的硬體
排序的算法
排序的算法有很多,對空間的要求及其時間效率也不盡相同。下面列出了一些常見的排序算法。這裡面插入排序和冒泡排序又被稱作簡單排序,他們對空間的要求不高,但是時間效率卻不穩定;而後面三種排序相對於簡單排序對空間的要求稍高一點,但時間效率卻能穩定在很高的水平。基數排序是針對關鍵字在一個較小範圍內的排序算法。插入排序
冒泡排序
選擇排序
快速排序
堆排序
歸併排序
基數排序
希爾排序
插入排序
插入排序是這樣實現的:首先新建一個空列表,用於保存已排序的有序數列(我們稱之為"有序列表")。
從原數列中取出一個數,將其插入"有序列表"中,使其仍舊保持有序狀態。
重複2號步驟,直至原數列為空。
插入排序的平均時間複雜度為平方級的,效率不高,但是容易實現。它藉助了"逐步擴大成果"的思想,使有序列表的長度逐漸增加,直至其長度等於原列表的長度。
冒泡排序
冒泡排序是這樣實現的:首先將所有待排序的數字放入工作列表中。
從列表的第一個數字到倒數第二個數字,逐個檢查:若某一位上的數字大於他的下一位,則將它與它的下一位交換。
重複2號步驟,直至再也不能交換。
冒泡排序的平均時間複雜度與插入排序相同,也是平方級的,但也是非常容易實現的算法。
選擇排序
選擇排序是這樣實現的:設數組記憶體放了n個待排數字,數組下標從1開始,到n結束。
i=1
從數組的第i個元素開始到第n個元素,尋找最小的元素。
將上一步找到的最小元素和第i位元素交換。
如果i=n-1算法結束,否則回到第3步
選擇排序的平均時間複雜度也是O(n²)的。
快速排序
現在開始,我們要接觸高效排序算法了。實踐證明,快速排序是所有排序算法中最高效的一種。它採用了分治的思想:先保證列表的前半部分都小於後半部分,然後分別對前半部分和後半部分排序,這樣整個列表就有序了。這是一種先進的思想,也是它高效的原因。因為在排序算法中,算法的高效與否與列表中數字間的比較次數有直接的關係,而"保證列表的前半部分都小於後半部分"就使得前半部分的任何一個數從此以後都不再跟後半部分的數進行比較了,大大減少了數字間不必要的比較。但查找數據得另當別論了。堆排序
堆排序與前面的算法都不同,它是這樣的:首先新建一個空列表,作用與插入排序中的"有序列表"相同。
找到數列中最大的數字,將其加在"有序列表"的末尾,並將其從原數列中刪除。
重複2號步驟,直至原數列為空。
堆排序的平均時間複雜度為nlogn,效率高(因為有堆這種數據結構以及它奇妙的特徵,使得"找到數列中最大的數字"這樣的操作只需要O(1)的時間複雜度,維護需要logn的時間複雜度),但是實現相對複雜(可以說是這裡7種算法中比較難實現的)。
看起來似乎堆排序與插入排序有些相像,但他們其實是本質不同的算法。至少,他們的時間複雜度差了一個數量級,一個是平方級的,一個是對數級的。
時間複雜度
平均時間複雜度插入排序 O(n2)
冒泡排序 O(n2)
選擇排序 O(n2)
快速排序 O(n log n)
堆排序 O(n log n)
歸併排序 O(n log n)
基數排序 O(n)
希爾排序 O(n1.25)
複雜度
簡單排序算法
由於程式比較簡單,所以沒有加什麼注釋。所有的程式都給出了完整的運行代碼,並在我的VC環境下運行通過。因為沒有涉及MFC和WINDOWS的內容,所以在BORLANDC++的平台上應該也不會有什麼
問題的。在代碼的後面給出了運行過程示意,希望對理解有幫助。
冒泡法
這是最原始,也是眾所周知的最慢的算法了。他的名字的由來因為它的工作看來象是冒泡:| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | #include<iostream> usingnamespacestd; voidBubbleSort( int *pData,intCount) { intiTemp; for (inti=0;i<Count-1;i++) { for (intj=Count-1;j>i;j--) { if (pData[j]<pData[j-1]) { iTemp=pData[j-1]; pData[j-1]=pData[j]; pData[j]=iTemp; } } } } voidmain() { intdata[7]={10,9,8,7,6,5,4}; BubbleSort(data,7); for (inti=0;i<7;i++) { cout<<data[i]<< "" ; } cout<<endl; system ( "PAUSE" ); } |
第一輪:10,9,8,7->10,9,7,8->10,7,9,8->7,10,9,8(交換3次)
第二輪:7,10,9,8->7,10,8,9->7,8,10,9(交換2次)
第一輪:7,8,10,9->7,8,9,10(交換1次)
循環次數:6次
交換次數:6次
其他:
第一輪:8,10,7,9->8,10,7,9->8,7,10,9->7,8,10,9(交換2次)
第二輪:7,8,10,9->7,8,9,10->7,8,10,9(交換1次)
(這是原撰寫人的--7,8,10,9->7,8,10,9->7,8,10,9(交換0次),第二輪應該是這樣的)
第三輪:7,8,9,10->7,8,9,10(交換1次)
循環次數:6次
交換次數:3次
上面我們給出了程式段,現在我們分析它:這裡,影響我們算法性能的主要部分是循環和交換,
顯然,次數越多,性能就越差。從上面的程式我們可以看出循環的次數是固定的,為1+2+...+n-1。
寫成公式就是1/2*(n-1)*n。
現在注意,我們給出O方法的定義:
若存在一常量K和起點n0,使當n>=n0時,有f(n)<=K*g(n),則f(n)=O(g(n))。(呵呵,不要說沒學好數學呀,對於編程數學是非常重要的!!!)
現在我們來看1/2*(n-1)*n,當K=1/2,n0=1,g(n)=n*n時,1/2*(n-1)*n<=1/2*n*n=K*g(n)。所以f(n)
=O(g(n))=O(n*n)。所以我們程式循環的複雜度為O(n*n)。
再看交換。從程式後面所跟的表可以看到,兩種情況的循環相同,交換不同。其實交換本身同數據源的
有序程度有極大的關係,當數據處於倒序的情況時,交換次數同循環一樣(每次循環判斷都會交換),
複雜度為O(n*n)。當數據為正序,將不會有交換。複雜度為O(0)。亂序時處於中間狀態。正是由於這樣的
原因,我們通常都是通過循環次數來對比算法。
交換法
交換法的程式最清晰簡單,每次用當前的元素一一的同其後的元素比較並交換。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | #include<iostream.h> voidExchangeSort( int *pData,intCount) { intiTemp; for (inti=0;i<Count-1;i++) { //共(count-1)輪,每輪得到一個最小值 for (intj=i+1;j<Count;j++) { //每次從剩下的數字中尋找最小值,於當前最小值相比,如果小則交換 if (pData[j]<pData[i]) { iTemp=pData[i]; pData[i]=pData[j]; pData[j]=iTemp; } } } } voidmain() { intdata[]={10,9,8,7,6,5,4}; ExchangeSort(data, sizeof (data)/ sizeof ( int )); for (inti=0;i< sizeof (data)/ sizeof ( int );i++) { cout<<data[i]<< "" ; } cout<<endl; system ( "PAUSE" ); } |
第一輪:9,10,8,7->8,10,9,7->7,10,9,8(交換3次)
第二輪:7,10,9,8->7,9,10,8->7,8,10,9(交換2次)
第一輪:7,8,10,9->7,8,9,10(交換1次)
循環次數:6次
交換次數:6次
其他:
第一輪:8,10,7,9->8,10,7,9->7,10,8,9->7,10,8,9(交換1次)
第二輪:7,10,8,9->7,8,10,9->7,8,10,9(交換1次)
第一輪:7,8,10,9->7,8,9,10(交換1次)
循環次數:6次
交換次數:3次
從運行的表格來看,交換幾乎和冒泡一樣糟。事實確實如此。循環次數和冒泡一樣
也是1/2*(n-1)*n,所以算法的複雜度仍然是O(n*n)。由於我們無法給出所有的情況,所以
只能直接告訴大家他們在交換上面也是一樣的糟糕(在某些情況下稍好,在某些情況下稍差)。
選擇法
現在我們終於可以看到一點希望:選擇法,這種方法提高了一點性能(某些情況下)
這種方法類似我們人為的排序習慣:從數據中選擇最小的同第一個值交換,在從剩下的部分中
選擇最小的與第二個交換,這樣往復下去。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | #include<iostream.h> voidSelectSort( int *pData,intCount) { intiTemp; intiPos; for (inti=0;i<Count-1;i++) { iTemp=pData[i]; iPos=i; for (intj=i+1;j<Count;j++) { if (pData[j]<iTemp) { iTemp=pData[j]; iPos=j; } } pData[iPos]=pData[i]; pData[i]=iTemp; } } voidmain() { intdata[]={10,9,8,7,6,5,4}; SelectSort(data,7); for (inti=0;i<7;i++) cout<<data[i]<< "" ; cout<< "\n" ; } |
第一輪:10,9,8,7->(iTemp=9)10,9,8,7->(iTemp=8)10,9,8,7->(iTemp=7)7,9,8,10(交換1次)
第二輪:7,9,8,10->7,9,8,10(iTemp=8)->(iTemp=8)7,8,9,10(交換1次)
第一輪:7,8,9,10->(iTemp=9)7,8,9,10(交換0次)
循環次數:6次
交換次數:2次
其他:
第一輪:8,10,7,9->(iTemp=8)8,10,7,9->(iTemp=7)8,10,7,9->(iTemp=7)7,10,8,9(交換1次)
第二輪:7,10,8,9->(iTemp=8)7,10,8,9->(iTemp=8)7,8,10,9(交換1次)
第一輪:7,8,10,9->(iTemp=9)7,8,9,10(交換1次)
循環次數:6次
交換次數:3次
遺憾的是算法需要的循環次數依然是1/2*(n-1)*n。所以算法複雜度為O(n*n)。
我們來看他的交換。由於每次外層循環只產生一次交換(只有一個最小值)。所以f(n)<=n
所以我們有f(n)=O(n)。所以,在數據較亂的時候,可以減少一定的交換次數。
插入法
插入法較為複雜,它的基本工作原理是抽出牌,在前面的牌中尋找相應的位置插入,然後繼續下一張| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include<iostream.h> voidInsertSort( int *pData,intCount) { intiTemp; intiPos; for (inti=1;i<Count;i++) { iTemp=pData[i]; //保存要插入的數 iPos=i-1; //被插入的數組數字個數 while ((iPos>=0)&&(iTemp<pData[iPos])) { //從最後一個(最大數字)開始對比,大於它的數字往後移位 pData[iPos+1]=pData[iPos]; iPos--; } pData[iPos+1]=iTemp; //插入數字的位置 } } voidmain(){ intdata[]={10,9,8,7,6,5,4}; InsertSort(data,7); for (inti=0;i<7;i++) cout<<data[i]<< "" ; cout<< "\n" ; } |
第一輪:8,10,7,9->8,10,7,9(交換0次)(循環1次)
第二輪:9,10,8,7->8,9,10,7(交換1次)(循環2次)
第一輪:8,9,10,7->7,8,9,10(交換1次)(循環3次)
循環次數:6次
交換次數:3次
其他:
第一輪:8,10,7,9->8,10,7,9(交換0次)(循環1次)
第二輪:8,10,7,9->7,8,10,9(交換1次)(循環2次)
第一輪:7,8,10,9->7,8,9,10(交換1次)(循環1次)
循環次數:4次
交換次數:2次
上面結尾的行為分析事實上造成了一種假象,讓我們認為這種算法是簡單算法中最好的,其實不是,
因為其循環次數雖然並不固定,我們仍可以使用O方法。從上面的結果可以看出,循環的次數f(n)<=
1/2*n*(n-1)<=1/2*n*n。所以其複雜度仍為O(n*n)(這裡說明一下,其實如果不是為了展示這些簡單
排序的不同,交換次數仍然可以這樣推導)。現在看交換,從外觀上看,交換次數是O(n)(推導類似
選擇法),但我們每次要進行與內層循環相同次數的‘=’操作。正常的一次交換我們需要三次‘=’
而這裡顯然多了一些,所以我們浪費了時間。
最終,我個人認為,在簡單排序算法中,選擇法是最好的。
高級排序算法
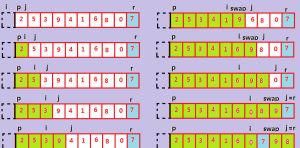
高級排序算法中我們將只介紹這一種,同時也是目前我所知道(我看過的資料中)的最快的。它的工作看起來仍然象一個二叉樹。首先我們選擇一個中間值middle程式中我們使用數組中間值,然後
把比它小的放在左邊,大的放在右邊(具體的實現是從兩邊找,找到一對後交換)。然後對兩邊分別使
用這個過程(最容易的方法——遞歸)。
1.快速排序://這段代碼編譯可以通過,一運行就出錯,內部的細節有些問題,我還沒找到解決方法。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | #include<iostream.h> voidrun( int *pData,intleft,intright) { inti,j; intmiddle,iTemp; i=left; j=right; middle=pData[left]; do { while ((pData[i]<middle)&&(i<right)) //從左掃描大於中值的數 i++; while ((pData[j]>middle)&&(j>left)) //從右掃描大於中值的數 j--; if (i<=j) //找到了一對值 { //交換 iTemp=pData[i]; pData[i]=pData[j]; pData[j]=iTemp; i++; j--; } } while (i<=j); //如果兩邊掃描的下標交錯,就停止(完成一次) //當左邊部分有值(left<j),遞歸左半邊 if (left<j) run(pData,left,j); //當右邊部分有值(right>i),遞歸右半邊 if (right>i) run(pData,i,right); } voidQuickSort( int *pData,intCount) { run(pData,0,Count-1); } voidmain() { intdata[]={10,9,8,7,6,5,4}; QuickSort(data,7); for (inti=0;i<7;i++) cout<<data[i]<< "" ; //原作者此處代碼有誤,輸出因為date[i],date數組名輸出的是地址 cout<< "\n" ; } |
1.數組的大小是2的冪,這樣分下去始終可以被2整除。假設為2的k次方,即k=log2(n)。
2.每次我們選擇的值剛好是中間值,這樣,數組才可以被等分。
第一層遞歸,循環n次,第二層循環2*(n/2)......
所以共有n+2(n/2)+4(n/4)+...+n*(n/n)=n+n+n+...+n=k*n=log2(n)*n
所以算法複雜度為O(log2(n)*n)
批註:n+2(n/2)+4(n/4)+...+n*(n/n)=n+n+n+...+n=k*n=log2(n)*n
為何會=k*n?
其他的情況只會比這種情況差,最差的情況是每次選擇到的middle都是最小值或最大值,那么他將變
成交換法(由於使用了遞歸,情況更糟)。但是你認為這種情況發生的幾率有多大??呵呵,你完全
不必擔心這個問題。實踐證明,大多數的情況,快速排序總是最好的。
如果你擔心這個問題,你可以使用堆排序,這是一種不穩定的O(log2(n)*n)算法,但是通常情況下速度要慢
於快速排序(因為要重組堆)。
其他排序
雙向冒泡
通常的冒泡是單向的,而這裡是雙向的,也就是說還要進行反向的工作。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include<iostream.h> inlinevoidexchange( int *a, int *b) { inttemp; temp=*a; *a=*b; *b=temp; } voidbubblesort( int *array,intnum) { inti,j,k,flag=0; for (i=0;i<num;i++){ printf ( "%d" ,array[i]); } printf ( "\n" ); for (i=0;i<num;i++){ //所有數的個數為num個 flag=0; for (j=i;j<num-i-1;j++){ //每循環一次最底端的數的順序都會排好,所以初始時j=i; if (array[j]>array[j+1]){ exchange(&array[j],&array[j+1]); flag=1; } } for (k=num-1-i-1;k>i;k--){ //每循環一次最頂端的數據的順序也會排好,所以初始時k=num-i-2 if (array[k]<array[k-1]){ exchange(&array[k],&array[k-1]); flag=1; } } if (flag==0){ //如果flag未發生改變則說明未發生數據交換,則排序完成 return ; } } } voidmain() { intdata[]={10,9,8,7,6,5,4,3,2,1,-10,-1}; bubblesort(data,12); for (inti=0;i<12;i++) cout<<data<< "" ; cout<< "\n" ; } |
通用排序
這個程式我想就沒有分析的必要了,大家看一下就可以了。不明白可以在論壇上問。MyData.h檔案
///////////////////////////////////////////////////////
classCMyData
{
public:
CMyData(intIndex,char*strData);
CMyData();
virtual~CMyData();
intm_iIndex;
intGetDataSize(){returnm_iDataSize;};
constchar*GetData(){returnm_strDatamember;};
//這裡重載了操作符:
CMyData&operator=(CMyData&SrcData);
booloperator<(CMyData&data);
booloperator>(CMyData&data);
private:
char*m_strDatamember;
intm_iDataSize;
};
////////////////////////////////////////////////////////
MyData.cpp檔案
////////////////////////////////////////////////////////
CMyData::CMyData():
m_iIndex(0),
m_iDataSize(0),
m_strDatamember(NULL)
{
}
CMyData::~CMyData()
{
if(m_strDatamember!=NULL)
delete[]m_strDatamember;
m_strDatamember=NULL;
}
CMyData::CMyData(intIndex,char*strData):
m_iIndex(Index),
m_iDataSize(0),
m_strDatamember(NULL)
{
m_iDataSize=strlen(strData);
m_strDatamember=newchar[m_iDataSize+1];
strcpy(m_strDatamember,strData);
}
CMyData&CMyData::operator=(CMyData&SrcData)
{
m_iIndex=SrcData.m_iIndex;
m_iDataSize=SrcData.GetDataSize();
m_strDatamember=newchar[m_iDataSize+1];
strcpy(m_strDatamember,SrcData.GetData());
return*this;
}
boolCMyData::operator<(CMyData&data)
{
returnm_iIndex<data.m_iIndex;
}
boolCMyData::operator>(CMyData&data)
{
returnm_iIndex>data.m_iIndex;
}
///////////////////////////////////////////////////////////
//////////////////////////////////////////////////////////
//主程式部分
#include<iostream.h>
#include"MyData.h"
template<classT>
voidrun(T*pData,intleft,intright)
{
inti,j;
Tmiddle,iTemp;
i=left;
j=right;
//下面的比較都調用我們重載的操作符函式
middle=pData[(left+right)/2];//求中間值
do{
while((pData<middle)&&(i<right))//從左掃描大於中值的數
i++;
while((pData[j]>middle)&&(j>left))//從右掃描大於中值的數
j--;
if(i<=j)//找到了一對值
{
//交換
iTemp=pData;
pData=pData[j];
pData[j]=iTemp;
i++;
j--;
}
}while(i<=j);//如果兩邊掃描的下標交錯,就停止(完成一次)
//當左邊部分有值(left<j),遞歸左半邊
if(left<j)
run(pData,left,j);
//當右邊部分有值(right>i),遞歸右半邊
if(right>i)
run(pData,i,right);
}
template<classT>
voidQuickSort(T*pData,intCount)
{
run(pData,0,Count-1);
}
voidmain()
{
CMyDatadata[]={
CMyData(8,"xulion"),
CMyData(7,"sanzoo"),
CMyData(6,"wangjun"),
CMyData(5,"VCKBASE"),
CMyData(4,"jacky2000"),
CMyData(3,"cwally"),
CMyData(2,"VCUSER"),
CMyData(1,"isdong")
};
QuickSort(data,8);
for(inti=0;i<8;i++)
cout<<data.m_iIndex<<""<<data.GetData()<<"\n";
cout<<"\n";
經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科,就像一個人的思維能力一樣,其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展,新的算法也隨著新的套用漸漸出現,但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典,本任務就是要介紹這些經典算法。 |