基本解法
第一步
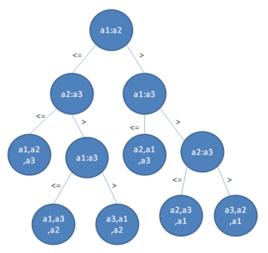
以LSD為例,假設原來有一串數值如下所示:
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
首先根據個位數的數值,在走訪數值時將它們分配至編號0到9的桶子中:
0
1 81
2 22
3 73 93 43
4 14
5 55 65
6
7
8 28
9 39
第二步
接下來將這些桶子中的數值重新串接起來,成為以下的數列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接著再進行一次分配,這次是根據十位數來分配:
0
1 14
2 22 28
3 39
4 43
5 55
6 65
7 73
8 81
9 93
第三步
接下來將這些桶子中的數值重新串接起來,成為以下的數列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
這時候整個數列已經排序完畢;如果排序的對象有三位數以上,則持續進行以上的動作直至最高位數為止。
LSD的基數排序適用於位數小的數列,如果位數多的話,使用MSD的效率會比較好。MSD的方式與LSD相反,是由高位數為基底開始進行分配,但在分配之後並不馬上合併回一個數組中,而是在每個“桶子”中建立“子桶”,將每個桶子中的數值按照下一數位的值分配到“子桶”中。在進行完最低位數的分配後再合併回單一的數組中。
效率分析
時間效率 :設待排序列為n個記錄,d個關鍵碼,關鍵碼的取值範圍為radix,則進行鏈式基數排序的時間複雜度為O(d(n+radix)),其中,一趟分配時間複雜度為O(n),一趟收集時間複雜度為O(radix),共進行d趟分配和收集。 空間效率:需要2*radix個指向佇列的輔助空間,以及用於靜態鍊表的n個指針。
實現方法
最高位優先(Most Significant Digit first)法,簡稱MSD法:先按k1排序分組,同一組中記錄,關鍵碼k1相等,再對各組按k2排序分成子組,之後,對後面的關鍵碼繼續這樣的排序分組,直到按最次位關鍵碼kd對各子組排序後。再將各組連線起來,便得到一個有序序列。
最低位優先(Least Significant Digit first)法,簡稱LSD法:先從kd開始排序,再對kd-1進行排序,依次重複,直到對k1排序後便得到一個有序序列。
實現原理
基數排序的發明可以追溯到1887年赫爾曼·何樂禮在打孔卡片制表機(Tabulation Machine)上的貢獻。它是這樣實現的:將所有待比較數值(正整數)統一為同樣的數位長度,數位較短的數前面補零。然後,從最低位開始,依次進行一次排序。這樣從最低位排序一直到最高位排序完成以後, 數列就變成一個有序序列。
基數排序的方式可以採用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由鍵值的最右邊開始,而MSD則相反,由鍵值的最左邊開始。
實現
C語言
Java語言
pascal
c++
C# 實現基數排序
python 實現
AAuto
第一步
io.open();//打開控制台
/*
*-------------------------------------------------------
* 基數排序
**------------------------------------------------------
*/
/*
第二步
基數排序從低位到高位進行,使得最後一次計數排序完成後,數組有序。
其原理在於對於待排序的數據,整體權重未知的情況下,
先按權重小的因子排序,然後按權重大的因子排序。
例如比較時間,先按日排序,再按月排序,最後按年排序,僅需排序三次。
但是如果先排序高位就沒這么簡單了。
基數排序源於老式穿孔機,排序器每次只能看到一個列,
很多教科書上的基數排序都是對數值排序,數值的大小是已知的,與老式穿孔機不同。
將數值按位拆分再排序,是無聊並自找麻煩的事。
算法的目的是找到最佳解決問題的方案,而不是把簡單的事搞的更複雜。
基數排序更適合用於對時間、字元串等這些整體權值未知的數據進行排序。
這時候基數排序的思想才能體現出來,例如字元串,如果從高位(第一位)往後排就很麻煩。
而反過來,先對影響力較小,排序排重因子較小的低位(最後一位)進行排序就非常簡單了。
這時候基數排序的思想就能體現出來。
又或者所有的數值都是以字元串形式存儲,就象穿孔機一樣,每次只能對一列進行排序。
這時候基數排序也適用,例如:對{"193";"229";"233";"215"}進行排序
下面我們使用基數排序對字元串進行排序。
對每個位循環調用計數排序。
*/
第三步
//計數排序算法
radix_sort = function( array ,maxlen){
//AAuto在字元串索引越界時,會返回0,這使基數排序的實現更加簡單。
//我們首先找出最大的排序長度,然後對於不足此長度的字元串,尾部都假定以0補齊。
//對於超出此長度的位在比較時忽略
if(!maxlen){
maxlen =0;
for(i=1;#array;1){
maxlen = math.max(maxlen,#array[i] )
}
}
//else{
//最大排序長度也可以從參數中傳過來,這樣就不用遍歷所有字元串了
//}
第四步
//從字元串的最後一位開始,到第一位
for(pos=maxlen;1;-1){
//按當前位的位元組碼計數排序
var array_sorted ={};
var count = {};
for(i=0;256 ){
count[i] = 0;
}
var bytecode;
for(i=1;#array;1){
//如果pos大於字元串長度,AAuto會返回0,這使基數排序的實現更容易
bytecode = array[i][pos] ;
count[ bytecode ] ++; //count[n] 包含等於n的個數
}
第五步
//統計位置
for(i=1;256;1){
count[i] += count[i-1]; //count[i] 包含小於等於i的個數
}
var n;
for(i=#array;1;-1){
n = array[i][pos]
array_sorted[ count[n] ] = array[i];
count[n]--;//防止相同的元素n再次出現,將計數減一
}
array = array_sorted;
}
return array
}
io.print("----------------")
io.print("基數排序( 線性時間排序 )")
io.print("----------------")
array ={"AAuto is quicker and better,just try it!";"AAuto Quicker";"193";"229";"233";"215";"Hello Word";"abc";"abcd";"xd";"adcd";"eddd";"ah";"ai";"aj";"ajkk"};
第六步
//排序
array = radix_sort(array )
第七步
//輸出結果
for(i=1;#array;1){
io.print( array[i] )
}
execute("pause") //按任意鍵繼續
io.close();//關閉控制台