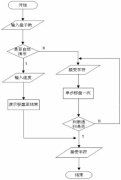
遞歸程式
在支持自調用的程式語言中,遞歸可以通過簡單的函式調用來完成,如計算階乘的程式在數學上可以定義為:
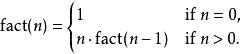 遞歸算法
遞歸算法這一程式在Scheme語言中可以寫作:
不動點組合子
即使一個程式語言不支持自調用,如果在這語言中函式是第一類對象(即可以在運行期創建並作為變數處理),遞歸可以通過不動點組合子(英語:Fixed-point combinator)來產生。以下Scheme程式沒有用到自調用,但是利用了一個叫做Z 運算元(英語:Z combinator)的不動點組合子,因此同樣能達到遞歸的目的。
這一程式思路是,既然在這裡函式不能調用其自身,我們可以用 Z 組合子套用(application)這個函式後得到的函式再套用需計算的參數。
尾部遞歸
尾部遞歸是指遞歸函式在調用自身後直接傳回其值,而不對其再加運算。尾部遞歸與循環是等價的,而且在一些語言(如Scheme中)可以被最佳化為循環指令。 因此,在這些語言中尾部遞歸不會占用調用堆疊空間。以下Scheme程式同樣計算一個數字的階乘,但是使用尾部遞歸:
能夠解決的問題
數據的定義是按遞歸定義的。如Fibonacci函式。
問題解法按遞歸算法實現。如Hanoi問題。
數據的結構形式是按遞歸定義的。如二叉樹、廣義表等。
1.數據的定義是按遞歸定義的。如Fibonacci函式。
2.問題解法按遞歸算法實現。如Hanoi問題。
3.數據的結構形式是按遞歸定義的。如二叉樹、廣義表等。
遞歸數據
數據類型可以通過遞歸來進行定義,比如一個簡單的遞歸定義為自然數的定義:“一個自然數或等於0,或等於另一個自然數加上1”。Haskell中可以定義鍊表為:
這一定義相當於宣告“一個鍊表或是空串列,或是一個鍊表之前加上一個字元串”。可以看出所有鍊表都可以通過這一遞歸定義來達到。
經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科,就像一個人的思維能力一樣,其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展,新的算法也隨著新的套用漸漸出現,但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典,本任務就是要介紹這些經典算法。 |