簡介
衡量一個算法的優劣有許多因素，效率就是其中之一。而效率指的就是算法的執行時間。提高效率是軟體開發必須注重的問題。對同一個問題往往有多個算法可以解決，在同等條件下,執行時間短的算法其效率是最高的。從霍夫曼樹的定義以及霍夫曼算法出發，介紹如何構造霍夫曼樹以及利用霍夫曼算法最佳化程式設計的原理，重點討論在判定類問題中利用霍夫曼樹可以建立最佳判定算法，提高程式的執行速度。
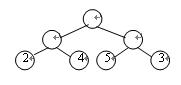
圖.最優二叉樹
引入
在實際套用中，常常要考慮一個問題：如何設計一棵二叉樹，使得執行路徑最短，即算法的效率最高。
例1.快遞包裹的郵資問題
假設郵政局的包裹自動測試系統能夠測出包裹的重量，如何設計一棵二叉樹將包裹根據重量及運距進行分類從而確定郵資。
國內快遞包裹資費 單位：元
（2004年1月1日起執行）
| 運距（公里） | 首重1000克 | 5000克以內續重每500克 | 5001克以上續重每500克 |
| <=500 | 5.00 | 2.00 | 1.00 |
| <=1000 >500 | 6.00 | 2.50 | 1.30 |
| <=1500 >1000 | 7.00 | 3.00 | 1.60 |
| <=2000 >1500 | 8.00 | 3.50 | 1.90 |
| <=2500 >2000 | 9.00 | 4.00 | 2.20 |
| <=3000 >2500 | 10.00 | 4.50 | 2.50 |
| <=4000 >3000 | 12.00 | 5.50 | 3.10 |
| <=5000 >4000 | 14.00 | 6.50 | 3.70 |
| <=6000 >5000 | 16.00 | 7.50 | 4.30 |
| >6000 | 20.00 | 9.00 | 6.00 |
表1 國家郵政局制定的快遞包裹參考標準
根據表1可以制定出許多種二叉樹，但不同的二叉樹判定的次數可能不一樣，執行的效率也不同。
例2 鐵球分類
現有一批球磨機上的鐵球，需要將它分成四類：直徑不大於20的屬於第一類;直徑大於20而不大於50的屬於第二類；直徑大於50而不大於100的屬於第三類；其餘的屬於第四類；假定這批球中屬於第一、二、三、四類鐵球的個數之比例是1:2:3:4。
我們可以把這個判斷過程表示為 圖1中的兩種方法：
| 最優二叉樹算法 |
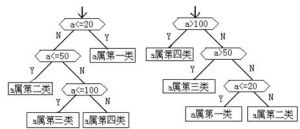（圖）最優二叉樹算法圖1 兩種判斷二叉樹示意圖
那么究竟將這個判斷過程表示成哪一個判斷框，才能使其執行時間最短呢？讓我們對上述判斷框做一具體的分析。
假設有1000個鐵球，則各類鐵球的個數分別為：100、200、300、400；
對於圖7.1中的左圖和右圖比較的次數分別如表2所示：
左圖右圖
| 序號 | 比較式 | 比較次數 |
| 1 | a<20 | 1000 |
| 2 | a<50 | 900 |
| 3 | a<=100 | 700 |
| 合計 | 2600 |
| 序號 | 比較式 | 比較次數 |
| 1 | a>100 | 1000 |
| 2 | a>50 | 600 |
| 3 | a<=20 | 300 |
| 合計 | 1900 |
表2 兩種判斷二叉樹比較次數
過上述分析可知，圖1中右圖所示的判斷框的比較次數遠遠小於左圖所示的判斷框的比較次數。為了找出比較次數最少的判斷框，將涉及到樹的路徑長度問題。
基本概念
最優二叉樹，也稱哈夫曼（Haffman）樹，是指對於一組帶有確定權值的葉結點，構造的具有最小帶權路徑長度的二叉樹。
那么什麼是二叉樹的帶權路徑長度呢？
在前面我們介紹過路徑和結點的路徑長度的概念，而二叉樹的路徑長度則是指由根結點到所有葉結點的路徑長度之和。如果二叉樹中的葉結點都具有一定的權值，則可將這一概念加以推廣。設二叉樹具有n個帶權值的葉結點，那么從根結點到各個葉結點的路徑長度與相應結點權值的乘積之和叫做二叉樹的帶權路徑長度，記為：
wpl＝ Wk•Lk
其中Wk為第k個葉結點的權值，Lk 為第k個葉結點的路徑長度。如圖7.2所示的二叉樹，它的帶權路徑長度值WPL＝2×2＋4×2＋5×2＋3×2＝28。
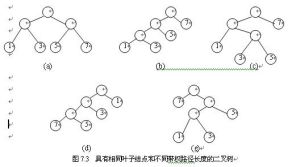
在給定一組具有確定權值的葉結點，可以構造出不同的帶權二叉樹。例如，給出4個葉結點，設其權值分別為1，3，5，7，我們可以構造出形狀不同的多個二叉樹。這些形狀不同的二叉樹的帶權路徑長度將各不相同。圖7.3給出了其中5個不同形狀的二叉樹。
這五棵樹的帶權路徑長度分別為：
（a）WPL＝1×2＋3×2＋5×2＋7×2＝32
（b）WPL＝1×3＋3×3＋5×2＋7×1＝29
（c）WPL＝1×2＋3×3＋5×3＋7×1＝33
（d）WPL＝7×3＋5×3＋3×2＋1×1＝43
（e）WPL＝7×1＋5×2＋3×3＋1×3＝29
最優二叉樹算法圖2 一個帶權二叉樹
最優二叉樹算法由此可見，由相同權值的一組葉子結點所構成的二叉樹有不同的形態和不同的帶權路徑長度，那么如何找到帶權路徑長度最小的二叉樹（即哈夫曼樹）呢？根據哈夫曼樹的定義，一棵二叉樹要使其WPL值最小，必須使權值越大的葉結點越靠近根結點，而權值越小的葉結點越遠離根結點。
哈夫曼（Haffman）依據這一特點於1952年提出了一種方法，這種方法的基本思想是：
（1）由給定的n個權值{W1，W2，…，Wn}構造n棵只有一個葉結點的二叉樹，從而得到一個二叉樹的集合F＝{T1，T2，…，Tn}；
（2）在F中選取根結點的權值最小和次小的兩棵二叉樹作為左、右子樹構造一棵新的二叉樹，這棵新的二叉樹根結點的權值為其左、右子樹根結點權值之和；
（3）在集合F中刪除作為左、右子樹的兩棵二叉樹，並將新建立的二叉樹加入到集合F中；
（4）重複（2）（3）兩步，當F中只剩下一棵二叉樹時，這棵二叉樹便是所要建立的哈夫曼樹。
構造算法
從上述算法中可以看出，F實際上是森林，該算法的思想是不斷地進行森林F中的二叉樹的“合併”，最終得到哈夫曼樹。
在構造哈夫曼樹時，可以設定一個結構數組HuffNode保存哈夫曼樹中各結點的信息，根據二叉樹的性質可知，具有n個葉子結點的哈夫曼樹共有2n－1個結點，所以數組HuffNode的大小設定為2n－1，數組元素的結構形式如下：
| weight | lchild | rchild | parent |
其中，weight域保存結點的權值，lchild和rchild域分別保存該結點的左、右孩子結點在數組HuffNode中的序號，從而建立起結點之間的關係。為了判定一個結點是否已加入到要建立的哈夫曼樹中，可通過parent域的值來確定。初始時parent的值為－1，當結點加入到樹中時，該結點parent的值為其雙親結點在數組HuffNode中的序號，就不會是－1了。
構造哈夫曼樹時，首先將由n個字元形成的n個葉結點存放到數組HuffNode的前n個分量中，然後根據前面介紹的哈夫曼方法的基本思想，不斷將兩個小子樹合併為一個較大的子樹，每次構成的新子樹的根結點順序放到HuffNode數組中的前n個分量的後面。
下面給出哈夫曼樹的構造算法。
const maxvalue= 10000; {定義最大權值}
maxleat=30; {定義哈夫曼樹中葉子結點個數}
maxnode=maxleaf*2-1;
type HnodeType=record
weight: integer;
parent: integer;
lchild: integer;
rchild: integer;
end;
HuffArr:array[0..maxnode] of HnodeType;
var ……
procedure CreatHaffmanTree(var HuffNode: HuffArr); {哈夫曼樹的構造算法}
var i,j,m1,m2,x1,x2,n: integer;
begin
readln(n); {輸入葉子結點個數}
for i:=0 to 2*n-1 do {數組HuffNode[ ]初始化}
begin
HuffNode[i].weight=0;
HuffNode[i].parent=-1;
HuffNode[i].lchild=-1;
HuffNode[i].rchild=-1;
end;
for i:=0 to n-1 do read(HuffNode[i].weight); {輸入n個葉子結點的權值}
for i:=0 to n-1 do {構造哈夫曼樹}
begin
m1:=MAXVALUE; m2:=MAXVALUE;
x1:=0; x2:=0;
for j:=0 to n i-1 do
if (HuffNode[j].weight
begin m2:=m1; x2:=x1;
m1:=HuffNode[j].weight; x1:=j;
end
else if (HuffNode[j].weight
begin m2:=HuffNode[j].weight; x2:=j; end;
{將找出的兩棵子樹合併為一棵子樹}
HuffNode[x1].parent:=n i; HuffNode[x2].parent:=n i;
HuffNode[n i].weight:= HuffNode[x1].weight HuffNode[x2].weight;
HuffNode[n i].lchild:=x1; HuffNode[n i].rchild:=x2;
end;
end;
在編碼問題中的套用
在數據通訊中，經常需要將傳送的文字轉換成由二進制字元0，1組成的二進制串，我們稱之為編碼。例如，假設要傳送的電文為ABACCDA，電文中只含有A，B，C，D四種字元，若這四種字符采用表7.3 (a)所示的編碼，則電文的代碼為000010000100100111 000，長度為21。在傳送電文時，我們總是希望傳送時間儘可能短，這就要求電文代碼儘可能短，顯然，這種編碼方案產生的電文代碼不夠短。表7.3 (b)所示為另一種編碼方案，用此編碼對上述電文進行編碼所建立的代碼為00010010101100，長度為14。在這種編碼方案中，四種字元的編碼均為兩位，是一種等長編碼。如果在編碼時考慮字元出現的頻率，讓出現頻率高的字元採用儘可能短的編碼，出現頻率低的字元採用稍長的編碼，構造一種不等長編碼，則電文的代碼就可能更短。如當字元A，B，C，D採用表7.3 (c)所示的編碼時，上述電文的代碼為0110010101110，長度僅為13。
表a表b表c表d
| 字元 | 編碼 |
| A | 000 |
| B | 010 |
| C | 100 |
| D | 111 |
| 字元 | 編碼 |
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
| 字元 | 編碼 |
| A | 0 |
| B | 110 |
| C | 10 |
| D | 111 |
| 字元 | 編碼 |
| A | 01 |
| B | 010 |
| C | 001 |
| D | 10 |
表3 字元的四種不同的編碼方案
哈夫曼樹可用於構造使電文的編碼總長最短的編碼方案。具體做法如下：設需要編碼的字元集合為{d1，d2，…，dn}，它們在電文中出現的次數或頻率集合為{w1，w2，…，wn}，以d1，d2，…，dn作為葉結點，w1，w2，…，wn作為它們的權值，構造一棵哈夫曼樹，規定哈夫曼樹中的左分支代表0，右分支代表1，則從根結點到每個葉結點所經過的路徑分支組成的0和1的序列便為該結點對應字元的編碼，我們稱之為哈夫曼編碼。
在哈夫曼編碼樹中，樹的帶權路徑長度的含義是各個字元的碼長與其出現次數的乘積之和，也就是電文的代碼總長，所以採用哈夫曼樹構造的編碼是一種能使電文代碼總長最短的不等長編碼。
在建立不等長編碼時，必須使任何一個字元的編碼都不是另一個字元編碼的前綴，這樣才能保證解碼的唯一性。例如表7.3 (d)的編碼方案，字元A的編碼01是字元B的編碼010的前綴部分，這樣對於代碼串0101001，既是AAC的代碼，也是ABD和BDA的代碼，因此，這樣的編碼不能保證解碼的唯一性，我們稱之為具有二義性的解碼。
然而，採用哈夫曼樹進行編碼，則不會產生上述二義性問題。因為，在哈夫曼樹中，每個字元結點都是葉結點，它們不可能在根結點到其它字元結點的路徑上，所以一個字元的哈夫曼編碼不可能是另一個字元的哈夫曼編碼的前綴，從而保證了解碼的非二義性。
下面討論實現哈夫曼編碼的算法。實現哈夫曼編碼的算法可分為兩大部分：
（1）構造哈夫曼樹；
（2）在哈夫曼樹上求葉結點的編碼。
求哈夫曼編碼，實質上就是在已建立的哈夫曼樹中，從葉結點開始，沿結點的雙親鏈域回退到根結點，每回退一步，就走過了哈夫曼樹的一個分支，從而得到一位哈夫曼碼值，由於一個字元的哈夫曼編碼是從根結點到相應葉結點所經過的路徑上各分支所組成的0，1序列，因此先得到的分支代碼為所求編碼的低位碼，後得到的分支代碼為所求編碼的高位碼。我們可以設定一結構數組HuffCode用來存放各字元的哈夫曼編碼信息，數組元素的結構如下：
| bit | start |
其中，分量bit為一維數組，用來保存字元的哈夫曼編碼，start表示該編碼在數組bit中的開始位置。所以，對於第i個字元，它的哈夫曼編碼存放在HuffCode[i].bit中的從HuffCode[i].start到n的分量上。
求哈夫曼編碼程式段
const Maxleaf=128; {定義最多葉結點數}
MaxNode=255; {定義最大結點數}
MaxBit=10; {定義哈夫曼編碼的最大長度}
type HCodeType =record
bit: array[0..MaxBit] of integer;
start: integer;
end;
……
procedure HaffmanCode ; {生成哈夫曼編碼}
var HuffNode: array[0..MaxNode] of HCodeType;
HuffCode: array[0..MaxLeaf] of HcodeType;
cd : HcodeType ;
i,j, c,p: integer ;
begin
HuffmanTree (HuffNode ); {建立哈夫曼樹}
for i:=0 to n-1 do {求每個葉子結點的哈夫曼編碼}
begin
cd.start:=n-1; c:=i;
p:=HuffNode[c].parent;
while p<>0 do {由葉結點向上直到樹根}
if HuffNode[p].lchild=c then cd.bit[cd.start]:=0
else cd.bit[cd.start]:=1;
dec (cd.start); c:=p;
p:=HuffNode[c].parent;
end;
for j:=cd.start 1 to n-1 do {保存求出的每個葉結點的哈夫曼編碼和編碼的起始位}
begin
HuffCode[i].bit[j]:=cd.bit[j];
HuffCode[i].start=cd.start;
end;
for i:=0 to n-1 do {輸出每個葉子結點的哈夫曼編碼}
begin
for j:=HuffCode[i].start 1 to n-1 do write(HuffCode[i].bit[j]:10);
writeln;
end;
end;
檔案的編碼和解碼
通過從上一節的學習，我們知道了如何利用哈夫曼樹來構造字元編碼。有了字元集的哈夫曼編碼表之後，對數據檔案的編碼過程是：依次讀人檔案中的字元c，在哈夫曼編碼表H中找到此字元，若H[i].ch=c，則將字元c轉換為H[i].bits中存放的編碼串。
對壓縮後的數據檔案進行解碼則必須藉助於哈夫曼樹T，其過程是：依次讀人檔案的二進制碼，從哈夫曼樹的根結點(即T[m-1])出發，若當前讀人0，則走向左孩子，否則走向右孩子。一旦到達某一葉子T[i]時便譯出相應的字元H[i].ch。然後重新從根出發繼續解碼，直至檔案結束。
在判定問題中的套用
在本章的引入部分，兩個例子都是判定問題，這兩個判定問題都可以通過構造哈夫曼樹來最佳化判定，以達到總的判定次數最少。
再如，要編制一個將百分制轉換為五級分制的程式。顯然，此程式很簡單，只要利用條件語句便可完成。
程式段
if a<60 then b:=’bad’
else if a<70 then b:=’pass’
else if a<80 then b:=’general’
else if a<90 then b:=’good’
else b:=’excellent’;
如果上述程式需反覆使用，而且每次的輸入量很大，則應考慮上述程式的質量問題，即其操作所需要的時間。因為在實際中，學生的成績在五個等級上的分布是不均勻的，假設其分布規律如表4所示：
| 分數 | 0-59 | 60－69 | 70－79 | 80－89 | 90－100 |
| 比例數 | 0.05 | 0.15 | 0.40 | 0.30 | 0.10 |
表4 分數段的分布頻率
則80％以上的數據需進行三次或三次以上的比較才能得出結果。假定以5，15，40，30和10為權構造一棵有五個葉子結點的哈夫曼樹，它可使大部分的數據經過較少的比較次數得出結果。但由於每個判定框都有兩次比較，將這兩次比較分開，得到新的判定樹，按此判定樹可寫出相應的程式。請您自己畫出此判定樹。
假設有10000個輸入數據，若上程式段的判定過程進行操作，則總共需進行31500次比較；而若新判定樹的判定過程進行操作，則總共僅需進行22000次比較。
經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科，就像一個人的思維能力一樣，其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展，新的算法也隨著新的套用漸漸出現，但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典，本任務就是要介紹這些經典算法。 |
