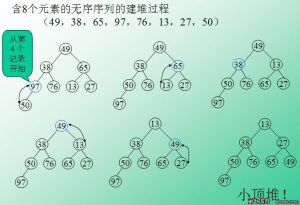
計算起源
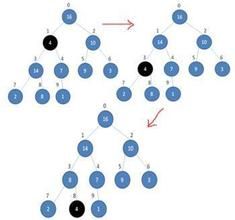 堆排序
堆排序堆排序定義
 堆排序
堆排序(1) ki≤K2i且ki≤K2i+1 或(2)Ki≥K2i且ki≥K2i+1(1≤i≤ )
若將此序列所存儲的向量R【1..n】看做是一棵完全二叉樹的存儲結構,則堆實質上是滿足如下性質的完全二叉樹:樹中任一非葉結點的關鍵字均不大於(或不小於)其左右孩子(若存在)結點的關鍵字。
【例】關鍵字序列(10,15,56,25,30,70)和(70,56,30,25,15,10)分別滿足堆性質(1)和(2),故它們均是堆,其對應的完全二叉樹分別如小根堆示例和大根堆示例所示。
堆的概念
根結點(亦稱為堆頂)的關鍵字是堆里所有結點關鍵字中最小者的堆稱為小根堆。根結點(亦稱為堆頂)的關鍵字是堆里所有結點關鍵字中最大者,稱為大根堆。
注意:
①堆中任一子樹亦是堆。
②以上討論的堆實際上是二叉堆(Binary Heap),類似地可定義k叉堆。
排序特點
堆排序(HeapSort)是一樹形選擇排序。堆排序的特點是:在排序過程中,將R【l..n】看成是一棵完全二叉樹的順序存儲結構,利用完全二叉樹中雙親結點和孩子結點之間的內在關係【參見二叉樹的順序存儲結構】,在當前無序區中選擇關鍵字最大(或最小)的記錄。
算法分析
堆排序的時間,主要由建立初始堆和反覆重建堆這兩部分的時間開銷構成,它們均是通過調用Heapify實現的。平均性能
O(N*logN)。
其他性能
由於建初始堆所需的比較次數較多,所以堆排序不適宜於記錄數較少的檔案。
堆排序是就地排序,輔助空間為O(1).
它是不穩定的排序方法。(排序的穩定性是指如果在排序的序列中,存在前後相同的兩個元素的話,排序前和排序後他們的相對位置不發生變化)
排序區別
直接選擇排序中,為了從R【1..n】中選出關鍵字最小的記錄,必須進行n-1次比較,然後在R【2..n】中選出關鍵字最小的記錄,又需要做n-2次比較。事實上,後面的n-2次比較中,有許多比較可能在前面的n-1次比較中已經做過,但由於前一趟排序時未保留這些比較結果,所以後一趟排序時又重複執行了這些比較操作。堆排序可通過樹形結構保存部分比較結果,可減少比較次數。
堆排序
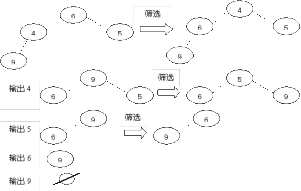 堆排序過程
堆排序過程(1)用大根堆排序的基本思想
① 先將初始檔案R【1..n】建成一個大根堆,此堆為初始的無序區
② 再將關鍵字最大的記錄R【1】(即堆頂)和無序區的最後一個記錄R【n】交換,由此得到新的無序區R【1..n-1】和有序區R【n】,且滿足R【1..n-1】.keys≤R【n】.key
③ 由於交換後新的根R【1】可能違反堆性質,故應將當前無序區R【1..n-1】調整為堆。然後再次將R【1..n-1】中關鍵字最大的記錄R【1】和該區間的最後一個記錄R【n-1】交換,由此得到新的無序區R【1..n-2】和有序區R【n-1..n】,且仍滿足關係R【1..n-2】.keys≤R【n-1..n】.keys,同樣要將R【1..n-2】調整為堆。
直到無序區只有一個元素為止。
(2)大根堆排序算法的基本操作:
① 初始化操作:將R【1..n】構造為初始堆;
② 每一趟排序的基本操作:將當前無序區的堆頂記錄R【1】和該區間的最後一個記錄交換,然後將新的無序區調整為堆(亦稱重建堆)。
注意:
①只需做n-1趟排序,選出較大的n-1個關鍵字即可以使得檔案遞增有序。
②用小根堆排序與利用大根堆類似,只不過其排序結果是遞減有序的。堆排序和直接選擇排序相反:在任何時刻,堆排序中無序區總是在有序區之前,且有序區是在原向量的尾部由後往前逐步擴大至整個向量為止。
(3)堆排序的算法:
void HeapSort(SeqIAst R)
{ //對R【1..n】進行堆排序,不妨用R【0】做暫存單元
int i;
BuildHeap(R); //將R【1-n】建成初始堆
for(i=n;i>1;i--){ //對當前無序區R【1..i】進行堆排序,共做n-1趟。
R【0】=R【1】;R【1】=R;R=R【0】; //將堆頂和堆中最後一個記錄交換
Heapify(R,1,i-1); //將R【1..i-1】重新調整為堆,僅有R【1】可能違反堆性質
} //endfor
} //HeapSort
(4) BuildHeap和Heapify函式的實現
因為構造初始堆必須使用到調整堆的操作,先討論Heapify的實現。
① Heapify函式思想方法
每趟排序開始前R【l..i】是以R【1】為根的堆,在R【1】與R交換後,新的無序區R【1..i-1】中只有R【1】的值發生了變化,故除R【1】可能違反堆性質外,其餘任何結點為根的子樹均是堆。因此,當被調整區間是R【low..high】時,只須調整以R【low】為根的樹即可。
"篩選法"調整堆
R【low】的左、右子樹(若存在)均已是堆,這兩棵子樹的根R【2low】和R【2low+1】分別是各自子樹中關鍵字最大的結點。若R【low】.key不小於這兩個孩子結點的關鍵字,則R【low】未違反堆性質,以R【low】為根的樹已是堆,無須調整;否則必須將R【low】和它的兩個孩子結點中關鍵字較大者進行交換,即R【low】與R【large】(R【large】.key=max(R【2low】.key,R【2low+1】.key))交換。交換後又可能使結點R【large】違反堆性質,同樣由於該結點的兩棵子樹(若存在)仍然是堆,故可重複上述的調整過程,對以R【large】為根的樹進行調整。此過程直至當前被調整的結點已滿足堆性質,或者該結點已是葉子為止。上述過程就象過篩子一樣,把較小的關鍵字逐層篩下去,而將較大的關鍵字逐層選上來。因此,有人將此方法稱為"篩選法"。
算法實例:
#include<stdio.h>
#include<stdlib.h>
inline int LEFT(int i);
inline int RIGHT(int i);
inline int PATENT(int i);
void MAX_HEAPIFY(int A【】,int heap_size,int i);
void BUILD_MAX_HEAP(int A【】,int heap_size);
void HEAPSORT(int A【】,int heap_size);
void output(int A【】,int size);