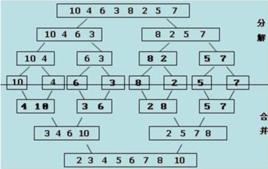
歸併操作
歸併操作(merge),也叫歸併算法,指的是將兩個順序序列合併成一個順序序列的方法。
如 設有數列{6,202,100,301,38,8,1}
初始狀態:6,202,100,301,38,8,1
第一次歸併後:{6,202},{100,301},{8,38},{1},比較次數:3;
第二次歸併後:{6,100,202,301},{1,8,38},比較次數:4;
第三次歸併後:{1,6,8,38,100,202,301},比較次數:4;
總的比較次數為:3+4+4=11;
逆序數為14;
算法描述
歸併操作的工作原理如下:
第一步:申請空間,使其大小為兩個已經排序序列之和,該空間用來存放合併後的序列
第二步:設定兩個指針,最初位置分別為兩個已經排序序列的起始位置
第三步:比較兩個指針所指向的元素,選擇相對小的元素放入到合併空間,並移動指針到下一位置
重複步驟3直到某一指針超出序列尾
將另一序列剩下的所有元素直接複製到合併序列尾
比較
歸併排序是穩定的排序.即相等的元素的順序不會改變.如輸入記錄 1(1) 3(2) 2(3) 2(4) 5(5) (括弧中是記錄的關鍵字)時輸出的 1(1) 2(3) 2(4) 3(2) 5(5) 中的2 和 2 是按輸入的順序.這對要排序數據包含多個信息而要按其中的某一個信息排序,要求其它信息儘量按輸入的順序排列時很重要。歸併排序的比較次數小於快速排序的比較次數,移動次數一般多於快速排序的移動次數。
用途
排序
(速度僅次於快速排序,為穩定排序算法,一般用於對總體無序,但是各子項相對有序的數列,套用見2011年普及複賽第3題“瑞士輪”的標程)
求逆序對數
具體思路是,在歸併的過程中計算每個小區間的逆序對數,進而計算出大區間的逆序對數(也可以用樹狀數組來求解)
scala代碼:
示例代碼
歸併排序原理
歸併排序具體工作原理如下(假設序列共有n個元素):
將序列每相鄰兩個數字進行歸併操作(merge),形成floor(n/2+n%2)個序列,排序後每個序列包含兩個元素
將上述序列再次歸併,形成floor(n/4)個序列,每個序列包含四個元素
重複步驟2,直到所有元素排序完畢
示例代碼
Swift語言
Go語言
Java語言
C#語言
Python語言
C語言
PHP語言
Pascal語言
Basic語言
JavaScript語言
使用遞歸的代碼如下。優點是描述算法過程思路清晰,缺點是使用遞歸,mergeSort()函式頻繁地自我調用。長度為n的數組最終會調用mergeSort()函式 2n-1次,這意味著一個長度超過1500的數組會在Firefox上發生棧溢出錯誤。可以考慮使用疊代來實現同樣的功能。
非遞歸算法(C++)
二路歸併
Delphi
歸併排序完整原始碼例子:
複雜度
歸併排序比較占用記憶體,但卻是一種效率高且穩定的算法。
改進歸併排序在歸併時先判斷前段序列的最大值與後段序列最小值的關係再確定是否進行複製比較。如果前段序列的最大值小於等於後段序列最小值,則說明序列可以直接形成一段有序序列不需要再歸併,反之則需要。所以在序列本身有序的情況下時間複雜度可以降至O( n)
TimSort可以說是歸併排序的終極最佳化版本,主要思想就是檢測序列中的天然有序子段(若檢測到嚴格降序子段則翻轉序列為升序子段)。在最好情況下無論升序還是降序都可以使時間複雜度降至為O( n),具有很強的自適應性。
| 最好時間複雜度 | 最壞時間複雜度 | 平均時間複雜度 | 空間複雜度 | 穩定性 | |
| 傳統歸併排序 | O(nlogn) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
| 改進歸併排序 | O(n) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
| TimSort | O(n) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
註:文獻 是一種改進的原地歸併算法,空間複雜度為O(1)。在表格里的改進歸併排序只是引入其預先判斷的這一步,這樣便可使傳統歸併排序時間複雜度降至O( n)。
歸併算法
定義
所謂歸併排序是指將兩個或兩個以上有序的數列(或有序表),合併成一個仍然有序的數列(或有序表)。這樣的排序方法經常用於多個有序的數據檔案歸併成一個有序的數據檔案。歸併排序的算法比較簡單。
基本思想方法:
(1)假設已經有兩個有序數列,分別存放在兩個數組s,r中;並設i,j分別為指向數組的第一個單元的下標;s有n個元素,r有m個元素。
(2)再另設一個數組a,k指向該數組的第一個單元下標。
(3)算法分析(過程):
完整的C++原始碼
歸併排序的實現方法:
1.自底向上算法
2.自頂向下
套用實例
NOIP2013 提高組火柴排隊