基本思想
設A是一個確定性算法,當它的輸入實例為x時所需的計算時間記為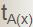 。設Xn是算法A的輸入規模為n的實例的全體,則當問題的輸入規模為n時,算法A所需的平均時間為
。設Xn是算法A的輸入規模為n的實例的全體,則當問題的輸入規模為n時,算法A所需的平均時間為
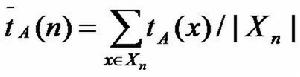
這顯然不能排除存在x∈Xn使得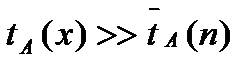 的可能性。希望獲得一個隨機化算法B,使得對問題的輸入規模為n的每一個實例均有
的可能性。希望獲得一個隨機化算法B,使得對問題的輸入規模為n的每一個實例均有
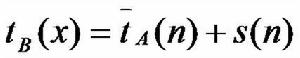
這就是舍伍德算法設計的基本思想。當s(n)與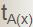 相比可忽略時,舍伍德算法可獲得很好的平均性能。
相比可忽略時,舍伍德算法可獲得很好的平均性能。
Sherwood算法的子集
Sherwood算法同類:
(1)線性時間選擇算法
(2)快速排序算法
有時也會遇到這樣的情況,即所給的確定性算法無法直接改造成舍伍德型算法。此時可藉助於隨機預處理技術,不改變原有的確定性算法,僅對其輸入進行隨機洗牌,同樣可收到舍伍德算法的效果。例如,對於確定性選擇算法,可以用下面的洗牌算法shuffle將數組a中元素隨機排列,然後用確定性選擇算法求解。這樣做所收到的效果與舍伍德型算法的效果是一樣的。
template<class Type>void Shuffle(Type a[],int n){ // 隨機洗牌算法 static RandomNumber rnd ; for(int i=0;i<n;i++) { int j=rnd.Random(n-i)+i ; Swap(a[i],a[j]); }}>跳躍表
1.舍伍德型算法的設計思想還可用於設計高效的數據結構。
2.如果用有序鍊表來表示一個含有n個元素的有序集S,則在最壞情況下,搜尋S中一個元素需要Ω(n)計算時間。
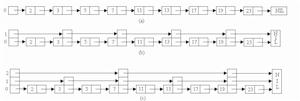
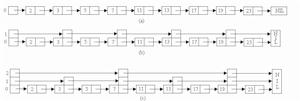
3.提高有序鍊表效率的一個技巧是在有序鍊表的部分結點處增設附加指針以提高其搜尋性能。在增設附加指針的有序鍊表中搜尋一個元素時,可藉助於附加指針跳過鍊表中若干結點,加快搜尋速度。這種增加了向前附加指針的有序鍊表稱為跳躍表。
4.應在跳躍表的哪些結點增加附加指針以及在該結點處應增加多少指針完全採用隨機化方法來確定。這使得跳躍表可在O(logn)平均時間內支持關於有序集的搜尋、插入和刪除等運算。
 舍伍德算法
舍伍德算法在一般情況下,給定一個含有n個元素的有序鍊表,可以將它改造成一個完全跳躍表,使得每一個k級結點含有k+1個指針,分別跳過
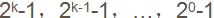 舍伍德算法
舍伍德算法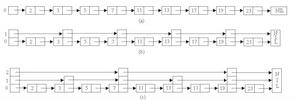 舍伍德算法
舍伍德算法完全跳躍表與完全二叉搜尋樹的情形非常類似。它雖然可以有效地支持成員搜尋運算,但不適應於集合動態變化的情況。集合元素的插入和刪除運算會破壞完全跳躍表原有的平衡狀態,影響後繼元素搜尋的效率。
為了在動態變化中維持跳躍表中附加指針的平衡性,必須使跳躍表中k級結點數維持在總結點數的一定比例範圍內。注意到在一個完全跳躍表中,50%的指針是0級指針;25%的指針是1級指針;…;
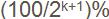 舍伍德算法
舍伍德算法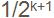 舍伍德算法
舍伍德算法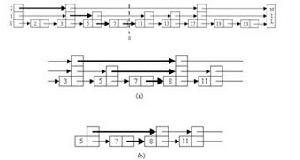 舍伍德算法
舍伍德算法在一個完全跳躍表中,具有i級指針的結點中有一半同時具有i+1級指針。為了維持跳躍表的平衡性,可以事先確定一個實數0<p<1,並要求在跳躍表中維持在具有i級指針的結點中同時具有i+1級指針的結點所占比例約為p。為此目的,在插入一個新結點時,先將其結點級別初始化為0,然後用隨機數生成器反覆地產生一個[0,1]間的隨機實數q。如果q<p,則使新結點級別增加1,直至q≥p。由此產生新結點級別的過程可知,所產生的新結點的級別為0的機率為1-p,級別為1的機率為p(1-p),…,級別為i的機率為
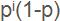 舍伍德算法
舍伍德算法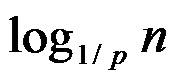 舍伍德算法
舍伍德算法經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科,就像一個人的思維能力一樣,其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展,新的算法也隨著新的套用漸漸出現,但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典,本任務就是要介紹這些經典算法。 |