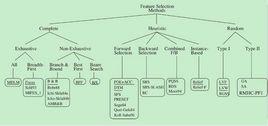
運算原理
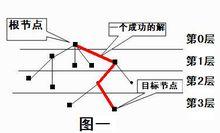 搜尋樹模型
搜尋樹模型搜尋算法實際上是根據初始條件和擴展規則構造一棵“解答樹”並尋找符合目標狀態的節點的過程。所有的搜尋算法從最終的算法實現上來看,都可以劃分成兩個部分——控制結構(擴展節點的方式)和產生系統(擴展節點),而所有的算法最佳化和改進主要都是通過修改其控制結構來完成的。其實,在這樣的思考過程中,我們已經不知不覺地將一個具體的問題抽象成了一個圖論的模型——樹,即搜尋算法的使用第一步在於搜尋樹的建立。
由圖一可以知道,這樣形成的一棵樹叫搜尋樹。初始狀態對應著根節點,目標狀態對應著目標結點。排在前的結點叫父結點,其後的結點叫子結點,同一層中的結點是兄弟結點,由父結點產生子結點叫擴展。完成搜尋的過程就是找到一條從根結點到目標結點的路徑,找出一個最優的解。這種搜尋算法的實現類似於圖或樹的遍歷,通常可以有兩種不同的實現方法,即 深度優先搜尋 (DFS——Depth First search)和 廣度優先搜尋 (BFS——Breadth First Search)。
主要分類
深度優先搜尋
如算法名稱那樣,深度優先搜尋所遵循的搜尋策略是儘可能“深”地搜尋樹。它的基本思想是:為了求得問題的解,先選擇某一種可能情況向前(子結點)探索,在探索過程中,一旦發現原來的選擇不符合要求,就回溯至父親結點重新選擇另一結點,繼續向前探索,如此反覆進行,直至求得最優解。深度優先搜尋的實現方式可以採用遞歸或者棧來實現。由此可見,把通常問題轉化為樹的問題是至關重要的一步,完成了樹的轉換基本完成了問題求解。
(1)減少節點數,思想:儘可能減少生成的節點數
(2)定製回溯邊界,思想:定製回溯邊界條件,剪掉不可能得到最優解的子樹
在很多情況下,我們已經找到了一組比較好的解。但是計算機仍然會義無返顧地去搜尋比它更“劣”的其他解,搜尋到後也只能回溯。為了避免出現這種情況,我們需要靈活地去定製回溯搜尋的邊界。
在深度優先搜尋的過程當中,往往有很多走不通的“死路”。假如我們把這些“死路”排除在外,不是可以節省很多的時間嗎?打一個比方,前面有一個路徑,別人已經提示:“這是死路,肯定不通”,而你的程式仍然很“執著”地要繼續朝這個方向走,走到頭來才發現,別人的提示是正確的。這樣,浪費了很多的時間。針對這種情況,我們可以把“死路”給標記一下不走,就可以得到更高的搜尋效率。
廣度優先搜尋
類似樹的按層遍歷,其過程為:首先訪問初始點Vi,並將其標記為已訪問過,接著訪問Vi的所有未被訪問過可到達的鄰接點Vi1、Vi2……Vit,並均標記為已訪問過,然後再按照Vi1、Vi2……Vit的次序,訪問每一個頂點的所有未被訪問過的鄰接點,並均標記為已訪問過,依此類推,直到圖中所有和初始點Vi有路徑相通的頂點都被訪問過為止。
對於狀態數很多時,廣度優先搜尋可以採用循環佇列或動態鍊表來處理,對於這兩種搜尋算法,其主要區別如下表:
| 遍歷方式 | 深度優先搜尋遍歷 | 廣度優先搜尋遍歷 |
| 所用數據結構 | 棧 | 佇列 |
| 一般最佳化 | 最優性剪枝 可行性剪枝 | Hash判重 雙向搜尋 |
雙向廣度優先搜尋
在廣度優先搜尋的基礎上進行最佳化,採用雙向搜尋的方式,即從起始節點向目標節點方向搜尋,同時從目標節點向起始節點方向搜尋。
特點:1.雙向搜尋只能用於廣度優先搜尋中。
2.雙向搜尋擴展的節點數量要比單向少的多。
A*算法
A*算法是利用問題的規則和特點來制定一些啟發規則,由此來改變節點的擴展順序,將最有希望擴展出最優解的節點優先擴展,使得儘快找到最優解。
對每一個節點,有一個估價函式F來估算起始節點經過該節點到達目標節點的最佳路徑的代價。
每個節點擴展的時候,總是選擇具有最小的F的節點。
F=G+B×H:G為從起始節點到當前節點的實際代價,已經算出,H為從該節點到目標節點的最優路徑的估計代價。F要單調遞增。
B最好隨著搜尋深度成反比變化,在搜尋深度淺的地方,主要讓搜尋依靠啟發信息,儘快的逼近目標,而當搜尋深的時候,逐漸變成廣度優先搜尋。
散列函式
散列函式(或散列算法,又稱哈希函式,英語:Hash Function)是一種從任何一種數據中創建小的數字“指紋”的方法。散列函式把訊息或數據壓縮成摘要,使得數據量變小,將數據的格式固定下來。該函式將數據打亂混合,重新創建一個叫做散列值(hash values,hash codes,hash sums,或hashes)的指紋。散列值通常用一個短的隨機字母和數字組成的字元串來代表。好的散列函式在輸入域中很少出現散列衝突。在散列表和數據處理中,不抑制衝突來區別數據,會使得資料庫記錄更難找到。
Rabin-Karp字元串搜尋算法是一個相對快速的字元串搜尋算法,它所需要的平均搜尋時間是O(n).這個算法是創建在使用散列來比較字元串的基礎上的。
最佳化
利用回溯算法進行最佳化:回溯和深度優先相似,不同之處在於對一個節點擴展的時候,並不將所有的子節點擴展出來,而只擴展其中的一個。因而具有盲目性,但記憶體占用少。
在搜尋中的最佳化:1.在搜尋前,根據條件降低搜尋規模。2.廣度優先搜尋中,被處理過的節點,充分釋放空間。3.給據問題的約束條件進行剪枝。
在剪枝時應遵循以下原則:
(1)正確性:剪去的“枝條”不包含最優答案;
我們知道,剪枝方法之所以能夠最佳化程式的執行效率,是因為它能夠“剪去”搜尋樹中的一些“枝條”。然而,如果在剪枝的時候,將“長有”我們所需要的解的枝條也剪掉了,那么,一切最佳化也就都失去了意義。所以,對剪枝的第一個要求就是正確性,即必須保證不丟失正確的結果,這是剪枝最佳化的前提。
為了滿足這個原則,計算機應當利用“必要條件”來進行剪枝判斷。也就是說,通過解所必須具備的特徵、必須滿足的條件等方面來考察待判斷的枝條能否被剪枝。這樣就可以保證所剪掉的枝條一定不是正解所在的枝條。當然,由必要條件的定義,沒有被剪枝不意味著一定可以得到正解(否則,也就不必搜尋了)。
(2)準確性:在保證第一條原則的情況下,儘可能的剪去更多不包含最優答案的枝條;
在保證了正確性的基礎上,對剪枝判斷的第二個要求就是準確性,即能夠儘可能多的剪去不能通向正解的枝條。剪枝方法只有在具有了較高的準確性的時候,才能真正收到最佳化的效果。因此,準確性可以說是剪枝最佳化的生命。
(3)高效性:通過剪枝要能夠更快的接近到達最優解。
一般說來,設計好剪枝判斷方法之後,我們對搜尋樹的每個枝條都要執行一次判斷操作。然而,由於是利用出解的“必要條件”進行判斷,所以,必然有很多不含正解的枝條沒有被剪枝。這些情況下的剪枝判斷操作,對於程式的效率的提高無疑是具有副作用的。為了儘量減少剪枝判斷的副作用,我們除了要下功夫改善判斷的準確性外,經常還需要提高判斷操作本身的時間效率。
然而這就帶來了一個矛盾:我們為了加強最佳化的效果,就必須提高剪枝判斷的準確性,因此,常常不得不提高判斷操作的複雜度,也就同時降低了剪枝判斷的時間效率;但是,如果剪枝判斷的時間消耗過多,就有可能減小、甚至完全抵消提高判斷準確性所能帶來的最佳化效果,這恐怕也是得不償失。很多情況下,能否較好的解決這個矛盾,往往成為搜尋算法最佳化的關鍵。
套用案例
(1)題目:黑白棋遊戲
黑白棋遊戲的棋盤由4×4方格陣列構成。棋盤的每一方格中放有1枚棋子,共有8枚白棋子和8枚黑棋子。這16枚棋子的每一种放置方案都構成一個遊戲狀態。在棋盤上擁有1條公共邊的2個方格稱為相鄰方格。一個方格最多可有4個相鄰方格。在玩黑白棋遊戲時,每一步可將任何2個相鄰方格中棋子互換位置。對於給定的初始遊戲狀態和目標遊戲狀態,編程計算從初始遊戲狀態變化到目標遊戲狀態的最短著棋序列。
(2)分析
這題我們可以想到用深度優先搜尋來做,但是如果下一步出現了以前的狀態怎么辦?直接判斷時間複雜度的可能會有點大,這題的最優解法是用廣度優先搜尋來做。我們就可以有初始狀態按照廣度優先搜尋遍歷來擴展每一個點,這樣到達目標狀態的步數一定是最優的(步數的增加時單調的)。但問題是如果出現了重複的情況我們就必須要判重,但是樸素的判重是可以達到狀態數級別的,其實我們可以考慮用hash表來判重。
Hash表:思路是根據關鍵碼值進行直接訪問。也就是說把一個關鍵碼值映射到表中的一個位置來訪問記錄的過程。在Hash表中,一般插入,查找的時間複雜度可以在O(1)的時間複雜度內搞定。對於這一題我們可以用二進制值表示其hash值,最多2^16次方,所以我們開個2^16次方的表記錄這個狀態出現沒有,這樣可以在O(1)的時間複雜度內解決判重問題。
 搜尋算法
搜尋算法進一步考慮:從初始狀態到目標狀態,必定會產生很多無用的狀態,那還有什麼最佳化可以減少這時間複雜度?我們可以考慮把初始狀態和目標狀態一起擴展,這樣如果初始狀態的某個被擴展的點與目標狀態所擴展的點相同時,那這兩個點不用擴展下去,而兩個擴展的步數和也就是答案。
上面的想法是雙向廣度優先搜尋:
就像圖二一樣,多擴展了很多不必要的狀態。
從上面一題可以看到我們用到了兩種最佳化方法,即 Hash表最佳化和 雙向廣搜最佳化。一般的廣度優先搜尋用這兩個最佳化就足以解決。
經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科,就像一個人的思維能力一樣,其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展,新的算法也隨著新的套用漸漸出現,但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典,本任務就是要介紹這些經典算法。 |